NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/07/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	EXPOSANTS
Débutants Général	RACINES 13^e				Glossaire Général
INDEX Racine Calcul mental	Règles de base =>	Principe	Unités et dizaines	Poids forts
	2 chiffres =>	Dizaine impaire	Dizaine paire
		Sommaire de cette page >>> Approche >>> Principe n°1 – Unité >>> Principe n°2 – Dizaine >>> Nombres en …1 >>> Nombres en …7 >>> Nombres en …3 >>> Nombres en …9

RACINE TREIZIÈME

Technique de base du calcul

des unités et des dizaines

Nous nous limiterons ici aux racines à deux chiffres, soit aux puissances jusqu'à 100¹³.

Voici deux règles bien utiles.

Principe de base N°1 - Unité

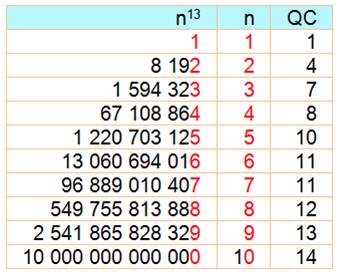
Tous les nombres à la puissance 5, 9, 13 ou 17 (soit en n = 4k + 1) ont même unité que le nombre lui-même. Par exemple: 2^13 = 8 192, 3^13 = 1 594 323, 4^13 = 67108864. Les puissances 4k+1 d'un nombre reproduit son unité: Voir Chiffres des unités des puissances Or 13 est le premier nombre à deux chiffres dans ce cas. Ce qui le rend impressionnant pour le grand public par rapport à la racine cinquième ou même la racine neuvième qui serait tout de même de grands défis. Table des puissances 13 des nombres de 1 à 10 QC est la quantité de chiffres Règle n°1 L'unité de la racine treizième est celle du nombre donné. Exemple pour un défi sur les dix premiers Racine treizième de 549 755 813 888 Sachant qu'il s'agit d'un nombre de 1 à 10 je donne immédiatement 8.

Principe de base N°2

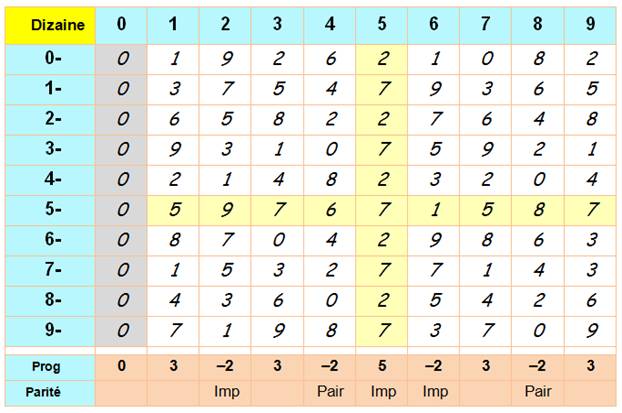
Le constat s'applique au chiffre des dizaines. La propriété n'est pas évidente à dégager. Elle conclut à une progression arithmétique sur le chiffre des dizaines. Pour cela, examinons le chiffre des dizaines des puissances 13, listés par décades. Table des chiffres des dizaines des puissances 13 des nombres de 0 à 99 Exemple de lecture: le nombre 15^13 se termine par 75, le 7 lu dans cette table et le 5 des unités égal à celui du nombre donné. La colonne 0, les puissances de 10, est triviale. Dans la colonne 1, les nombres 1, 11, 21, 31 …, le chiffre des dizaines progresse de 3 en 3. Même constat pour toutes les colonnes avec des progressions de 3, –2, 5. Autre remarque, dans les colonnes paires, les chiffres sont de la même parité (conséquence de la progression avec un pas de 2). La colonne du 5, nombres terminés par 5, le chiffre des dizaines est 2 ou 7, seulement. Règle n°2 Le chiffre des dizaines de la puissance treizième est en progression arithmétique pour les nombres progressant de 10 en 10.

Bilan

Oui! Règle pas très utilisable telle quel. Une certaine gymnastique intellectuelle va être nécessaire pour l'appliquer. Pour cela, procédons par colonne du même type:

Impaires,

Paires et

Cas particulier du 5.

Suite	Calculs des poids forts
Voir	Racine cubique Racine cinquième
Site	Voir Liste
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/Racine13.htm