|
||||||||||||||||||||||||||||||||||||||||
![]()
|
RACINE TREIZIÈME Principe
du calcul Objet de calcul mental par
certains prodiges jusqu'à des nombres de 100 voire 200 chiffres. Quel est
leur secret ? Explorons quelques principes qui facilitent leur tâche tout en
reconnaissant que ces calculs relèvent néanmoins de l'exploit: mémoire et
agilité mentale. Calcul de la racine treizième d'un nombre
de 100 chiffres: Record 2002: Alexis Lemaire – 13,55 s Record 2004: Gert Mittring – 11,80 s (non homologué) Record 2004: Alexis Lemaire –
3,6 s (non homologué) En explorant ce sujet, nous allons faire appel à diverses techniques
de calcul. C'est le principal intérêt de ces pages. |
Anglais: Lightning calculators
|
Racine
89 247e d'un nombre d'un million de chiffres. Exploit réalisé en
6 minutes et 1,4 seconde par Gert Mittring à Zurich dont le QI est estimé à 175. |
Voir Actualités
2016
Actualité janvier 2014
|
Racine
13e de 13 060 694 016 = 6 Exploit réalisé en
une minute en janvier 2014 durant une émission de télévision par Zhou Wei, surnommé
le Rain Man chinois, du fait qu'il souffre de troubles mentaux |
Exercice simple
|
Défi Trouver
N13 = m Quelle
est la racine treizième de m, sachant qu'il s'agit d'un nombre entier ? |
m
= 981 4843037474 6156652212 8614150507 8084763648 = 9,81... 1042 |
|||
|
Ordre de grandeur Nombre
à 43 chiffres |
100013
= 1039 200013
= 213 × 1039 = 8192 ×
1039 = 8,192 1042 m
est légèrement supérieur à 2000 |
|||
|
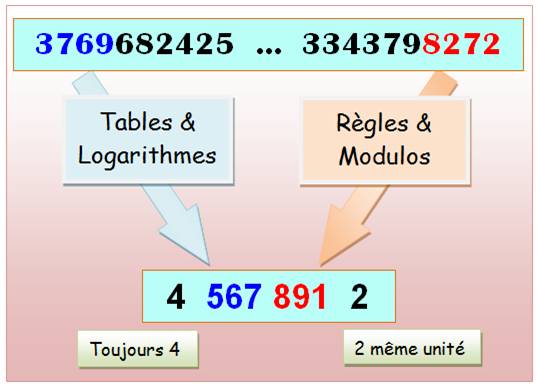
Unités = 8 On
établit le tableau des unités des puissances. Avec
1 et 2, on sait que l'on arrivera à 1 et à 2. Et pas 8. Avec
3, on a successivement 3×3 = 9, 9×3 = 27, on garde 7; puis 9×7
= 63, on garde 3; puis 7×3 = 21, on garde 1; etc. pour aboutir à 3
qui e convient pas. Seul
8 produit un 8 pour unité à la puissance 13. |
Table des unités
des puissances jusqu'à la puissance 13
Seul
le chiffre 8 convient pour les unités de N. |
|||
|
Solution |
N
= 2008 |
|||
|
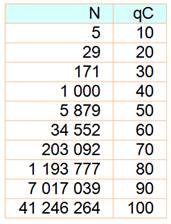
Vérification |
Table des
puissances de 8 avec unité, dizaines puis centaines
|
|||
|
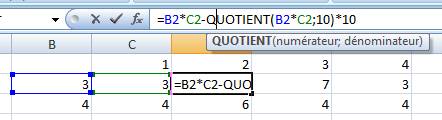
Méthode de calcul de l'unité On
cherche le quotient de la division par 10, qui supprime l'unité, et on
multiple pat 10. Ce
nombre est soustrait du nombre initial. |
Formule de calcul sur tableur
Exemple avec 7×3 = 21 => 21 – 2×10 = 1 |
|||
D'après Alon Amit – Février 2022
![]()
Plus généralement
|
|
|
|
Exemple
Il existe 7 992 563 racines treizièmes à cent chiffres.
le dernier chiffre est égal au dernier du nombre
proposé. Record du monde par Alexis Lemaire (1980-)
|
|
Voir Sites
Internet pour historique détaillé
|
|
|
|
|
|
|
|
|
|
1234513 = 1546 6221494091 4131102165
1977071012 9584923084 5947265625 avec 54 chiffres.
213 = 8192 avec 4 chiffres.
1013 = 1000 0000000000 avec 14 chiffres (13 + 1). 10013 = 1000000 0000000000 0000000000 avec 27 chiffres (2 x 13 + 1). 100013 = 1000000000
0000000000 0000000000 0000000000 avec 40 chiffres (3 x 13 + 1).
Encadrement par une puissance de 10 100 / 13 = 7,69… (107)13
=> 92 chiffres (7 x 13 + 1). (108)13
=> 105 chiffres (8 x 13 + 1). En fait:
Une recherche complète montre qu'il y a presque
50 millions de nombres (49 238 826) qui ont une puissance treizième avec au
plus 100 chiffres.
9999999162 8809505076 4468891852 4814522347 2426272392 4318937611
5437857450 7585909784 4482036507 4927230976
|
|
|
|
|
|
1. Description des techniques de base pour le calcul des poids faibles et
pour les poids forts. 2. Calcul de la racine en se limitant à 10013, soit une racine
avec deux chiffres seulement. Le calcul mental de tête pour un tel cas limité
reste un challenge. >>> 3. Description des méthodes permettant d'aborder la résolution générale
du problème à 100 chiffres: avec le bagage décrit dans ce site, se reporter
aux sites Internet spécialisés. |
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()