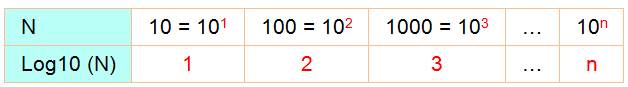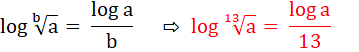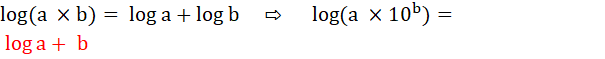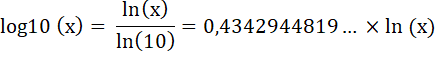racine treizième

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/07/2018 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	EXPOSANTS
Débutants Général	RACINES 13^e				Glossaire Général
INDEX Racine Calcul mental	*Règles de base =>*	Principe	Unités, dizaines …	Poids forts
	*2 chiffres =>*	Dizaine impaire	Dizaine paire
		Sommaire de cette page >>> Principe de calcul >>> Rappels sur les logarithmes >>> Racine 13^e avec les logs >>> Principe du calcul – Racines 13^e / 100 chiffres

RACINE TREIZIÈME

Technique de base du calcul

des poids forts

Principe de calcul des chiffres de poids forts (ceux de gauche dans le nombre). On procède selon deux techniques:

Calcul de l'ordre de grandeur pour les petites racines (Voir exemple avec les racines cubiques)

Calcul en passant par les logarithmes pour le cas général, notamment la racine treizième.

Principe de calcul

Dans le monde des logarithmes, la racine 13^e devient une division par 13. Plus simple, à deux conditions:

effectuer une division par 13, ce qui nécessite un certain entraînement; et

connaître un certain nombre de logarithmes par cœur.

Partant du nombre N (ou de ses chiffres de poids fort, comme nous le verrons plus loin)

calcul du log base 10 de N;

division par 13; et

calcul de l'antilog de ce résultat qui donne immédiatement la racine R.

Rappels sur les logarithmes

Pour les calculs, nous utilisons les logarithmes en base 10 (abrégés en log) et non les logarithmes népériens à base e (ln).

Exemples

Puissances de 10: le logarithme est simplement l'exposant de la puissance.

Formules

Log et antilog

Passage du log au ln

Calcul de l'antilog

avec ln (10) = 2,302585093…

Exemple: log (123456789) = 8,091514979…

antilog (8,091514979) = exp(8,0915 x 2,302585093) = 123456789,5

En pratique

Ces calculs ne peuvent être effectués qu'avec l'aide d'une calculette ou d'un tableur. Pour le calcul mental de la racine treizième, une table, aussi limitée que possible, est mémorisée. Les calculs se font par interpolation à partir des valeurs de la table.

Racine 13^e avec les logs
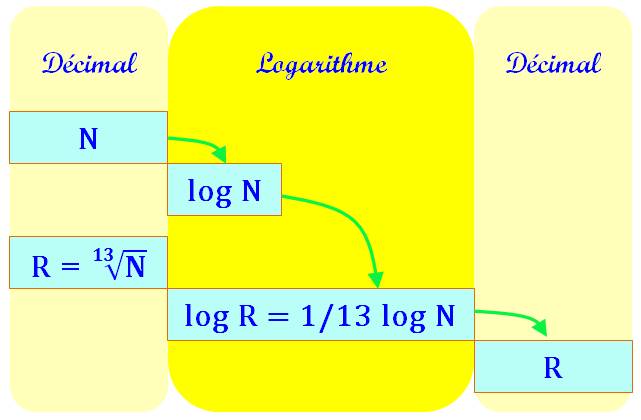
Décimal entrée	Calculs avec log	Décimal sortie
Exemple
N = 877521 0229989679 8785221299 Quantité de chiffres: 26	log10 (N) = 25 + log10 (8,77) = 25 + 0,94325… = 25,94325…	NB: On sait que N est bien un cube parfait.
	log10 () = 1/13 x log10(N) = 25,94325…/13 = 1,9956…	= 10^1,9956… = 98,99 => 99 Confirmé par l'unité en 9.
Maximum
N = 10¹⁰⁰ (qC = 101)	log10 (N) = 100	NB: N n'est pas un cube parfait.
	log10 () = 1/13 x log10(N) = 100 / 13 = 7,6923…	= 10^7,6923… = 4,923795420 … 10⁷ = 49 237 954,20

Principe du calcul – Racines 13^e de nombres à100 chiffres
Pour obtenir un calcul mental des poids forts, il est possible d'utiliser les logarithmes. Une autre méthode consiste à mémoriser quelques valeurs et a effectuer les corrections nécessaires par interpolation. Voici la table proposée par Ron Doerfler and Miles Forster. Elle comporte neuf triplets de valeurs, nombres en gras. La méthode à l'œuvre N = 2928811583 4875201060 5535673527 8365212219 6502020937 1392842551 0086152669 6334642225 8777030827 9739304053 dont nous connaissons la racine R = 4480 0613.
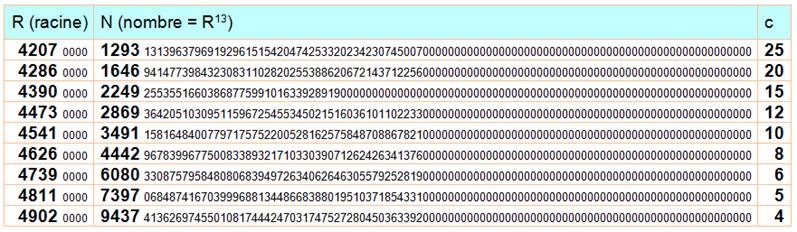
Cinq premiers chiffres Le plus proche dans la table Écart / 100 Correction (cf. table)	2928,8 2869 0059,8 / 100 = 0,598 0,6 0,6 x 12 = 7,2
Racine lue dans la table / 100 Correction Somme Quatre premiers chiffres	4473 7,2 4480,2 4480
Il s'agit là du principe. Parfois, il est nécessaire d'introduire des corrections du second ordre.

Suite	Deux chiffres – Dizaine impaire
Voir	Racine cubique Racine cinquième
Sites	Voir Liste
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/Racine13.htm