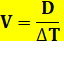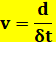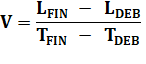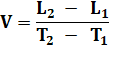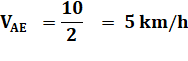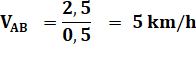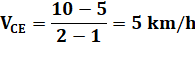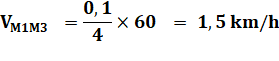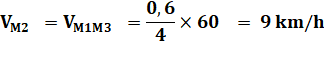|
|||||||||||||||||||||||||||||||||
![]()
|
Notion de vitesse Spécial débutants (page
2/2) Dés que l'on parle de
vitesse, je suis perdu; je n'y comprends rien. Pourtant quelques bases
simples et tout devient plus facile… |
|
|
|
Vitesse
– Toutes ces formules sont identiques!!! Ce sont les notations qui changent |
|
||
|
|
L est la longueur parcourue
durant le temps T. Ex: 500 km = 100 km/h x 5 heures |
||
|
Pour trouver
cette nouvelle relation, je divise
chaque membre de la relation précédente par T. C'est vrai, je
peux? Mais oui! Comme
en algèbre. Même en physique, les maths ça sert. |
Ex: 100 km/h = 500 km / 5 heures Facile à retenir: pensez à
la voiture dont la vitesse s'exprime en kilomètres
par heure. C'est bien la distance qu'il faut diviser par le temps. On aura aussi bien:
|
||
|
|
|
||
|
Ex: Je pars du bureau qui est à 10 km de chez moi à 18h et j'arrive à la
gym qui est à 5 km de chez moi à 18h15. Quelle est ma vitesse? V = (10km – 5km) / (18h15 –
18h) =
5km / 0,25h = 20 km/h Il s'agit
d'une vitesse moyenne. j'ai pu courir ou me reposer, mais au bilan, j'ai bine
parcouru 20 km en une heure. On dit qu'il s'agit d'une vitesse moyenne. |
ou
ou …
toutes autres notations convenues. |
||
Voir Fractions
|
La
vitesse est exprimée en m/s dans le système SI. Correspondance
entre km/h et m/s 1 km / h = 1000 m / 3600 s =
0,2777… m / s 1 m / s = 1 / 0,2777… = 3,6 km
/ h Notez que km s'écrit en lettres minuscules. |
Voir Unités de vitesse
|
|
||
|
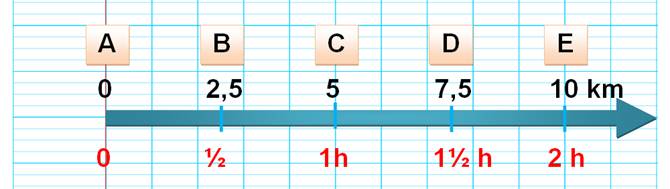
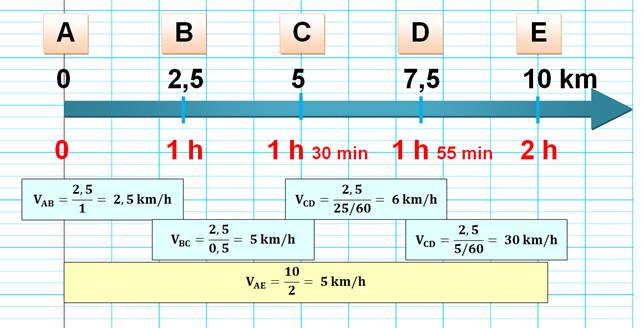
Exemple
1
|
||
|
Vitesse moyenne entre A et E Vitesse moyenne entre A et B Vitesse moyenne entre C et E |
|
|
|
Exemple
2
|
||
|
|
||
|
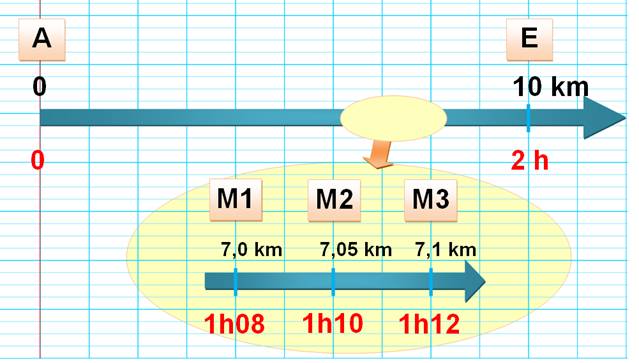
Exemple
3
|
||
|
Vitesse moyenne entre M1 et M3 Soit 0,1 km en 4 minutes: |
|
|
|
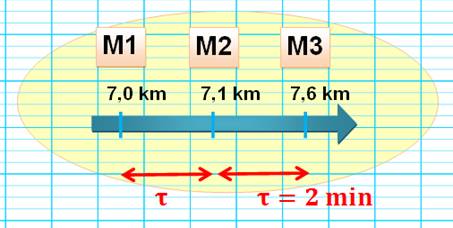
Exemple
4
|
||
|
Vitesse instantanée en M2 |
|
|
Bilan
|
La
vitesse de la voiture est donnée en
kilomètre par heure. Je divise la distance parcourue par le temps. La
vitesse moyenne est calculée divisant la distance
totale et la durée totale sur le parcours. La
vitesse instantanée en un point est la
vitesse moyenne sur un tout petit intervalle de part et d'autre du point (voir dérivée). |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |