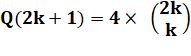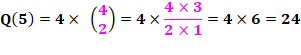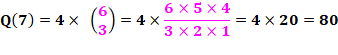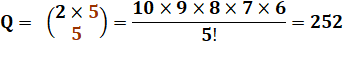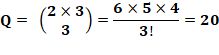Abracadabra et Mississippi en carrés

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/06/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Dénombrement
Débutants Dénombrement	Études de cas				Glossaire Général
INDEX Dénombrement Vue globale Jeux de nombres Énigmes	Mississippi	Quart de finale		Oiseaux
	Boules de couleur		Abracadabra et Mississippi
	Lettres en contact
		Sommaire de cette page >>> Approche >>> TRIANGLE-Diagonales >>> CARRÉ-Diagonales – 3 lettres >>> CARRÉ-Diagonales – k lettres >>> CARRÉ-Droit >>> Losange - Abracadabra

ABRACADABRA & MISSISSIPPI

en triangles et en carrés

Jeux avec des lettres disposées en grilles. Le cas des lettres disposés en carrés est traité sur la page mots carrés ou mots en grilles.

Sur cette page, comparaison entre dispositions droites ou en diagonales.

Avec les diagonales, le dénombrement implique les puissances de 2, et

Avec la disposition droite, le dénombrement implique le triangle de Pascal.

Approche
Les jeux de grilles sont populaires, voire parfois ésotériques. Rares sont les sites abordant le problème du dénombrement. Petite revue.
Abracadabra et magie Ici, le mot magique "abracadabra" ou "abrakadabra" est inscrit sur chaque ligne Il est tronqué pour donner cette forme de triangle. Aujourd'hui utilisé par les magiciens, il représentait jadis une sorte de talisman. Comme jeu de grille, ce modèle en triangle ne présente pas grand intérêt. Le mot ne peut être écrit que deux fois: ligne du haut et côté droit, en remontant. Le mot semble symétrique (palindrome), mais ne l'est pas.
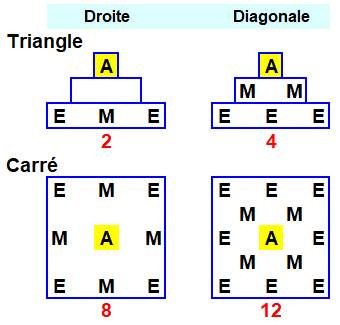
Quatre configurations Grilles droites ou diagonales Format triangle ou carré; voir aussi le losange. Ici, avec trois lettres (AME). Avec ces exemples simples, on constate la variété des dénombrements (2, 4, 8 ou 12). Chaque lecture est appelée un mot, chacun représenté par un chemin sur la grille. Le chemin part d'une lettre origine, dite pivot, et se dirige vers la lettre suivante: parcours droit (horizontal ou vertical) pour les uns ou parcours en oblique pour les autres.

TRIANGLE-Diagonales

Les lettres sont placées sur une grille en triangle. Une lettre nouvelle pour chaque ligne.

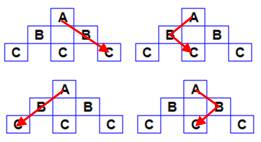
Combien de fois la suite de lettres (mots)?

Trois lettres

Avec A, se présentent deux directions, puis même chose avec B.

Total: 2 x 2 = 4 fois ABC.

Note importante: du fait de l'écriture des lettres par lignes, les trajets en rouge sont toujours descendants.

		A
	B		B
C		C		C

Quatre lettres

Le même type de décompte conduit à:
2 x 2 x 2 = 8 fois ABCD.

Total: T(4) = 2³ mots

Cinq lettres

Le même type de décompte conduit à:
2 x 2 x 2 x 2 = 16 fois ABCDE.

Total: T(5) = 2⁴ mots

k lettres

Total: T(k) = 2^{k – 1} mots

				A
			B		B
		C		C		C
	D		D		D		D

				A
			B		B
		C		C		C
	D		D		D		D
E		E		E		E		E

Cas typiques

T(9) = 2⁸ = 256

T(11) = 2¹⁰ = 1024

T(15) = 2¹⁴ = 16 384

T(20) = 2¹⁹ = 524 288

AGAMEMNON

MISSISSIPPI

ABRACADABRA

DEMOCRATISATION

DÉSOXYRIBONUCLÉIQUES

CARRÉ-Diagonales – 3 lettres

Pour former le carré à partir du triangle, on commence par ajouter les lettres en rouge.

On a deux fois le triangle précédent: 2 x 4 mots,
sauf le mot en jaune qui est commun au deux triangles.

Total : 2 x 2² – 1 = 7 mots

Avec le troisième quadrant, on ajouté à nouveau un triangle initial (4 mots), sauf un en commun.

Total: 3 x 2² – 2 = 10

Avec le quatrième quadrant, on ajouté à nouveau un triangle initial (4 mots), sauf deux en commun. En fait, seulement deux chemins en plus pour atteindre le C du haut au centre.

Total: 4 x 2² – 4 = 12

Un dessin des trajets montre le décompte

4 chemins rouges;

4 x 2 = 4 chemins vert;

Total: 12.

				C
			B
		A		C
	B		B
C		C		C

C				C
	B		B
C		A		C
	B		B
C		C		C

C		C		C
	B		B
C		A		C
	B		B
C		C		C

CARRÉ-Diagonales – k lettres

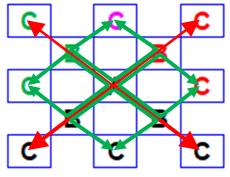
Quatre lettres

Avec le même décompte que précédemment, on aurait:

4 fois le cas du triangle à quatre lettres, soit 4 x 2³ = 32 mots;

4 fois les rayons rouges en double;

Total = 32 – 4 = 28 mots.

Un dessin des trajets vérifie le décompte:

4 chemins rouges;

8 chemins verts;

8 chemins violets;

8 chemins ocre;

Total : 20 chemins.

Généralisation à k lettres

C(3) = 4 x 2² – 4 = 12

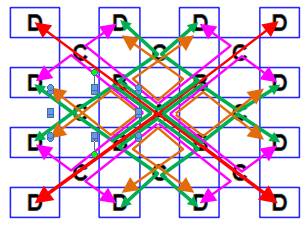
C(4) = 4 x 2³ – 4 = 28

C(k) = 4 x 2^k – 4

Note (Illustration du bas)

Il est important de remarquer que, sauf les rayons verts communs, tous les autres trajets se produisent dans leur propre secteur. Aucun ne vient empiéter le secteur voisin.

D'où le principe du dénombrement en quatre fois, moins les communs.

D		D		D		D
	C		C		C
D		B		B		D
	C		A		C
D		B		B		D
	C		C		C
D		D		D		D

CARRÉ-Droit

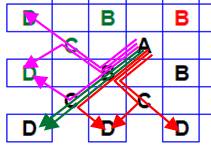
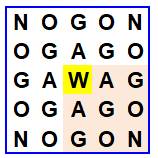
Carré 5 x 5

Ce cas est traité en détail sur la page mots carrés ou mots en grilles.

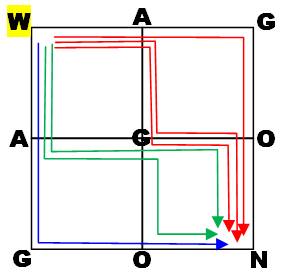
Chaque quadrant est indépendant. Aucun chemin en commun.

Avec les cinq lettres du mot WAGON, sur cette grille, on peut lire (3 + 2 + 1) = 6 mots par quadrant, soit 4 x 6 = 24 mots au total.

Décompte

Ayant choisi WA_H, il y a trois routes possibles (rouges);

Ayant choisi WA_V, il y a deux routes possibles (vertes);

Ayant choisi WG, il y a une route possible bleue).

Analogie avec les combinaisons

Choix de 2 lettres parmi 4 => AB, AC, AD // BC, BD // CD => 3 + 2 + 1 = 6 cas ou combinaisons de 2 parmi 4.

Formule générale pour 2 k + 1 lettres

Exemples

Carré complet avec le mot WAGON

Chemins dans un quadrant

Voir Triangle de Pascal – Table des valeurs

Voir Combinaisons

Losange - Abracadabra
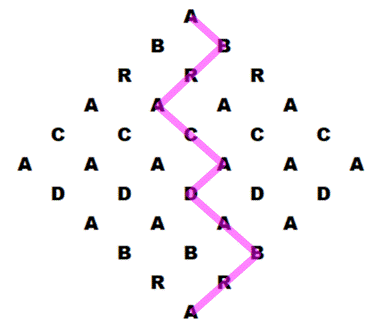
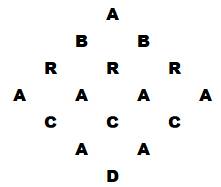
Le défi Le mot ABRACADABRA se prête bien à cette disposition en losange. Combien de fois ce mot dans ce losange ? Notes: Le chemin est toujours descendant malgré la présence de lettres identiques qui pourraient laisser penser qu'il existe des chemins latéraux ou remontant. Le losange est un artifice de présentation et on pourrait tout aussi bien faire pivoter la figure de 45 ° et retrouver la disposition en carré vue ci-dessus pour un quadrant seul.
Dénombrement Carré de six lettres de côté, soit 5 intervalles.
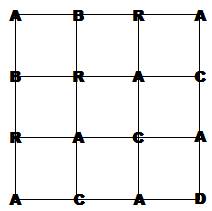
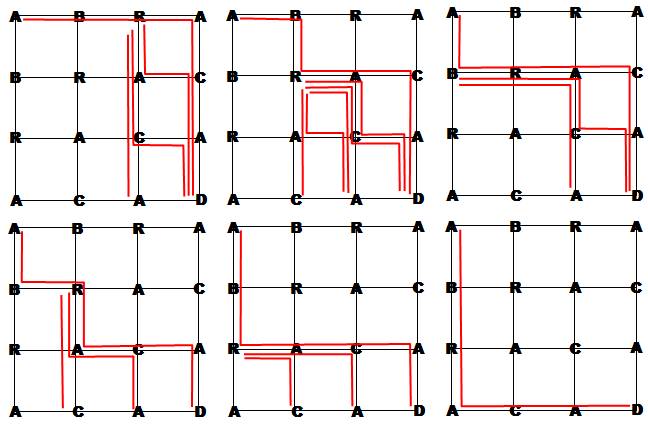
Vérification avec 8 lettres Le losange est converti en carré. Identifions les 20 chemins (ci-dessous)

Carré ABRACADABRA – 4 x 252 = 1008 fois le mot

Merci à Jérôme Mayer pour ses contibutions

Voir ses pages ABRADABRA et BONNE NOUVELLE

Voir	Mississipi – Anagrammes Mississippi en grille – Quantité de chemins Arrangements – Exemples Dénombrement – Index Trois dés et une urne Quantité de nombres avec les chiffres d'un nombre
Aussi	Coefficients multinomiaux États-Unis – Centre Jeux – Index
Site	Abracadabra – Wikipédia
Cette page	http://villemin.gerard.free.fr/Denombre/aaaCAS/Abraca.htm