NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/03/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Dénombrement
Débutants Dénombrement	Études de cas						Glossaire Général
INDEX Dénombrement Vue globale	Mississippi	Quart de finale			Oiseaux
	Boules de couleur			Abracadabra et Mississippi
	Lettres en contact		Bouquins			Pokémon
		Sommaire de cette page >>> 3 boules et 2 couleurs >>> 3 boules et 3 couleurs >>> 4 boules et 2 couleurs >>> n boules et k couleurs >>> Table pour n et k jusqu'à 10

Boules de différentes couleurs

Dénombrer les possibilités d'assortir n boules de k couleurs. Tous les cas sont possibles. Les boules peuvent être de couleurs identiques ou différentes.

Autres exemples: attribuer à n ouvriers une plage horaire parmi k. Prendre n bonbons pour n enfants dans k pots de bonbons différents.

3 boules et 2 couleurs
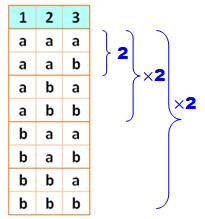
Chaque boule (1, 2, 3) peut prendre la couleur a ou b. On compte 2^3 = 8 possibilités. Le nombre 2 est dû à la quantité de couleurs et le nombre 3 à la quantité de boules.

3 boules et 3 couleurs
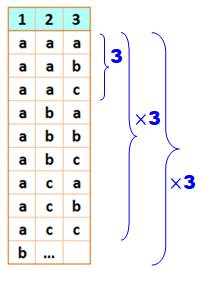
Chaque boule (1, 2, 3) peut prendre la couleur a, b ou c. On compte 3^3 = 27 possibilités. On retrouve la règle: nombre = quantité de couleur et exposant = quantité de boules.

4 boules et 2 couleurs
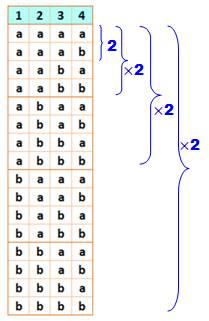
Chaque boule (1, 2, 3, 4) peut prendre la couleur a ou b. On compte 2^4 = 16 possibilités. Avec 4 boules et 3 couleurs, on aurait: 3^4 = 81 possibilités. Avec 4 boules et 4 couleurs, on aurait: 4^4 = 256 possibilités.

n boules et k couleurs
Avec n boules de k couleurs, on compte: Q = k^n Il s'agit de la formule pour une p-liste: avec ordre et avec remise. Exemple Supposez que vous ayez 10 ouvriers et 6 plages horaires. Quelles seront les possibilités d'affectation des plages aux ouvriers de toutes les manières possibles? Réponse: plus de 60 millions.	Avec n = 4 et k = 2: Q = 2^4 = 8 Avec n = 3 et k = 5: Q =5^3 = 125 Avec n = 10 et k = 6 : Q = 6^10 = 60 466 176

Table pour n boules de k couleurs de 1 à 10

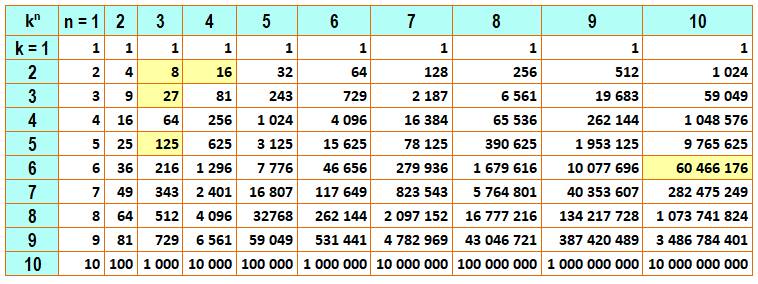
En jaune, les cas rencontrés sur cette page

Voir Table – Index

Voir	Panorama des dénombrements – p-liste avec remise Arrangements – Exemples Dénombrement – Index Trois dés et une urne
Aussi	Coefficients multinomiaux États-Unis – Centre Jeux – Index
Cette page	http://villemin.gerard.free.fr/Denombre/aaaCAS/Boules.htm