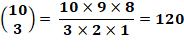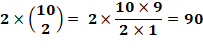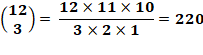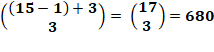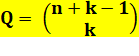|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
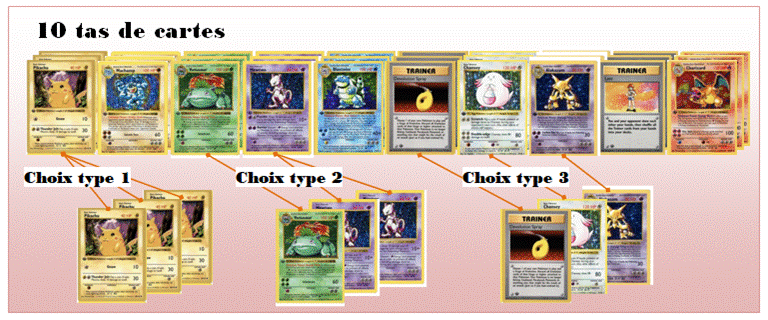
Choix de cartes sans ordre et avec répétition Dix tas de cartes Pokémon.
Chaque pile contient la même carte; ce qui veut dire que je peux en prendre
autant que je veux. Justement, ce petit garçon est
autorisé à en prendre trois. Combien de possibilités ?
|
|
|
||
|
Il s'agit
de choisir trois cartes parmi les celles des dix tas, chaque tas contenant la
même carte, et, on peut choisir plusieurs fois la même carte.. Trois
types de choix:
|
Si les cartes sont identiques, il prend dans le
tas n°2, n°2 … ou n°10. Soit 10 possibilités. Si les cartes sont toutes différentes, il s'agit
des combinaisons de 3 parmi 10. Si les deux cartes sont identiques, il s'agit des
combinaisons de 2 parmi 10 avec une répétition de 2 Bilan: 10 + 120 + 90 = 220 choix possibles. |
|
|
|
||
|
L'idée
consiste à placer une marque sur les cartes choisies et à dénombrer toutes
les possibilités de répartition des trois marques sur les dix tas, soit
treize objets. On note le
choix 111 par:
Ou le
choix 225 par
Ou encore
3,4, 8
|
Chaque choix de trois cartes correspond à une configuration
différente de ces objets. Observez que pour toutes les combinaisons le
premier rectangle est toujours là. Il n'y a que 13 – 1 = 12 objets à
considérer. Le calcul devient simplement:
Autre exemple: avec une glace trois boules et 15
parfums disponibles, la quantité de façons de composer une coupe est: |
|
|
Le nombre de manières de choisir
k objets parmi n, lorsque l'ordre n'est pas important et la répétition
possible, est égal à:
|
Glace 2
boules, 3 parfums: 6 types de cônes

{11, 22, 33, 12,
13, 23}
Voir Brève
603
![]()
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()