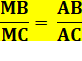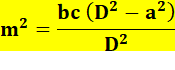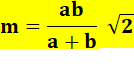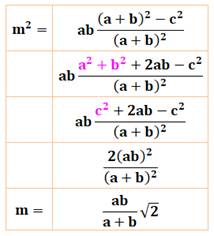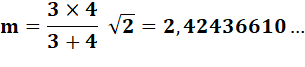|
Édition du: 04/12/2024 |
|
INDEX |
Bissectrice |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Théorème de la bissectrice
Calcul de
longueurs liées à la construction des bissectrices des angles dans le
triangle quelconque. Défis de la trisection
d'un angle dans un triangle rectangle (illustration). |
||
|
|
Sommaire de cette page >>> Bissectrices dans le triangle >>> Segments découpés >>> Longueur de la bissectrice >>> Défi des trois angles égaux |
Débutants Glossaire |
|
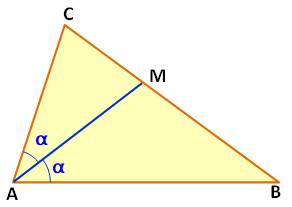
Théorème de la bissectrice Dans
le triangle quelconque, la bissectrice AM découpe une sécante BC dans le rapport des côtés
adjacents AB et AC.
Voir Démonstration |
|
|
|
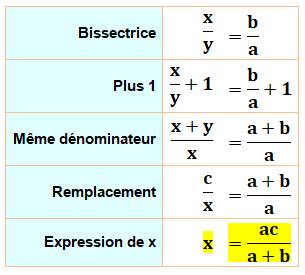
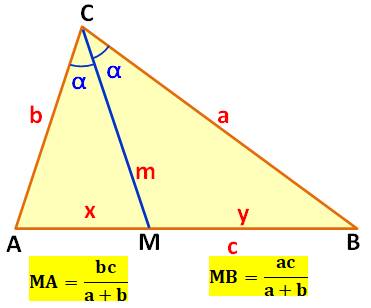
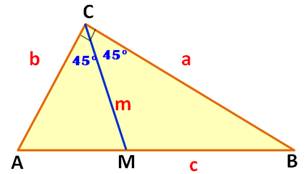
Propriété La droite CM est la bissectrice de l'angle ACB. Elle découpe le côté opposé en deux segments MA
et MB dont on donne la longueur sur cette figure. Démonstration pour x = AM
|
|
|
|
Longueur de la bissectrice Formule pour d; à adapter pour les deux autres.
Voir Démonstration |
|
|
|
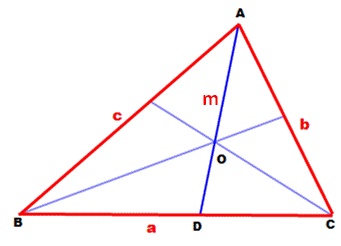
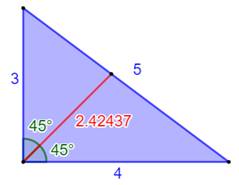
Cas de la bissectrice de l'angle
droit
Explications
Exemple
(Figure du bas)
|
|
|
|
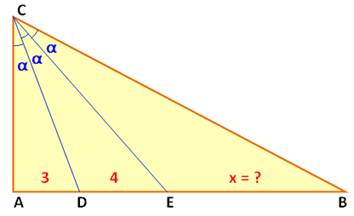
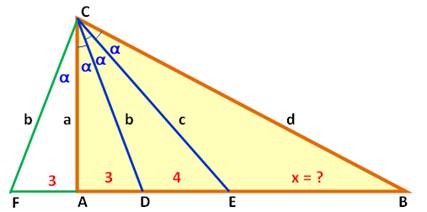
Trisection de l'angle Le triangle ABC est rectangle. L'angle ACB est partagé en trois angles égaux. Ceux-ci découpent le côté Ab en trois segments. Dans ce cas particulier, AD = 3 cm; DE = 4 cm;
et, on cherche à déterminer la longueur x de EB. Piste C'est le théorème de la bissectrice qui entre
naturellement en action. On a, par exemple: CA / 3 = CE / 4. Calculs
|
Figure initiale
Figure de travail L'idée qui va simplifier le raisonnement consiste
à construire le triangle symétrique du triangle CAD.
|
|
Pour aller plus
loin …
|
Calcul des longueurs a, b, c et d Théorème de la bissectrice et théorème
de Pythagore
|
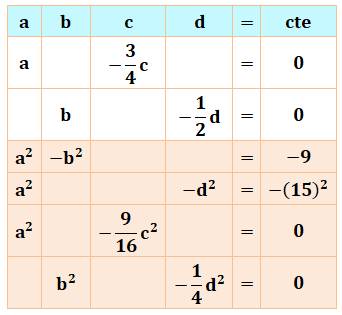
Note sur la méthode Pour la résolution du système
d'équations, on adopte une présentation en tableau qui facilite
grandement la vision des opérations à mener. Illustration avec GeoGebra
|
|
|
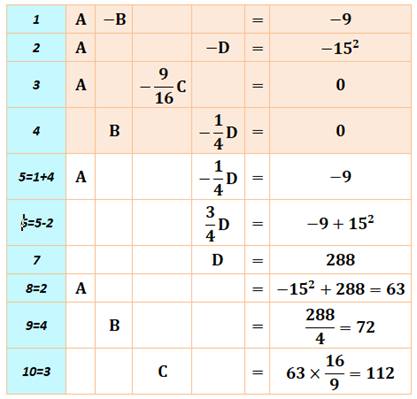
Changement de variables: A = a², B
= b², C = C² et D = d²
|
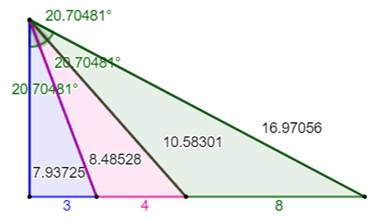
Retour aux longueurs et calcul de
l'angle
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |