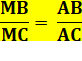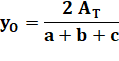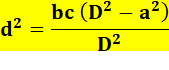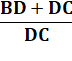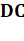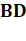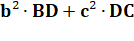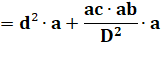|
||||||||
DicoMot: Bissectrice
/ Anglais:
angle bisector
|
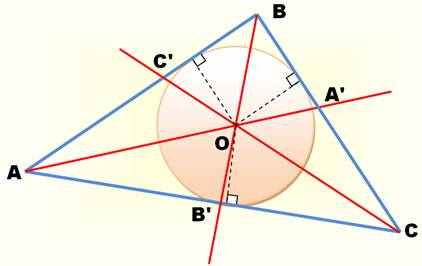
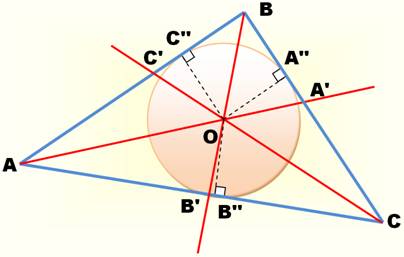
Triangle ABC. Bissectrices internes qui se coupent en O
(vertes); centre du centre inscrit. Bissectrices externes qui se coupent en Oa, Ob et
OC (pointillés roses); centres des trois cercles exinscrits. Les points de tangence M, N et P (pieds des
perpendiculaires issues des points en O) forment le triangle de Gergonne. Les droites AN, BM et CP se coupent en un seul
point, le point
de Gergonne. |
|
|
|
|
|
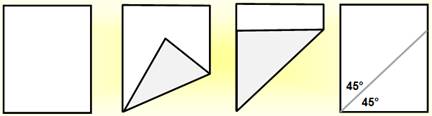
Prenez une feuille de papier;
amenez le bord-bas vers le bord-gauche et pliez. La marque de la pliure est la bissectrice de l'angle droit bas gauche;
on a divisé l'angle droit en deux parties égales (45°).
|
||
|
Définition |
Bissectrice d'un
angle: demi-droite issue du sommet de l'angle et qui le partage en
deux parties égales;
notez qu'il en existe deux pour
chaque angle: la bissectrice interne et la bissectrice externe; les trois
bissectrices internes d'un triangle se coupent en un même point, centre du cercle
inscrit dans le triangle. |
|
|
Formalisation |
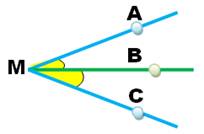
La demi-droite
[MB) est la bissectrice de l'angle |
|
|
PH = PK P'H' = P'K' |
|
|
|
Propriété induite |
Les triangles MPH et MPK d'une part et MPH' et MPK' d'autre part sont
isométriques; donc les triangles HPH' et KPK' le sont également. |
|
![]()
|
Avec un compas de centre O dessinez M et M'; Puis avec la même ouverture de compas dessinez un
arc de cercle de centre M et un autre de centre M'; Ils se croisent en B; OB est la bissectrice de l'angle
MOM'.
|
|
|
Terminologie |
On dit: Bissectrice de l'angle ou bissectrice du secteur
angulaire. La bissectrice telle que représentée ci-dessus
est la bissectrice intérieure de l'angle; en prolongeant OB
au-delà de O, on forme la bissectrice extérieure de l'angle. |
|
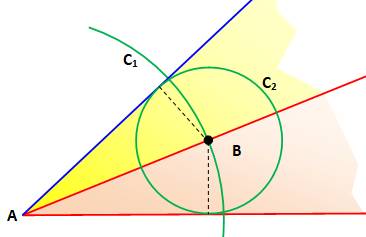
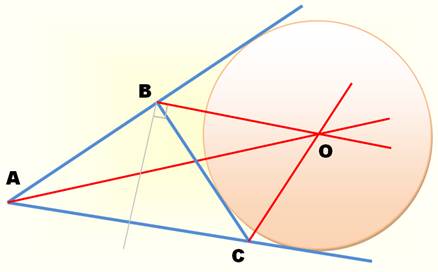
Doubler un angle |
Pour dupliquer l'angle rouge: 1.
Cercle de centre A et de rayon quelconque. Intersection en B. 2.
Cercle C1 de centre B et tangent à l'autre côté de l'angle. 3.
Tangente au cercle C2, issue de A. L'angle en jaune est
égal à l'angle en rose.
|
![]()
|
|
Voir Démonstration / Points du
triangle Le cercle inscrit dans le triangle est tangent
aux trois côtés du triangle.
Note: bissectrice intérieure et bissectrice extérieure sur un même sommet
sont perpendiculaires (bissectrices de deux angles dont la somme est un plat
– 180°).
Voir Triangle et cercle
/ Cercles exinscrits –
Développements |
|
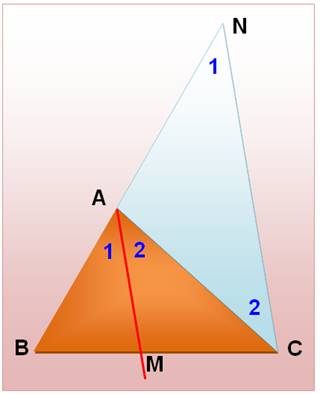
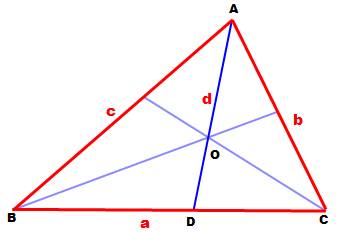
Théorème
de la bissectrice |
Dans le
triangle quelconque, la bissectrice AM découpe une sécante BC dans le rapport
des côtés adjacents AB et AC.
Voir Démonstration |
|
A circle which touches one side of a
triangle and the other two produced is
called an escribed circle of the triangle. Un
cercle exinscrit à un triangle tangent à
un côté et aux deux autres prolongés. |
Voir Faux-amis anglais
|
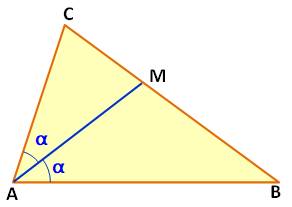
Hypothèses Un triangle ABC; AA' et CC' deux bissectrices qui se coupent en O. Ce qu'il faut démontrer La droite BB' est la troisième bissectrice. Démonstration Le point O étant sur la bissectrice AO de l'angle BAC, il est à égale
distance des côtés: OB" = OC". Le point O étant sur la bissectrice CO de l'angle ACB, il est à égale
distance des côtés: OB" = OA". D'où l'égalité: OB" = OC" = OA" Autrement-dit, le point O est à égale distance des côtés AB et AC de
l'angle ABC. Il est situé sur la bissectrice de cet angle; BB' est la troisième
bissectrice. |
![]()
|
Théorème de la bissectrice |
|
|
Démonstration |
La démonstration est d'une grande simplicité à condition d'une petite
astuce de tracé.
|
Voir Application au partage d'un
triangle en sept parties de même aire /
Défi des trois angles égaux
/ Construction du
pentagone / Brève
55-1091
![]()
|
Antiparallèles |
Droites D et D'
et droites d et d'. Les bissectrices des angles (pointillés). Si la
direction de ces deux bissectrices est la même, alors d' (par exemple) est l'antiparallèle de d par rapport à DD'.
Si A et B sont confondus, alors les couples de
droites sont dites isogonaux. Voir Points cocycliques |
|
Ligne isogonale |
Soit un angle et sa bissectrice; une ligne symétrique
par rapport à la bissectrice est son isogonale.
|
|
Propriétés |
Dans un triangle, si trois droites
issues des sommets sont concourantes, alors leurs isogonales sont
concourantes. Voir Symédiane
|
![]()
|
Anglais |
Note de prudence: souvent ce mot est pris pour
diviser en deux, pas forcément en parts égales. Prononciation: [ˌbaɪˈsekt] en gros: baille secte. Orthographe (un "s" ou
deux; parts égales ou non?)
The internal bisector and external
bisector of an angle.
The three angle bisectors of a triangle intersect in
a single point; this point is the center of the triangle's incircle,
the circle which lies inside the triangle and touches all three sides. There are
three other important circles, the excircles; they lie outside the triangle
and touch one side as well as the extensions of the other two. |
![]()
![]()
Section
avancée*
|
|
||
|
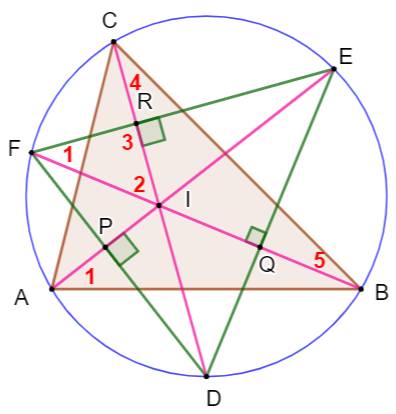
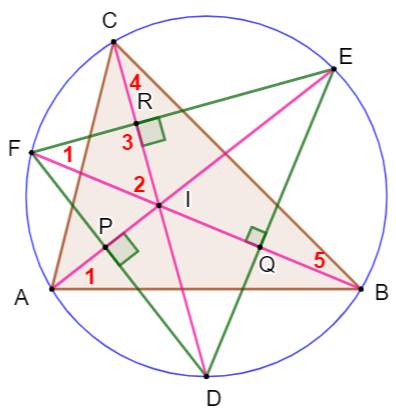
Construction Triangle ABC et son cercle circonscrit. Bissectrices (roses). Intersections avec le cercle en D, E et F Propriété Les côtés du triangle DEF (vert) sont
perpendiculaires avec les bissectrices. Démonstration On note A, B et C les angles en ces sommets. Même arc intercepté: angles 1 égaux, et ils
valent A/2. Angle 2 = 180 – BIC = 180 – (180 – 4 – 5) = 4 +
5 = B/2 + C/2 Triangle: 1 + 2 + 3 = 180 = A/2 + B/2 + C/2 +
3 = 180/2 + 3 |
|
|
Voir Triangles
remarquables / Brève
863
|
|
||
|
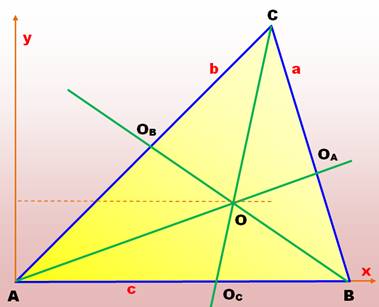
Quelles sont les coordonnées
du point O?
Avec AT l'aire du
triangle ABC (voir formules de Héron). Même formules avec
permutations pour les autres bissectrices. |
|
|
Voir Rayon du cercle inscrit
/ Calculs pour l'orthocentre / Droite d'Euler
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
![]()
|
En savoir plus |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosB/Bissectr.htm |
![]()