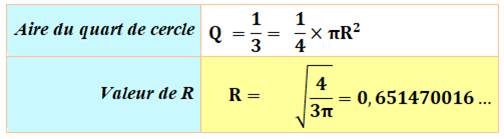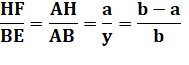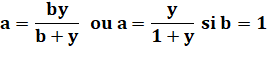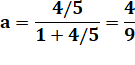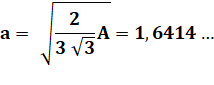|
Édition du: 15/07/2023 |
|
INDEX
|
CARRÉ |
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
Carré – Partage Comment partager le carré
en k polygones
de même aire
? Solutions pour 3, 5, et 7 formes géométriques. Il existe une solution simple avec des rectangles,
il suffit de découper le carré en k bandes. Oui mais, comment construire ces bandes rectangulaires ? |
||
|
|
Sommaire de cette page >>> Partages simples du carré >>> Le carré divisé en trois bandes >>> Le carré divisé en trois quadrilatères >>> Le carré en trois quadrilatères (bis) >>> Le carré en trois avec arcs de cercle >>> Le carré avec arcs de cercle (bis) >>> Le carré divisé en bandes (sept et neuf) >>> Le carré divisé en sept polygones >>> Le carré divisé en cinq polygones |
Débutants Glossaire |
|
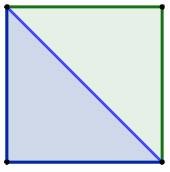
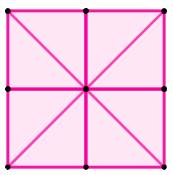
Partage en 2 et en 8
|
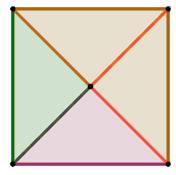
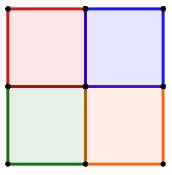
Partage en 4 (deux possibilités)
|
|
|
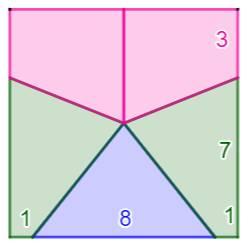
Partage en 5 – Carré 10 x 10 avec cinq polygones d'aire 20.
|
||
|
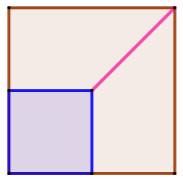
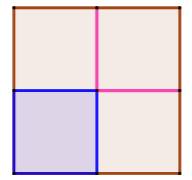
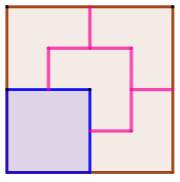
Partage du carré évidé d'un carré (en bleu) en
deux, trois et quatre polygones superposables
|
||
|
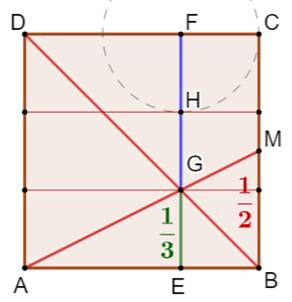
Partage du carré en trois bandes Comment créer trois bandes à la règle et au compas ou même par
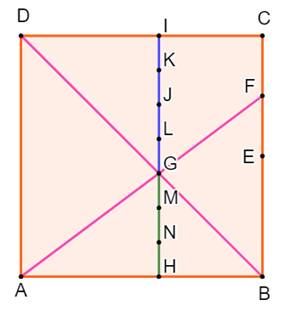
pliages. Construction Carré ABCD. Diagonale BD. Point M milieu de BC. Segment AM; intersection G. Parallèle en G à BC. Notez que EB = EG (triangle isocèle). Alors GE = 1/3 du côté du carré (Voir démo). Report de la distance GE en FH. Dessin des trois bandes passant par G et H. |
|
|
Voir Brève
49-961
|
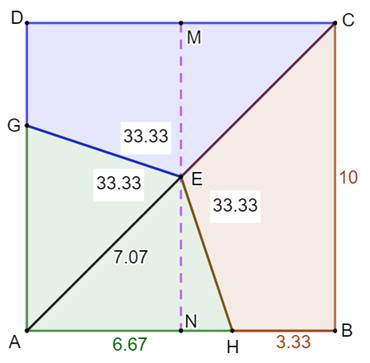
Partage du carré en trois Soit un carré de 10 cm de côté. Comment le partager en trois
quadrilatères non-rectangulaires de même aire; Construction Diagonale AC du carré. Médiatrice MN. Tiers sur les côtés: DG et BH. (Avec application de la construction vue ci-dessus). Les quadrilatères colorés ont la même aire. Ils ne sont pas
superposables. |
|
||
|
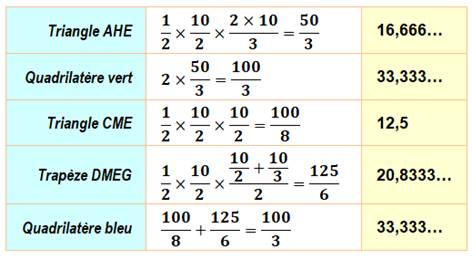
Vérification Calcul de l'aire de chacun des deux types de
quadrilatères par morceaux: triangles et trapèze. |
Aires
|
||
Voir Brève
48-950
|
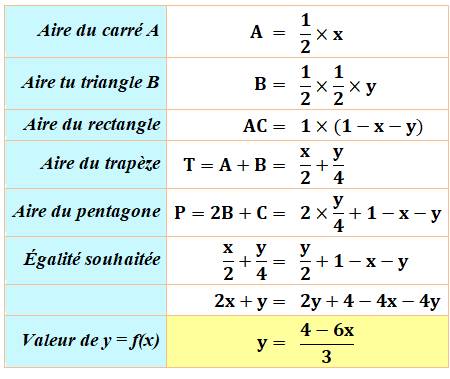
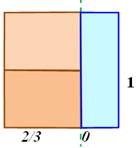
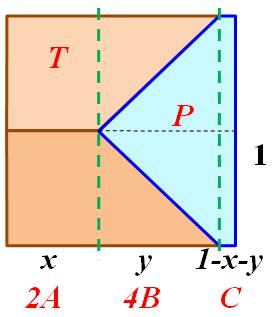
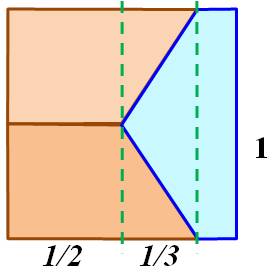
Partage du carré en trois Soit un carré de 1 cm de côté. Comment le partager en trois
quadrilatères non-rectangulaires de même aire; Solution La figure montre un type de solution. L'aire de chaque forme colorée (trapèze
et pentagone) est égale à 1/3. Calcul de x et y
Cas extrême avec x = 2/3
|
Solution et notations
Exemple avec x = 1/2
|
|
|
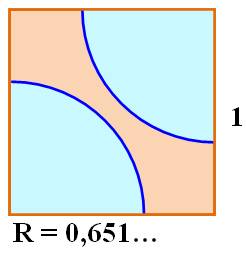
Partage du carré en trois avec arcs de cercle Comment deux arcs de cercles peuvent partager le carré en trois
surfaces de même aire ? Solution L'aire du quart de cercle doit être égale à 1/3.
|
Solution
|
|
|
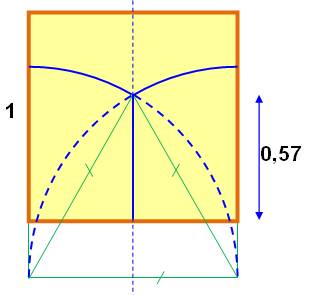
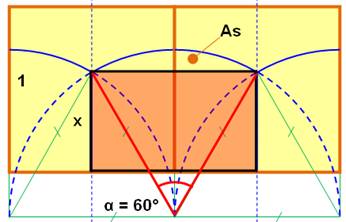
Partage du carré en trois avec deux arcs de
cercle Partager le carré en trois formes de même aire avec deux arcs de
cercle et un segment médian. Construction Pour un carré de côté unité, le segment médian mesure: 0,57608059 … À partir de la pointe de ce segment, tracer un triangle équilatéral de
côté unité dont un côté est parallèle à un coté du carré. Cercles de rayon unité à partir des deux autres sommets du triangle
équilatéral. Calculs de x On note x la longueur du segment médian. La figure est dupliquée. La surface considérée sera égale à 2 fois 1/3
du carré. Il s'agit du rectangle ocre surmonté d'un segment
de cercle dont l'aire est As. |
Solution
|
||
|
|
|
||
|
Construction pour SEPT bandes Plus grande puissance de 2 inférieure à 7 : 4 Milieu de BC, puis milieu de CE: point F. Parallèle à BC en G. Milieu J de GI, puis milieux de IJ et de JG. Le segment IH est divisé en sept. Généralisation Cette méthode est applicable à tout nombre autre que k = 7. La
construction pour k = 3 est celle montrée ci-dessus. Et,
pour k = 9, ci-dessous. |
Illustration
Cette figure est constructible à la règle
et au compas ou même par simple pliage. |
|
|
Construction pour NEUF bandes Plus grande puissance de 2 inférieure à 9 : 8 Milieu trois fois sur le côté pour obtenir 1/8 du côté. Deux droites roses. L'intersection est au (9 – 8) / 9 =
1/9 du côté. Il suffit de reporter cette longueur sur le segment vertical. Les mesures sont données pour un carré 10x10. |
|
|
|
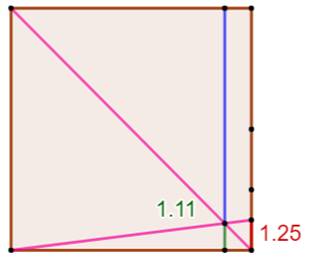
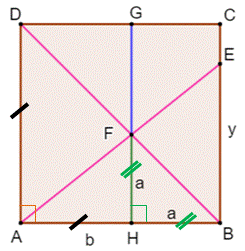
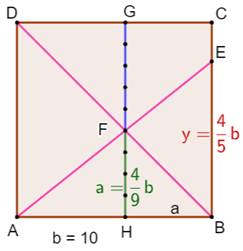
Le triangle HBF est isocèle
rectangle de côté a, car le point F est sur la diagonale du carré. En effet: par construction, les angles DAB et FHB
sont droits. L'angle DBA est commun. Avec deux angles identiques, ces deux triangles
sont semblables
et leurs côtés proportionnels. Via les triangles semblables ABE et AHF: |
|
|
|
Exemple Avec EB = 4/5 La valeur de a est alors: Soit la construction ci-contre. En pratique On choisit une puissance de 2 pour y, de manière à obtenir une
fraction constructible à la règle et au compas et même par simple pliage. |
|
|
Voir Construction des
fractions / Construction
des fractions quelconques
|
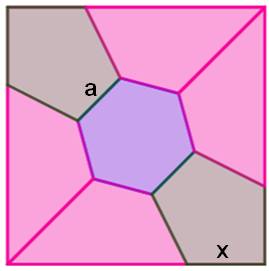
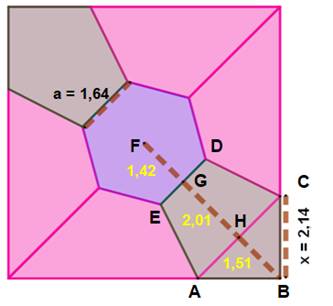
But Découper le carré en SEPT formes de
même aire. On exclut la solution du découpage en sept bandes rectangulaires. L'idée consiste à proposer un hexagone central. Construction Cette construction est impossible à la règle et
au compas; il faut calculer et reporter des longueurs. Dans le carré de 7 cm de côté: un hexagone central de 1,64 cm de côté
(a) avec une rotation de 45 °. Deux sommets de l'hexagone rejoignent deux sommets du carré (diagonale
du carré). Sur les autres sommets du carré, on reporte la longueur x = 2,14, ce
qui permet de dessiner les deux pentagones verts. Chacune de ces formes à une aire égale à 7 cm². |
Illustration
Figure construite avec Geogebra |
|
|
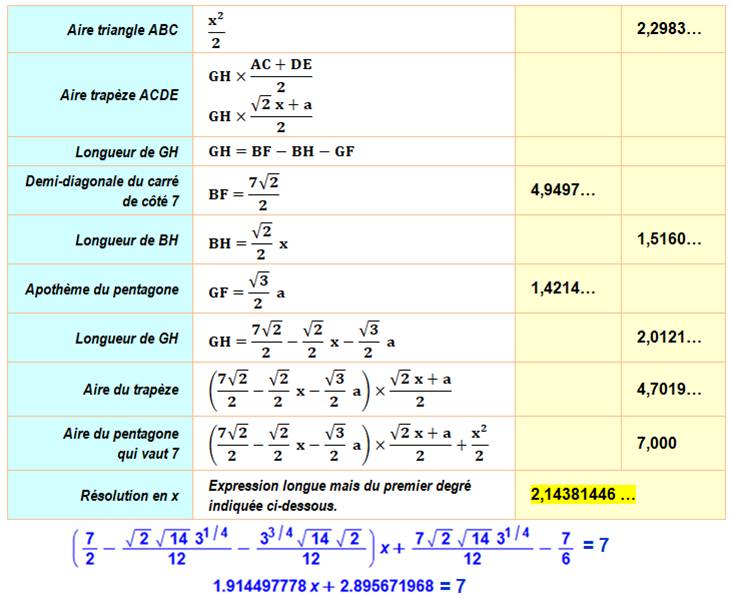
Calcul de a L'hexagone
est construit pour une aire A = 7². |
Notations
|
|
|
Calcul de x Colonnes jaunes: à gauche, valeurs numériques calculable et, à droite,
valeurs en supposant x connu.
|
||
Sur une
idée de KevinFinity
Voir Brève
49-960
|
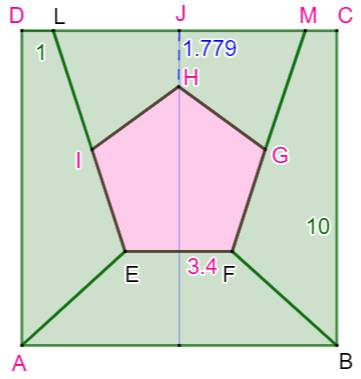
Construction pour CINQ polygones non rectangulaires avec pentagone
central La construction précédente peut être généralisée à loisir dans la
mesure où elles sont réalisées en connaissant les longueurs à reporter. Les longueurs indiquées sur cette figure doivent suffire à la
construction. Cette figure, servant à
connaitre les longueurs, a été
construite avec Geogebra en
ajustant les aires à 20 pour chacun des cinq polygones totalisant une aire de
100. |
Illustration – Voir pentagone
|
|
Haut de page (ou double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |