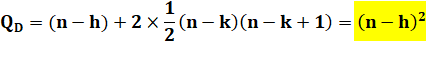Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 10/03/2024 M'écrire Brèves de Maths

INDEX Polygones Carrés Géométrie Dénombrement Jeux et énigmes	QUADRILATÈRES – Compter
	Quadrilatère	Triangles dans rectangle	Grille & segments unitaires
	Carré	Triangle dans le carré	Grille & tous segments
	Rectangle	Carrés et cercles	Grille & triangles rectangles
	Trapèze	Carré (un) dans le carré	Grille & triangles équilatéraux
	Parallélogramme	Carrés dans le carré	Grille & carrés
	Losange	Carrés dans rectangle
	Polygones	Rectangles dans carré	Rectangles – Énigmes
		Rectangle dans rectangle	Pièce de puzzle
		Quadrilatère dans le carré

Quantité de segments entre k points dans une grille n × n Sur une grille, on compte tous les segments droits qui relient k points: les traits horizontaux, verticaux, en diagonales à 45°, mais aussi toutes les autres droites obliques. Le dénombrement n'est pas facile et, en général on s'en remet à un algorithme traité par logiciel. Le cas de segments reliant 8 points est traité.
	Sommaire de cette page >>> Approche avec grille 3x3 >>> Grille 4x4 & 3-segments >>> Grille 5x5 & 3-segments >>> Grille nxn & 8-segments	Débutants Géométrie Glossaire Géométrie

Approche avec grille 3x3		haut
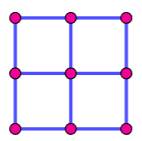
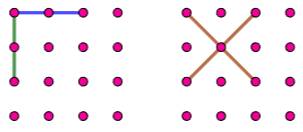
La grille est définie par sa quantité de points et non sa longueur. La grille 3×3 comporte 3×3 = 9 points. Combien de segments entre deux points ? Sur une grille 3x3, il existe 6 segments entre deux points horizontaux et 6 autres entre deux points verticaux. Il existe également 8 (4 + 4) segments entre deux points en diagonales. Nous disons bien entre deux points, sans se soucier de la longueur du segment. 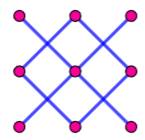Notation Par souci de simplification d'écriture, on note: k-segment pour un segment droit compris entre k points. Combien de 3-segments (Figure du bas) ? 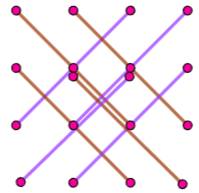Comptons les 3-segments reliant trois points: Horizontaux: 3 Verticaux:3 Diagonales: 1 + 1 Total: 8 cas de 3-segments sur grille 3x3	Segments sur grille 2x2 20 2-segments entre deux points 8 3-segments entre deux points

Grille 4x4 & 3-segments		haut
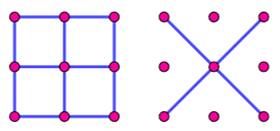
Grille 4x4: combien de 3-segments ? Sur cette grille 4x4, on compte les segments entre trois points: Bleu: 2 par ligne et 4 lignes: 8 Vert: 2 par colonne et 4 colonnes: 8 Marron: 2 fois 4 diagonales: 8 Total: 3 × 8 = 24 cas de 3-segments sur grille 4x4 Calcul avec n, la quantité de points par côté Avec cette approche, on peut formaliser: Bleu: (n – 2) par ligne et n lignes: n(n – 2) Vert: (n – 2) par colonne et n colonnes: n(n – 2) Marron: (n – 2) par diagonales et 2 fois (n – 2) diagonales: 2 (n – 2)² Voir décompte des diagonales ci-dessous Total: Q3 = 2n(n – 2) + 2 (n – 2)² = 4n² – 12n + 8 Et pour des segments entre k points et h intervalles: Q = 2n(n – h) + 2(n – h)² Après simplification: Q = 4n² – 6nh + 2h²	Trois types de segments Les segments droits relient k = 3 points et couvrent h = 2 intervalles. Toutes les 3-diagonales

Compter les diagonales

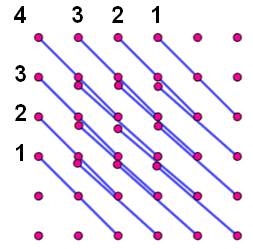
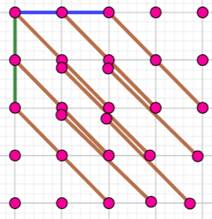
Comptons les 3-segments sur les diagonales descendantes de cette grille 6x6. On a: n = 6, k = 3 (points) et h = k – 1 = 2 (intervalles). Diagonale centrale: 4 segments ou n – h Diagonales du haut: 3 + 2 + 1 segments ou ½ (n – k)(n – k + 1) qui est la somme des entiers, ici de 1 à 3. Total

Grille 5x5 & 3-segments		haut
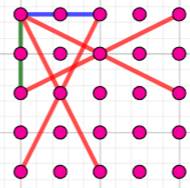
Grille 5x5 Application de notre formule pour k = 3, donc h = 2: Q = 4 × 5² – 6 × 5 × 2 + 2 × 2² = 48 Vérification Bleu: 3 par ligne et 5 lignes: 15 Vert: 3 par colonne et 5 colonnes: 15 Marron: (n – h)² = (5 – 2)² = 9 Total: 15 + 15 + 2 × 9 = 48 segments; conforme ! Diagonales supplémentaires (Figure du bas) Sur cette grille, d'autres "diagonales" apparaissent en plus des diagonales classiques à 45°. On en compte 3 de quatre types: 12. Soit un nouveau total: 48 + 12 = 60 segments de longueur 2. Formulation Pas évident de trouver une formule générale pour compter ces segments en diagonales. À l'heure des ordinateurs, on préfère un algorithme implanté en logiciel.	Diagonales à 45° Autres diagonales; à droite: les 12

Grille nxn & 8-segments		haut
Dénombrement Ce cas est identifié par l'encyclopédie en ligne des suites d'entiers: OEIS A177724 - Number of line segments connecting exactly 8 points in an n x n grid of points. On y trouve aussi l'algorithme de calcul sous logiciel Mathematica Cas des grilles 8 à 14 Pour 8x8, le compte est facile à établir: 8 + 8 + 2 = 18. Ce qui conforme à la formule comptant les segments horizontaux, verticaux et obliques à 45°. Cela est valable jusqu'à la grille 14x14. Cas de la grille au-delà de 14 Pour 15x15, la formule donne 368 segments, et il y a 32 nouvelles obliques pour 40 segments au total. La courbe de croissance de ces quantités de segments est exponentielle, proche du troisième degré. 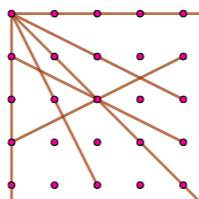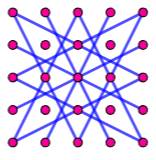Quelque chose comme: Q = 0,417x^3 – 10,278x² + 108,683 x + 431	Grille 22x22 – 1372 possibilités de 8-segments En bleu, quelques exemples. Il y a 262 obliques non à 45°. Quantité de segments [n, Q] n x n est la quantité de points sur la grille. Q est la quantité de segments entre huit points. Avec diagonales à 45° [8, 18], [9, 44], [10, 78], [11, 120], [ 12, 170], [ 13, 228], [ 14, 294], Avec autres obliques [ 15, 400], [ 16, 522], [ 17, 660], [ 18, 814], [ 19, 984], [ 20, 1170], [ 21, 1372], [ 22, 1682], [ 23, 2024], [24, 2398], [ 25, 2804], [ 26, 3242], [ 27, 3712], [ …

Suite	Quantité de droites passant par n points sur une grille Quantité de carrés dans le quadrillage d'un rectangle Constructions élémentaires: rectangle Le terrain de basket Losange Pavage avec des rectangles Quadrilatères – Juniors
Voir	Allumettes en carrés Allumettes et quadrillage Carré Construction à la règle et au compas Dénombrer – Index DicoMot Maths Énigmes classiques Ensembles – les compter Géométrie Pentominos Jeux – Index
Sites
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/Seg8Gril.htm