|
Édition du: 03/07/2021 |
|
INDEX |
Apollonius – Constructions |
||||
|
PPP (1) |
PLL 4) |
LLL
(3) |
CCC (10) |
||
|
PPL (2) |
PLC (6) |
LLC (5) |
|||
|
PPC (8) |
PCC (9) |
LCC (7) |
|||
![]()
|
Construction d'Apollonius Deux points et un cercle (PPC) Comment
construire un cercle tangent à un cercle et passant par deux points ? Cette page propose une approche générale. On
ne traite pas des cas particuliers conduisant à des d'impossibilités. |
||
|
|
Sommaire de cette page >>>
Deux cercles et un point >>>
Méthode par inversion |
Débutants Glossaire |
|
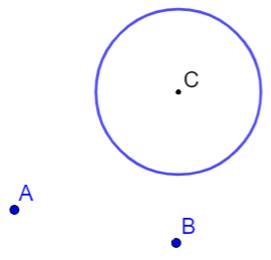
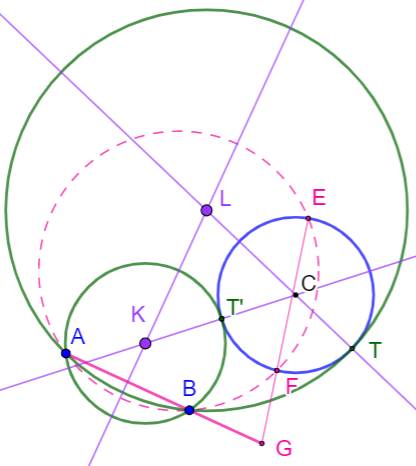
But Construire le cercle tangent au cercle C et
passant par les deux points A et B. |
|
|
|
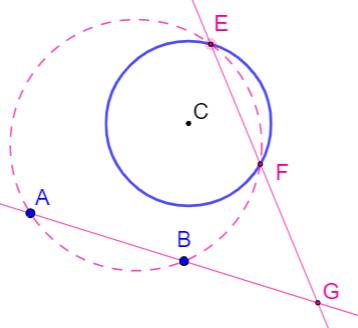
Construction Un cercle quelconque qui passe par A et B et qui
coupe le cercle de consigne (C) en deux points E et F. Intersection G des droites AB et EF. |
|
|
|
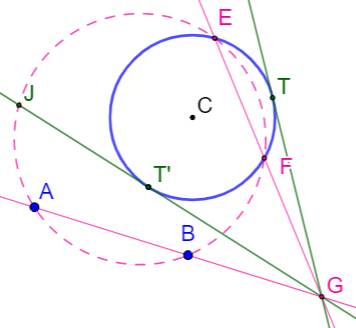
Tangentes au cercle à partir de G. Points de tangence T et T'. |
|
|
|
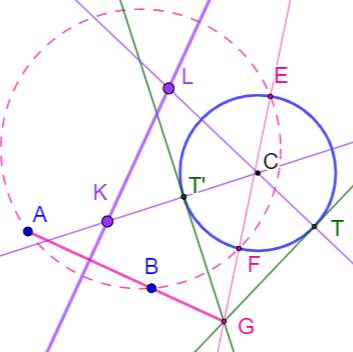
Figure légèrement modifiée pour meilleure
lisibilité Médiatrice de AB (violet). Droites CT et CT' Intersections K et L avec la médiatrice. Ce sont les centres de cercles cherchés. |
|
|
|
Cercles (verts) de centre K et L et passant par A
et B. Ils sont tangents au cercle initial. Propriété: Le point G est le point
radical des trois cercles |
|
|
Voir
Construction par méthode de l'inversion >>>
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |