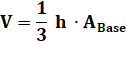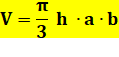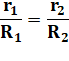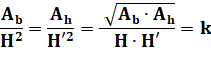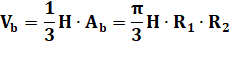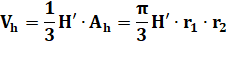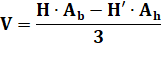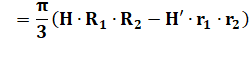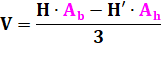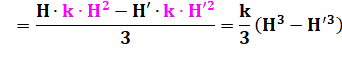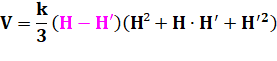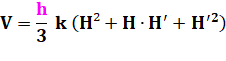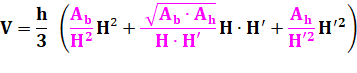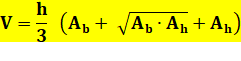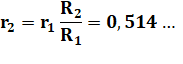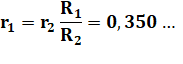|
||||||||||||||||||||||||||||||||||||||||
![]()
|
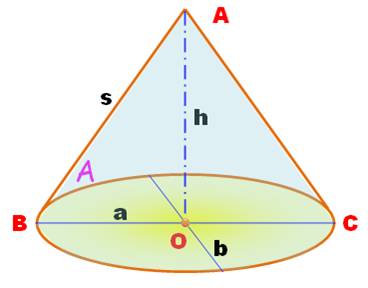
Cône et tronc de cône ELLIPTIQUE Il s'agit
ici de cône dont la surface de base est une ellipse.
Le cône peut être quelconque ou droit (le sommet est situé sur la perpendiculaire
levée au centre de l'ellipse). On
connait simplement le volume du tronc d'ellipse classique. Par contre, le cas
du volume compris entre deux ellipses quelconques est plus difficile à
résoudre. |
Voir Exemple
pratique du tas de terre
|
|
||
|
Comme toutes les pyramides, le volume est égal au tiers
du produit de la hauteur par l'aire de la base. L'aire de l'ellipse est connue
en fonction des deux demi-axes a et b.
|
|
|
Tronc d'ellipse ou volume entre ellipses
|
Dans le cas du "tronc"
d'ellipse deux cas se présentent:
|
|
|
|||
|
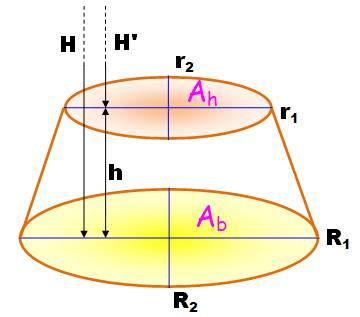
Le tronc
de cône résulte de la suppression d'un petit cône chapeau à partir d'un grand
cône. Les deux ellipses sont dans des plans parallèles. Alors les
longueurs des axes sont proportionnelles:
Également,
relation de proportionnalité avec les aires et le carré des altitudes des
ellipses:
|
|
||
|
Volume du
grand cône elliptique: |
|
||
|
Volume du
petit cône elliptique: |
|
||
|
Volume du
tronc de cône elliptique: |
|
||
|
En
reprenant l'expression des aires en fonction de k : |
|
||
|
En
factorisant : |
|
||
|
Hauteur
du tronc de cône: |
|
||
|
En
remplaçant k par ses valeurs respectives: Voir Moyenne
héronienne |
|
||
|
Volume entre elliptiques
parallèles |
|
|
|
La
formule en moyenne héronienne n'est pas valable pour deux surfaces non similaires
(qui ne résultent pas de la section par deux parallèles d'un même solide (pyramide ou cône). |
Un calcul par
intégrales avec mise en équation des deux surfaces est nécessaire. |
|
|
Cas concret (avec approximations) Dans le
cas de deux ellipses parallèles, comment approximer le volume ? Exemple
de calcul de la capacité d'un bidon qui correspond à un quart de cette forme
elliptique. |
Données (en m) R1 = 0,7; R2 = 0,6 r1 = 0,6; r2 = 0,35 h = 1,9 |
|
|
Les
proportions sont vraiment différentes (non proportionnelles). |
r1 / R1 = 0,857… r2 / R2 = 0,583… |
|
|
Calcul 1 Comme
s'il s'agissait d'un tronc de cône. |
Ab = 1,319… Ah = 0,659… V = 1,844… m3 |
|
|
Calcul 2 On
conserve trois valeurs et on déduit la quatrième r2 redéfinit. |
Ab = 1,319… Ah = 0,969… V = 2,165… m3 |
|
|
Calcul 2 bis Idem avec
r1. |
Ab = 1,319… Ah = 0,385… V = 1,530… m3 |
|
|
Moyenne de ces deux calculs |
V = (2,165 + 1,530) / 2 V = 1,847… m3 |
|
|
Calcul 3 Proportion
moyenne et petits axes recalculés. |
k = (0,857 + 0,35)/2 = 0,720…
Ab = 1,108… Ah = 0,814… |
|
|
Bilan Ces trois
calculs sont assez concordants sans garantie de justesse ! |
V Vbidon |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()