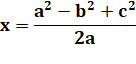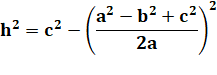|
Édition du: 25/01/2021 |
|
INDEX |
CONSTRUCTION – TRIANGLE |
||||
|
Constructions |
LAL
… |
||||
|
MMM |
|||||
L:
côté; A: Angle; h: hauteur; m: médiane; M: médiatrice; b: bissectrice
![]()
|
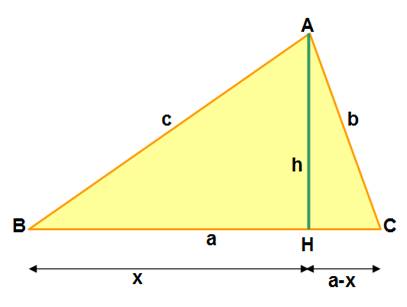
Résolution des triangles Participation de la hauteur La résolution d'un triangle consiste à trouver
les trois mesures manquantes lorsqu'on en connait trois. La loi des sinus
et la loi des cosinus sont commodes pour
venir à bout de ce type de problème. Sans les connaitre, il est possible de dessiner
une ou plusieurs hauteurs et de procéder aux calculs de simple trigonométrie.
Si la longueur d'une ou de plusieurs hauteurs
sont connues, comment s'y prendre? |
||
|
|
Sommaire de cette page >>> Figure
& notations >>> Calcul de
l'aire – Exemple >>>
Formules >>> Construction avec la longueur des trois
hauteurs |
Débutants Glossaire |
Anglais: Triangle (location)
construction problems
|
|
||||||||||||||
|
|
|||||||||||||
|
|
||||||||||||||||||||||||||||
|
Calcul pour se familiariser avec a = 21; b = 17; c = 10 unités de
mesure.
|
||||||||||||||||||||||||||||
Voir Formules de calcul de l'aire du triangle quelconque
|
|
||
|
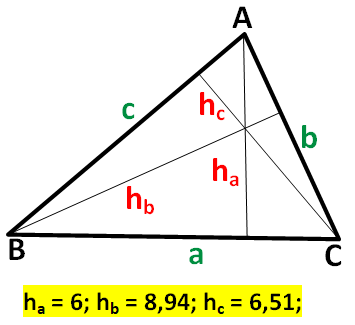
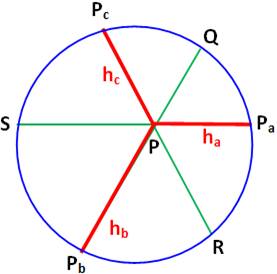
Données ha,
hb et hc les longueurs des hauteurs Exemple Les
seules données sont celles indiquées en jaune. Il s'agit
de restituer le triangle ABC dont les hauteurs ont les longueurs spécifiées. |
|
|
|
Construction
(1/2)
|
|
|
Voir Toutes les
constructions du triangle
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/RelQuelh.htm
|
![]()