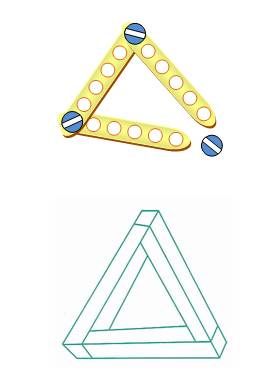|
||||||||||||||||||||||||||||
![]()
|
|
||
|
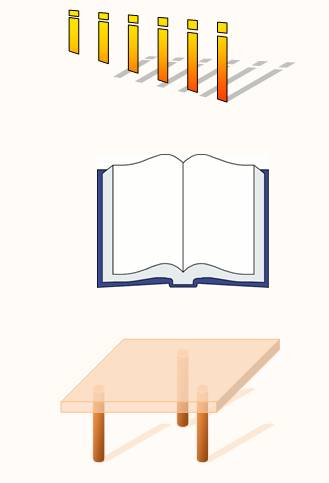
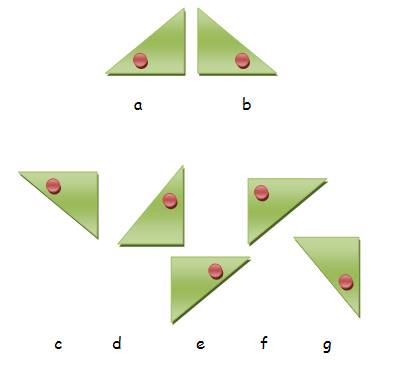
D'un point, j'en fais un axe de
rotation, comme le point autour duquel tournent les aiguilles d'une montre ou l'axe de ma manette de jeux
(joystick).
Avec une droite, je fais une charnière
comme la reliure de mon livre ou les
gonds de la fenêtre.
Sur trois points, je
peux poser une plaque de métal: elle est en équilibre et elle est bien en
contact avec les trois points; avec quatre ce serait
très difficile. C'est le principe de stabilité d'un
tabouret à trois pieds ou du chevalet du peintre ou du tableau mobile dans
les salles de réunion. |
|
|
|
|
||
|
Le triangle est simple! Oui! Mais que
d'études sur lui. Et cela depuis l'Antiquité.
La figure ci-contre montre un triangle
impossible, une illusion |
|
|
|
|
||
|
|
|
|
|
|
||
|
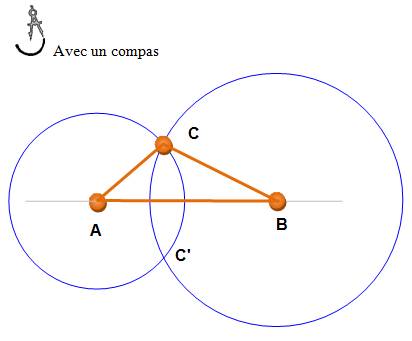
Problème
AB = 5 cm AC = 2,5 cm BC = 3,5 cm Construction 1) Je
trace le segment AB qui mesure 5 cm avec une règle graduée 2) J'ouvre
le compas à 2,5 cm et je trace le cercle de centre A 3) J'ouvre
le compas à 3,5 cm et je trace le cercle de centre B 4) Les
deux cercles se coupent en C (on peut aussi prendre l'autre point
d'intersection C', en bas, bien sûr). |
|
|
|
|
||
|
|
|
|
|
|
||
|
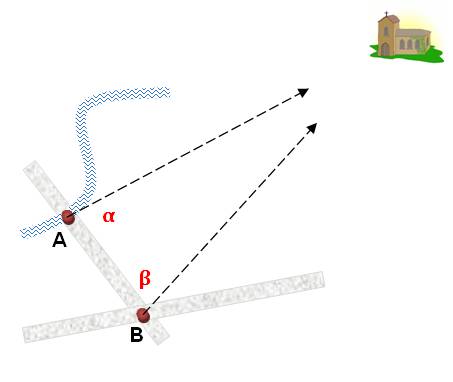
La connaissance de la distance entre A et B et des deux
angles alpha et bêta permet de situer l'église et de reporter sa position (en
fait, le dessin du triangle) sur la carte par rapport aux points A (croisement de routes) et B (passage de la
rivière sous la route). Trilatération: méthode particulière de
triangulation. Contrairement à la
triangulation, qui utilise les angles et les distances pour positionner un point,
la trilatération utilise les distances entre un minimum de deux points de
référence. Utilisation notamment par le GPS.
|
|
|
Voir Triangulation des polygones (Partage des
polygones en triangles)
|
|
||
|
|
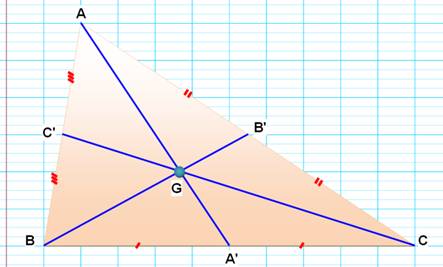
Les médianes se coupent au même point.
C'est le cas également des bissectrices, des hauteurs et des médiatrices. N'est-ce
pas spectaculaire pour un être quelconque? |
|
![]()
|
Suite |
|
|
Autres |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/TrgDebut.htm |
![]()
|
|
||
|
|
|
|