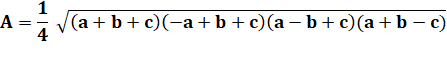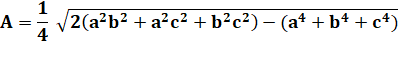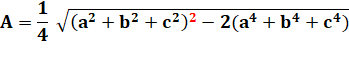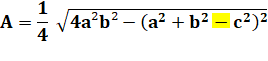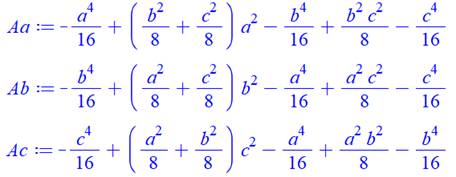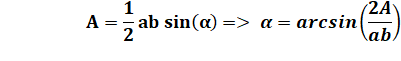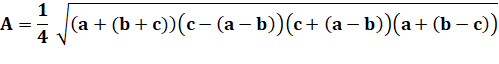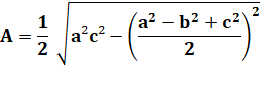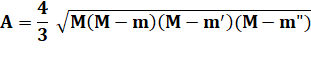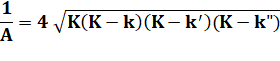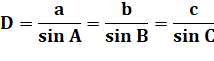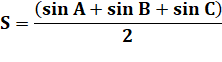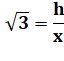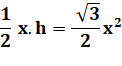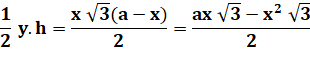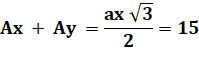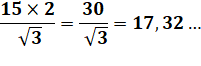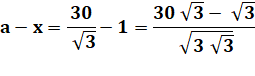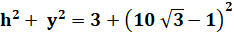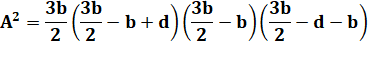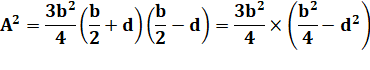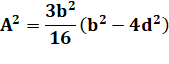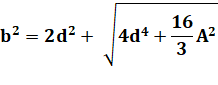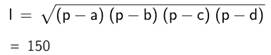|
||||||||||||||||||||||||||||||||||||||||
![]()
|
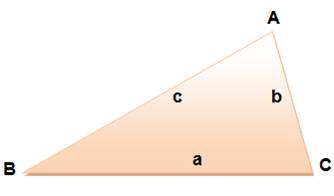
TRIANGLES QUELCONQUES Relation de Héron / Triangles héroniens La formule de Héron permet de calculer l'aire
d'un triangle quelconque en ne connaissant que les mesures des côtés. In
fine un exemple pratique de calcul dans un triangle et vérification à l'aide
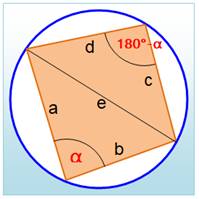
de la formule de Héron. La formule de Héron est un cas particulier pour le triangle de la formule de Brahmagupta pour un quadrilatère cyclique
(inscrit dans un cercle). |
|
Héron
d'Alexandrie (1er siècle de notre ère) calcule l'aire de
différents triangles dont le (6, 7, 8) qui donne A² = 720. Il lui faut
calculer la racine. Cette formule est sans doute antérieure, mais
Héron en donne une démonstration dans Métriques
et dans Traité de la Dioptre. Vers 600, Bramahgupta
caractérise les triangles héroniens. Au IXe siècle,
Mohammed, Ahmed et Alhasan fournissent une démonstration dans le Livre des trois frères arabes. Le
célèbre Al-Khwarizmi décrit
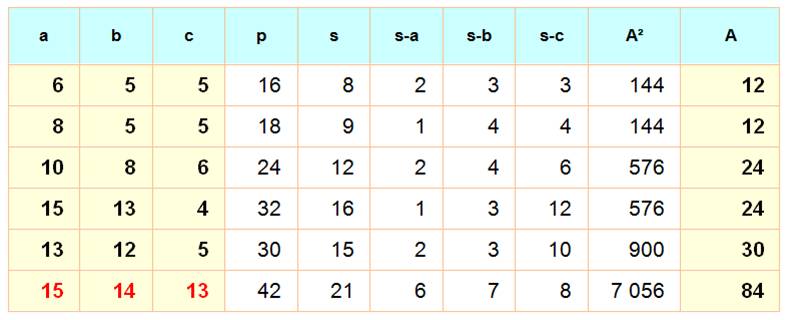
aussi cette méthode en 820. Exemple illustré par le triangle (13, 14, 15) dont la
hauteur et l'aire sont rationnelles. Fibonacci (1175-1250) reprend cette formule et sa
démonstration dans Géométrie pratique
(1220). Newton en 1707 et Euler en 1747 et d'autres chercheront
à trouver d'autres démonstrations. |
|
|
|||
|
Périmètre du tri p = s = ½ p = ½ (a + b + c) Aire du triangle
|
|
||
|
Autres manières de l'écrire Attention au carré et au signe moins signalés en couleur |
|
||
|
Formulation d'Euler |
A²
=1/16 (a + b + c)(a + b – c)(b + c – a)(c + a – b) A²
= 1/16 (2a²b² + 2a²c² + 2b²c² – a4 – b4 – c4) |
||
|
Formules en fonctions de chaque côté Aa :
Aire du triangle exprimée en fonction de a. Etc. |
|
||
|
Si on connait la longueur des côtés du triangle, on
connait son aire en utilisant la formule
de Héron. Bonus, on connait aussi les angles
par la formule
de l'aire: |
Voir Exemple d'application dans le défi des trois cercles tangents
|
Ci-dessous, avec a, b
et c par ordre croissant: |
|
|
Formule pour les calculs avec
calculette dans un
triangle avec petits angles. Mettre toutes
les parenthèses. |
|
|
Autres formules Formule
découverte par les Chinois, publiée en 1247. |
|
|
Formule avec: - les médianes (m, m'
et m") et leur demi-somme (M); -
l'inverse des hauteurs (k = 1/h, k' et
k") et la demi-somme de ces inverses (K). |
|
|
Formule avec les médianes |
|
|
Formule avec les hauteurs Attention, inverse des hauteurs |
|
|
Formules avec les angles D
est le diamètre du cercle circonscrit |
|
|
|
|||
|
Un triangle héronien
est un triangle quelconque dont les longueurs et l'aire sont des nombres rationnels. Exemples
Formules paramétriques
Triangles Périmètres égal Aire (equable triangles) Seuls cinq triangles héroniens ont
une aire égale au périmètre: (5,12,13),
(6,8,10), (6,25,29), (7,15,20) et
(9,10,17). |
|||
Voir Triangles
héroniens / Le triangle (13, 14, 15) et le triangle (5,
5, 6) / Triangle entier (17,
24, 25, 26) /
|
|
||
|
Cette
démonstration, sans doute la plus simple, est un exemple typique de l'emploi
du théorème de Pythagore
et des identités remarquables.
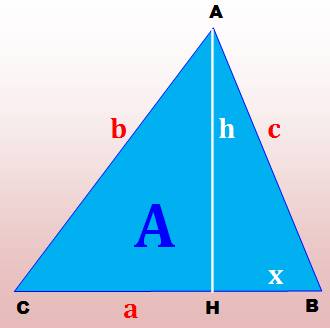
La hauteur h partage le triangle quelconque en
deux triangles rectangles. Soit deux expressions du carré de la hauteur en
fonction de la longueur des côtés. Le reste est une simple question de
calculs algébriques. |
|
|
|
|
||
Voir Aire du
quadrilatère inscrit – relation de Brahmagupta
![]()
Application à la vérification d'un calcul
|
|
||
|
Trouvez les
mesures des trois côtés: a, b et c. Remarque liminaire
|
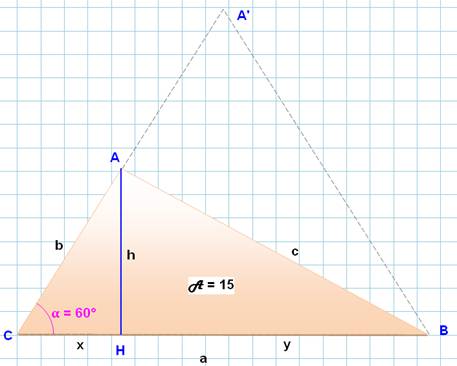
Le triangle A'BC est
équilatéral. L'angle en C est égal
à 180/3 = 60°. La hauteur h du
triangle ACH mesure x Cette valeur est
déduite de la valeur de la tangente de l'angle 60°. |
|
|
|
|||
|
Angle de 60° |
tan 60° = |
|
|
|
Hauteur du
triangle |
h = |
|
|
|
Aire du
triangle Ax |
Ax = |
|
|
|
Aire du
triangle Ay |
Ay = |
|
|
|
Aire du triangle
complet A |
A = |
|
|
|
Valeur de a si x = 1 |
a = |
|
|
|
Hauteur |
h = h² = |
3 |
|
|
Valeur de y (On sait
qu'en numérique c'est a – 1 = 16,32 …) |
y = |
|
|
|
Pythagore dans le triangle
Ax |
b² = |
|
|
|
|
b = |
|
|
|
Pythagore dans le
triangle Ay |
c² = |
|
|
|
|
c = |
= 16,41… |
|
|
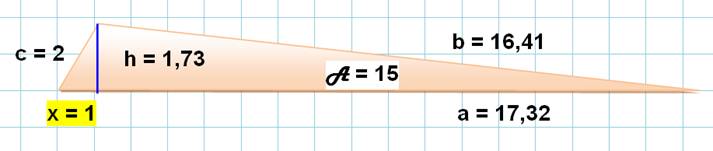
Illustration à l'échelle
|
|||
|
|
|||
|
Demi-périmètre |
s = |
½ (a + b + c) = ½ (17,32 + 2 + 16,41) = 17,865 |
|
|
A² = |
s (s – a) (s – b) (s –
c) = 17,865 = 224,751496719375 |
||
|
Aire du triangle
|
A = |
14,99… OK! |
|
Merci
à Noël G. pour sa contribution
|
|
|||||||||||||||||||||
|
Problème Un
triangle quelconque d'aire A. Ses côtés
sont en progression arithmétique de raison d. Longueurs
des côtés a, b, c ? |
Longueurs des côtés: a = b –
d; b et c = b + d Aire selon la formule de
Héron: A² = s (s – a) (s – b) (s
–c) avec s = (a + b + c) / 2 =
3b/2 |
||||||||||||||||||||
|
Calcul de l'aire |
|
||||||||||||||||||||
|
Mise en équation |
|
||||||||||||||||||||
|
Solution positive Équation du second
degré |
|
||||||||||||||||||||
|
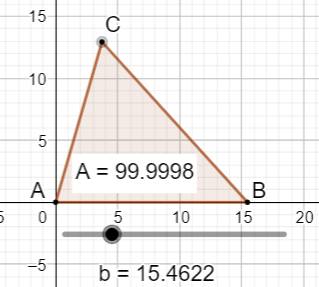
Exemple A = 100 et d = 2 b = 15,46216770689… On retrouve évidemment le cas des triangles
rectangles avec des nombres entiers comme: |
|
||||||||||||||||||||
|
Cas de nombres presque entiers |
|
||||||||||||||||||||
|
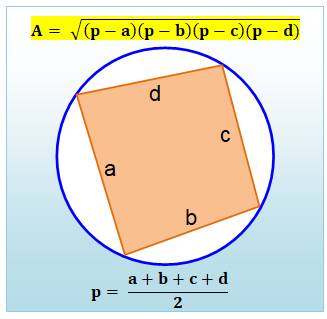
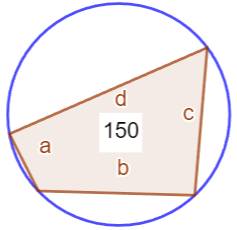
Propriété L'aire du quadrilatère inscriptible est égale à la
racine des produits des quatre différences entre p et la longueur des côtés. Sachant que p est le demi-périmètre. Exemple avec GeoGebra
Pour information: le cercle a un rayon de 10 unités. Le carré inscriptible aurait une diagonale de 20 unités
et son aire serait égale à 200. C'est la taille maximale du quadrilatère
inscriptible dans ce cercle. |
|
||
|
Démonstration
|
Voir |
||
Voir Aire
du quadrilatère circonscriptible / Aire
du quadrilatère inscriptible (doublon)
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/Heron.htm |
![]()