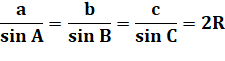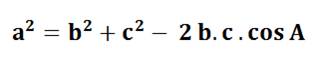NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Résolution				Glossaire Triangle
INDEX Triangle	Types de triangles	Résolution	Hauteur	Aire (Héron)
	Construction	Formules	Projection	T 13 14 15
	Isométriques	Hypoténuse		T 48°
		Sommaire de cette page >>> Index >>> Approche >>> Ce qu'il faut savoir

Résolution des TRIANGLES

Comment s'y prendre?

Avec un minimum de connaissances sur un triangle, comment trouver les autres mesures? Que le triangle soit particulier – équilatéral, isocèle, rectangle – ou quelconque.

Dans le cas du triangle quelconque, le recours à la trigonométrie est le plus pratique. Ne prenez pas peur, dans ce cas, il s'agit d'une simple consultation de votre calculette. Par ailleurs, Internet offre des calculateurs (résolveurs) de triangle. On peut s'en sortir sans trigonométrie en dessinant une hauteur et en utilisant le théorème de Pythagore.

Anglais: solving triangles

Index RÉSOLUTION du Triangle

Par rubriques principales

Général

Le triangle: types, droites remarquables, …

Triangles égaux (congrus)

Triangles semblables

Construction des triangles

Pré-requis

Ce qu'il faut savoir pour résoudre un triangle

Formules et lois dans le triangle

Formule de Héron – Calcul de l'aire

Longueurs des côtés (L) et Angles (A)

	3 côtés	2 côtés
	LLL	LAL	LLA
Quelconque	>>>	>>>	>>>
Rectangle	>>>	>>>	>>>
Isocèle	>>>	>>>	>>>
Équilatéral	>>>	>>>	>>>

	1 côté		Aucun côté
	ALA	AAL	AAA
Quelconque	>>>	>>>	>>>
Rectangle	>>>	>>>
Isocèle	>>>	>>>
Équilatéral	>>>	>>>

Résoudre le triangle à trois côtés de mesures consécutives

Hauteur

La Hauteur

Rectangle

Particulier

Résoudre le triangle rectangle en connaissant l'aire et le périmètre

Approche
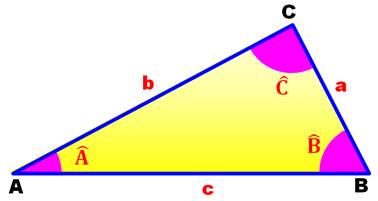
Dans un triangle, il ya six éléments de base les trois côtés et les trois angles. D'une manière générale, il suffit de connaître trois mesures pour en déduire les trois autres. Sauf, un cas!	Notations dans le triangle Six grandeurs: a, b, c,

Cas où les trois angles sont connus (AAA)
La figure montre que, si trois angles sont définis, il est possible de construire une infinité de triangles. Ceci est vrai quel que soit le type de triangle, bien sûr. Le triangle équilatéral est un exemple typique. Il en existe une infinité et pourtant, à chaque fois, on connait les trois angles, égaux à 60°. De tels triangles avec leurs angles égaux deux à deux sont dits semblables . Voir Méthode de construction	Seuls les angles sont connus Ces triangles ont les mêmes angles. Impossible de donner la longueur des côtés. Alignés de la sorte, ces triangles sont propices à l'emploi du théorème de Thalès

Ce qu'il faut savoir
Inégalité triangulaire	a + b > c La somme des longueurs de deux côtés est supérieur à la longueur du troisième côté. >>>
La somme des angles du triangle.
Loi des sinus
Loi des cosinus (exemple avec a)
Théorème de Pythagore	Si le triangle est rectangle en C a² + b² = c²

Suite	Formules pour résoudre les triangles Résolution des triangles LLL Constructions élémentaires: les triangles Résolution d'un triangle rectangle et 48°
Voir	Triangles héroniens Triangle – Introduction Triangle – Index Volume du tétraèdre Formule de Héron pour le trapèze Les dix problèmes d'Apollonius
Sites	Triangle calculator – Calculator.net – Vous donnez trois valeurs; il vous indique les trois autres et en prime le dessin du triangle. Calculateur de triangles – TrianCal
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/Resol.htm