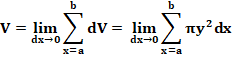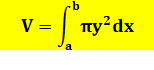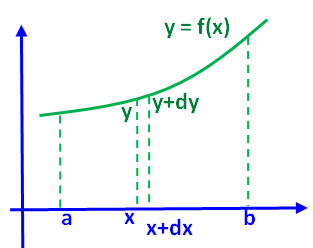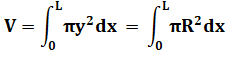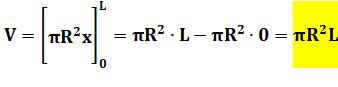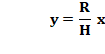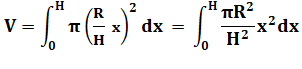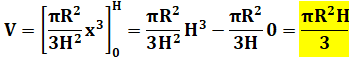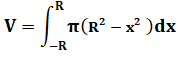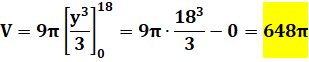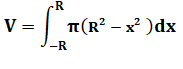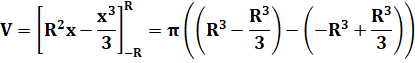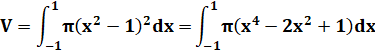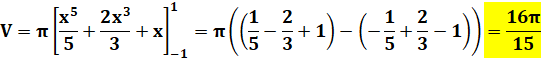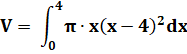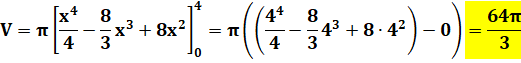|
Édition du: 30/07/2023 |
|
INDEX |
Types de Nombres – Motifs |
|||
|
Introduction
& index |
||||
Faites un double-clic pour un retour en haut de page
|
Volume des solides de révolution Formule
générale pour tout solide de révolution autour d'un axe (ici, l'axe des
abscisses). Cette
page s'applique à une rotation autour de l'axe des x. Pour une rotation autour
de l'axe des y, il faut simplement intervertir x et y. |
||
|
Terminale |
Sommaire de cette page >>> Volume d'un solide de révolution >>> Volume du cylindre >>> Volume du cône >>> Volume de la sphère >>> Volume de cette forme parabolique >>> Volume de cette forme en boucle >>> Volume de cette forme proche de la boucle |
Débutants Glossaire |
|
Solide défini par une fonction Le solide est défini par une fonction y = f(x). Le volume est limité par les des abscisses a et b. Mode de calcul Le principe consiste à découper le volume en fines
tranches et à ajouter leurs volumes. L'épaisseur de la tranche est dx entre x et x + dx, et son
amplitude de y à y + dy. Plus la tranche est fine (tendant vers zéro), plus il est
légitime d'assimiler y + dy à dy. Alors, le volume de la tranche (du petit cylindre) est: Somme finie et intégrale La somme des tranches de a
à b s'écrit:
De cette somme de tranches discrètes, on passe à la somme
continue de tranches d'épaisseur tendant vers zéro:
Dès que l'on
connait la courbe définie par y en fonction de x, on sait calculer le volume
du solide de révolution engendré par la courbe tournant autour de l'axe x. |
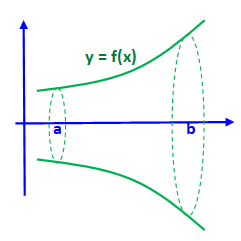
Solide de révolution autour de l'axe x
Définition du volume en dx et dy
|
|
|
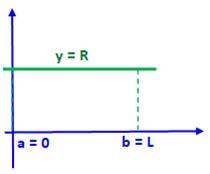
Cylindre droit de révolution Sa courbe de définition est une droite d'ordonnée
constante: y = R (le rayon du cylindre). Les limites du cylindre: a = 0 et b = L. Volume du cylindre droit de révolution
Passage à la primitive La primitive d'une constante est égale à x.
|
Remarque Le
fait que "y" est une constante permet un calcul simple: l'aire du
disque est simplement multipliée par la hauteur du disque pour obtenir le
volume. |
|
|
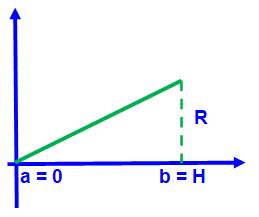
Cône droit de révolution Sa courbe de définition est une droite qui passe par 0 et par
le point (H, R). Son équation est: Volume du cône droit de révolution
Passage à la primitive La primitive de x² est:
1/3 x3
|
|
||||||||||
|
Exemple d'application Un cône de révolution autour
de y est formé avec la droite y = 1/3 x. La base du cône est un cercle de rayon 6 cm. Hauteur et volume du cône ? |
|
||||||||||
Voir Aire
latérale du cône et volume du cône
|
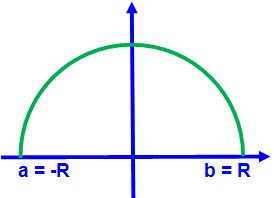
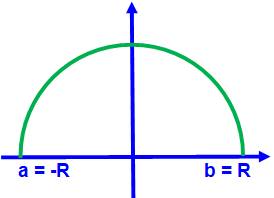
Sphère Sa courbe de définition est un demi-cercle Son équation est: Volume du cône
droit de révolution
Passage à la primitive
|
|
|
|
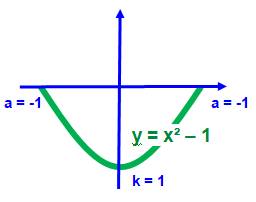
Solide Sa courbe de définition est un morceau de parabole Son équation est:
|
|
|
|
Passage à la primitive
|
||
|
Solide Volume engendré par cette boucle en rotation autour de l'axe
x. Son équation est: Limite
de la boucle: x = 4.
|
|
|
|
Passage à la primitive
|
||
|
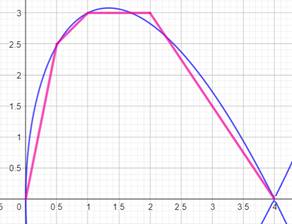
Solide Volume engendré par cette forme rose en rotation autour de
l'axe x. La forme est délimitée par quatre segments de droites dont
on calcule les équations, et on intègre de 0 à 1/2, de 1/2 à 1, puis de 1 à 2
et enfin de 2 à 4. Volume Le calcul donne un volume total: 119/6 π
= 19,83… à comparer à 64/3 π
= 21,33… π pour la
boucle ci-dessus. Calcul ci-dessous. |
|
|
|
Calculs
|
||
Haut de page (ou
double-clic)
|
Retour |
||
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
||
