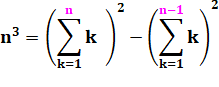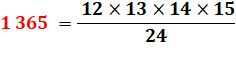NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/04/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES	Glossaire Nombres
1 10 100 500 / 600 700 / 800 900 / 1 000 1 100 1 200	1 300	1 400 1 500 / 1 900 2 000 / 3 000 5 000 10 000 20 000 100 000 10^6 / 10^9 / 10^100
	Mille trois cents ou treize cents Anglais: One thousand and three hundred

1 300

Transport

1 360 avions par jour (Rappel: Il ya 1440 minutes par jour) Cadence de l'aéroport d'Heathrow (Londres), le plus important d'Europe.

>>>

1 300	Nombre quadrillage.
1 300 = 1^5 + 2^5 + 3^5 + 4^5	Somme de puissance des nombres. Divisible par le nombre suivant 5; propriété générale. Voir Table

Géométrie

1 302 triangles dans un ennéagone et ses diagonales.

>>>

1 301	Nombre carré centré.
1 305 mod 30 = 15 1 305 mod 35 = 10 1 305 mod 51 = 30 1 305 mod 13 = 05 1 305 mod 130 = 5	Nombres modeste avec trois présentations. Le plus petit de type étendu. Les deux autres présentations sont triviales: les unités sont le reste de la division par 10.
1 306 = 1^1 + 3^2 + 0^3 + 6^4	Nombre triangulaire centré. Somme des puissances successives des chiffres.
1 308 nombres Romains	Quantité de nombres en chiffres romains écrit avec au plus six caractères.
	Plus petit nombre tel que, lui et ses trois suivants, ont trois facteurs distincts.
1 312	Nombre de Mian-Chowla. Nombre abondant primitif.

Physique

1 317 °C l'aimantation du fer disparaît à partir de cette température. L'agitation des aimants élémentaires, qui augmente avec la température, devient supérieure aux forces magnétiques entre ces aimants. Le phénomène est réversible quand on refroidit le matériau, l'aimantation réapparaît aux températures inférieures à la température de Curie.

>>>

1 320 = 10 x 11 x 12 1 320 = s(11, 9)	Nombre Tri Pronique. Nombres de Stirling 1. Nombre idonéal.
1 321	Nombre premier pointé.
1 323 = 3^3 ∙ 7^2	Nombre d’Achille.
1 324 1×3 + 3×2 + 2×4 + 4×1 = 21	Permutation des nombres 1 à 4 telle que la somme des produits (21) est minimale. Maximum pour 1243.
1 325	Nombre de Markov.
1 327	Nombre tarte.
1 327, 1 361	Premier écart égal à 34 entre premiers.
1 330 et 1 331	Paire de Ruth-Aaron.
1, 3, 3, 1	3^e ligne du triangle de Pascal.
1 331 = 11^3 = 111 + 113 + 115 + … + 131 = 66² – 55² = 4 356 – 3 025 = 666² – 665² = 443 556 – 442 225 1 331 11^11			Double palindrome. Cube à chiffres répétés. Somme des impairs successifs. Représentations élégantes de 1331 en différences de deux carrés. Ce sont les deux seules. Diviseur de 11^11 Voir Curieuses différences de deux carrés / Variations sur les carrés / Nombre 131
1 331 = 11^3 et 1 + 3 + 3 + 1 = 8 = 2^3			Cube doublement cube.
1 331k = 11k^3		Égalité valable pour tout k > 3. Ex: 13314 = 12510 et 114 = 510 dont le cube est 12510
121 = 11 x 11 = 121 1331 = 11 x 11 x 11 = 1331 14641 = 11 x 11 x 11 x 11 = 14641			Relations palindromes. Voir Nombre 11
			Seul cube, outre triviaux en 10 et 20, à être calculé sans faire intervenir la retenue.
1 331 = 11^3 = 10 x 11 x 12 + 11 = 1320 + 11 = 1331			Un cube est égal au produit du nombre par ses deux voisins plus le nombre >>>
1 331 – 1000 – 1 = 55 x 6			La différence entre deux cubes successifs moins 1 est divisible par 6. Propriété générale.
1 331 = (1 + 2 + …+ 11)² – (1 + 2 + … + 10)² = 66² – 55² = 11^3 = 4356 – 3025			Propriété
1 332 = 11^3 + 1^3 = 111 (11 + 1)			Somme de deux cubes avec coquetterie en 1.
1332 = 123 + 132 + … + 321 = 222 (1 + 2 + 3)			Somme des permutations des nombres formés des trois chiffres 1, 2 et 3.
(1 334) = (1 335) = 2 160			Doublet de nombres consécutifs ayant même somme de diviseurs. Voir 1 364
1 335			Nombre pentagonal.
1 335 = 1^2 + 2^2 + 2^3 + … + 14^2			Somme cumulée des puissances pures jusqu'à 196 = 14².

Langue

1 337 = LEET en langage leet. Remplacement des lettres par des nombres.

>>>

1 351² – 1 = 1 825 201 – 1 = 2^4 • 3^3 • 5^2 • 13^2		Septième nombre puissant en n² – 1. Liste: 3, 17, 26, 99, 485, 577, 1351, …
1 352 = 2^3 ∙ 13^2	Nombre d’Achille.
429 = 4 + 5 + … + 29 1 353 = 13 + 14 + … + 53		Somme qui reprend ses chiffres pour les extrêmes. Voir Nombre 429
1 359 x 7 = 9 513	Mêmes chiffres pour son septuple avec chiffres uniques (le plus petit).

Physique

1 361 W / m² Constante solaire. Éclairement énergétique de la Terre par le Soleil. Valeurs obtenues par les radiomètres modernes. Constante solaire: quantité d'énergie lumineuse frappant en une seconde une surface de 1 m² tournée perpendiculairement aux rayons solaires et située hors de l'atmosphère à la distance moyenne séparant le Terre du Soleil. Pionniers de cette mesure à partir de 1820: Claude Pouillet (1790-1868), John Herschel (1792-1871) et James Forbes (1809-1868).

>>>

1 362^1/2 = 36,90528417…		Les dix premiers chiffres sont pannumériques (le plus petit).
1 364 = 4^1 + 4^2 + 4^3 + 4^4 + 4^5		Somme de puissances de 4.
(1 364) = (1 365) = 2688		Doublet de nombres consécutifs ayant même somme de diviseurs. Voir 1 334
1 365		Nombre idonéal.
		Le produit de quatre nombres consécutifs est divisible par 24. Tous ces nombres figurent dans la cinquième diagonale du triangle de Pascal.
1 367		Primeval.
1 368 = 123 + 456 + 789 123 + 333 = 456 & 456 + 333 = 789 123 + 789 = 2 x 456 798 – 123 = 666		Somme des triplets de chiffres successifs (comme sur le clavier). Donc, partition pannumérique. Autre curiosités avec ces triplets.
1 369 = 37² et 1 = 1², 36 = 6², 9 = 3²		Carré concaténation de trois carrés.
1 369 = 37^2 1 936 = 44^2		Motif avec permutation des chiffres.
1 369 = 37² = 1^3 + 3^3 + 5^3 + 7^3 + 10^3		Carré somme de cubes.
1 372 = 2^2 ∙ 7^3		Nombre d’Achille.
1 375, …, 7513		Plus petit nombre formé des chiffres impairs et divisible par 11. Il y en a 8.
1 375 = 5^3 x 11 1 376 = 2^5 x 43 1 377 = 3^4 x 17		Trois nombres successifs avec des cubes.
1 376		Nombre abondant primitif.
1 379		Nombre tarte.
1 379 = 14 (14² + 1) / 2 = 197 x7		Constante du carré magique d'ordre 14.
1 379 3, 7, 13, 17, 19, 31, 37, 71, 73, 79, 97, 137 139, 173, 179, 193, 197, 317, 379, 397, 719, 739, 937, 971, 1973, 3719, 3917, 7193, 9137, 9173, 9371.		Nombre primeval: il contient 31 nombres premiers.
1 385	Nombre sécant.
1 385 = Qe(8)	Quantité de permutations d'Euler avec 8 termes.
1 386 x 6 = 8 316	Mêmes chiffres pour son sextuple avec chiffres uniques (le plus petit )
1393² = 2 × 985² – 1	Motif carré en 2n² + 1.
1 394 partitions du nombre 65	Avec les nombres de 1 à 25 sans répétitions. Avec les nombres de 1 à 15, seulement une partition: 11 + 12 + 13 + 14 + 15 = 65. Aucune pour 1 à moins de 15.
1 395	Nombre de Mian-Chowla.
1 395 = 15 x 93 1 435 = 35 x 41	Nombres de Friedman multiplicatifs, le plus petit à quatre chiffres et le suivant.
1 396	Nombre triangulaire centré.

Suite	Nombres 1 400
Voir	Nombre Chanceux Semaine Palindrome Triangle Tectroèdre Raisonnement Rep Unit Suites Nombre Têtus
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N1300.htm

Quelques repères dans ces pages >>> NOMBRE 1 331 Différence de carrés >>> NOMBRE 1 379 Primeval

>>> TEMPÉRATURE DE CURIE >>> SOLEIL