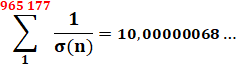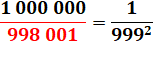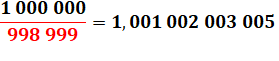NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/11/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Général	DicoNombre NOMBRES			Glossaire Général
1 10 100 1000 10 000 100 000 400 000 500 000 600 000	800 000 à 999 999			10^6 10^7 10^8 / 10^9 10^10 / 10^20 10^100
	Huit cent mille Anglais: Eight hundred thousand
800 000		900 000	999 999

800 000

Biologie	800 000 L'arbre de vie a-t-il une structure fractale? La lignée humaine pourrait connaître un saut majeur dans 800 000 ans.	>>>
Roman	802 701 Année du roman-fiction de H.G. Wells, La machine à explorer le temps.	>>>

	Exemple de nombre en numération romaine. Le viniculum (barre de surlignement) multiplie la valeur par mille.
823 543 = 7^7	Exemple de calculs avec le petit théorème de Fermat. >>>
823 550 = 7 + 7^7	Suite n + n^n.
844 844^6 = 363 629 530 013 266 201 512 325 739 310 125 056	Aucun chiffre en commun dans le nombre et sa puissance 6. Record.
853 615 = 58^3 + 87^3 = 5 587 (58 + 87)	Somme de deux cubes avec coquetterie.
857142 / 3 = 285714	Nombre, qui divisé par 3, voit son chiffre de queue (2) passer en tête.
873 612 = 1^1 + 2^2 + 3^3 + 4^4 + 5^5 + 6^6 + 7^7	Nombre hypertriangulaire Somme de puissances.
875 568 = 986 x 888	Multiplication comportant quinze fois le chiffre 8, en incluant les produits intermédiaires. Nombre en U (décroissant puis croissant).
888 888 = 7 x 126 984	Repdigit et produit, tous les chiffes du produit étant différents

900 000

900 901 ≅ Googol		Interprétation en langage Leet. Rappel: Googol = 10^100.
904 631	Deuxième plus petit pseudo-premier de Perrin.
904 523	Première suite de six décimales de e = exp(1) qui forment un nombre premier.
909 090	Nombre possédant 128 diviseurs, un record. Quantité de diviseurs des nombres en 9 Voir Divisibilité des nombres à chiffres répétés / Repdigits

912 574 = 9 + 122 + 5777 + 40000 + 866666	Motif: ABCDEF = A + BCC + DEEE + FGGGG + HIIIII – Alphamétique par Matthieu Dufour
933 458	Nombre méandrique.
946 669	Premier minimal.
2^948736 = … 9512948736	Cette puissance de 2 se termine par la valeur de son exposant.

952 952 = 17! / (6! x 6! x 6!)	Division de factorielles.
	Le cumul de la somme des inverses des diviseurs des nombres jusqu'à ce nombre passe le seuil du nombre entier 10.
		Trois nombres consécutifs ayant les mêmes chiffres dans la somme de leurs diviseurs (sigma).
966 291 = 2^3 + 3^3 + 5^3 + …+ 61^3	Somme des cubes de 18 premiers consécutifs.
969 969 = 2 x 3 x 5 x 7 x 11 x 13 x 17 x 19 / 10	Palindrome en 6 et 9, produit des huit plus petits nombres premiers divisé par 10.
970 299 = 99^3 = 98 x 99 x 100 + 99 = (100 – 2)(100 – 1) 100 + 99 = 10 000 – 300 + 1 + 99 = 970 299	Un cube est égal au produit du nombre par ses deux voisins plus le nombre >>>
978 121,99999948…	Multiple proche d'un entier.
978 405 = 1^6 + 2^6 + … 9^6	Somme des puissances 6 des nombres de 1 à 9.
978 460 = 9^3 + 7^3 + 8^3 + 4^3 + 4^3 + 0^3 + 9^4 + 7^4 + 8^4 + 4^4 + 4^4 + 0^4 + 9^6 + 7^6 + 8^6 + 4^6 + 4^6 + 0^6	Nombres narcissique généralisé.
982 827 = 98^3 + 28^3 + 27^3 983 221 = 98^3 + 32^3 + 31^3	Sommes des cubes avec ses chiffres.
987 654 = 6 x 164 609	Nombre divisible par 2 et 3 dont les chiffres se suivent. Divisible par 6. En retirant les chiffres par la droite, ces nombres sont divisibles par 5, 4, 3, 2, 1
987 917² = 975 979 998 889 et 9+7+5+9+7+9+9+9+8+8+8+9 = 97	Somme maximale atteinte par les chiffres d'un carré d'un nombre à six chiffres.
989 353^3 = 968 397 868 897 889 977 et 9+6+8+…+9+7+7 = 136	Somme maximale atteinte par les chiffres d'un cube d'un nombre à six chiffres.

990 009 = 999 x 991	Multiplication comportant quinze fois le chiffre 9, en incluant les produits intermédiaires.
990 100 = 990² + 100²	Motif singulier par concaténation.
998 001 = 999²	Multiplication en pyramide des repdigits.
998 001 = 999² = 90² + 99² + 990² = (100 – 10)² + (100 – 1)² + (1000 – 10)² = (1000 – 1)²	Carré somme de trois carrés, différences de nombres en progression géométrique (1, 10, 100, 1000). Propriété générale.
		Tous les nombres jusqu'à 999, sauf 998. Voir Nombre de Lewis Carroll
		Suite de Fibonacci jusqu'à 610. Le suivant est 987.

Multimédia

995 200 pixels ( 1 million) Résolution des photos numériques en 1998.

>>>

999 998 = 2 x 31 x 127²

Explique le motif de racine de 62 >>>

999 999

Facteurs	999 999 = 1 x 3^3 x 7 x 11 x13 x 37
Diviseurs	1, 3, 7, 9, 11, 13, 21, 27, 33, 37, 39, 63, 77, 91, 99, 111, 117, 143, 189, 231, 259, 273, 297, 333, 351, 407, 429, 481, 693, 777, 819, 999, 1001, 1221, 1287, 1443, 2079, 2331, 2457, 2849, 3003, 3367, 3663, 3861, 4329, 5291, 6993, 8547, 9009, 10101, 10989, 12987, 15873, 25641, 27027, 30303, 37037, 47619, 76923, 90909, 111111, 142857, 333333, 999999
Quantité	64
Somme	2 042 880
S – N	1 042 881

impair

composé

repdigit

nombre de Kaprekar

Voir Nom des nombres

Nombres géométriques

999 999 = 142 857 x 7			Produit avec nombre têtu.
999 999 = 999 998 + 000001 999 999² = 999 998 000 001			Magie valable pour tous les repdigits en 9 >>>
999 999 = 7 x 11 x 13 x 27 x 37 = 10^6 – 1			Égalité propice à un motif peu banal. Voir Nombres en N/999…
999 999 = 37 x 27 027 = 27 x 37 037			Curiosité Voir Fraction cryptarithme
…1134999999837…	Succession de six 9 dans Pi en 763^e position (en comptant le 3 initial), dit point de Feynman. Anecdote: Richard Feynman (1918-1988) aurait déclaré que connaissant 380 décimales de pi, il aurait souhaité pousser jusqu'à ce point terminant par des 9, et laissant penser à l'auditoire que la suite des 9 se poursuivait et que Pi est un nombre rationnel. Rapportée par Douglas Hofstadter
999 999^3 = 99999 7000002 999999		Son cube contient onze "9". Le plus petit cas. Voir Nombre 998
				Curiosité.

Suite	Nombres 1 000 000
Voir	Nombre Chanceux Semaine Palindrome Triangle Tectroèdre Raisonnement Rep Unit Suites Nombre Têtus
Site	Point e Feynman – Wikipédia Feynman Point – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N800000.htm