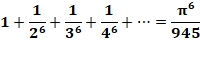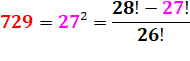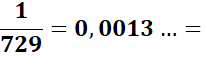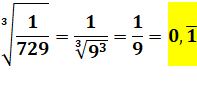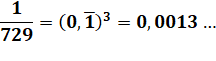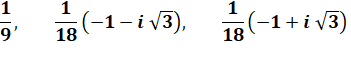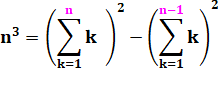|
Édition du: 22/02/2025 |
![]()
|
|
· Sept-cent-vingt-neuf. ·
Seven hundred and twenty-nine. |
||||||||||
|
·
Composé · Curzon · Forme (2k+1)² · Friable
(3-friable) · Friedman · Frugal · Puissant · Smith · Octogonal
centré (14e) |
Puissances de 6 et somme de leur
inverse
|
16 |
26 |
36 |
46 |
56 |
|
1 |
64 |
729 |
4 096 |
15 625 |
|
|
||||
|
·
Seule
heure cube: 729 = 93. |
||
|
·
729 Nombre
appartenant au Soleil selon Plutarque.
Œuvres morales de Plutarque, Volume 5 |
Chiffres et numération
|
729 = 27² & 7 + 9
= 16 = 4² |
· Carré dont la somme
des chiffres extrêmes est un carré. |
||
|
72 + 9 = 81 = 34 |
· Devient bicarré en
ajoutant une combinaison des chiffres. |
||
|
729 = 36 = 1
000 0003 |
· Un million en base
3. |
||
|
729 = 83 +
3x8² + 3x8 + 1 = 13318
= 26² + 2 x 26 + 1 = 12126 |
· Palindrome
en base 8 et en base 26. |
||
|
729 = 36 = 93 = 27² |
· Trois puissances.
Tout nombre carré
et cube à la fois est de la forme 7k ou 7k + 1. |
||
|
|
· Nombre de Friedman:
égal à une opération sur ses chiffres. |
||
Addition – Partition
|
729 =
93 = 73 + 75 + … + 89 |
· Somme d'impairs consécutifs. |
|
|
729 =
T26 + T27 = 351+ 378 |
· Somme de deux
nombres triangulaires. |
|
|
729 =
45² – 36²
= (36 + 9)² –
36² |
· Motif
général pour les cubes. |
|
|
729 = 364 + 3652 = 242 + 243 + 2443 |
· Le plus petit
nombre 6-polis, six fois somme de consécutifs. |
|
|
729 = 27² = 1 + 3 +
5 +…+ 53 |
· Le carré de n est
la somme des n premiers
impairs. |
|
|
729 = 45² – 36² = 27² =
9² x 3² |
· Nombre
complètement
carré. |
|
|
729
= 3652 – 3642 = 93 x 13 |
·
Différence
de carré = produit de cubes. |
|
|
729
= 14 + 15 + … 40 |
· Une
des six sommes de nombres consécutifs >>> |
|
|
729 = 1 + 8 + 16 + 64 + 128 + 512 |
· Puissance
de 3, somme de puissances de 2 distinctes. |
|
|
729 =
93 = 13 + 63
+ 83 = 13 + 33 + 43 + 53
+ 83 |
· Cube, Somme
de trois cubes
(ou de deux cubes à une unité près). Précédent du même type: 216. · Somme de cinq cubes
du fait que 63 est la somme de trois cubes. |
|
Multiplication et division
|
729 = 93 =
(2 + 3 + 4)3 = 8 x 9
x 10 + 9 =
720 + 9 = 729 |
· Un cube est égal au
produit du nombre par ses deux voisins plus le nombre >>> |
|
|
· Carré
= cette relation entre factorielles
successives. |
|
729 Diviseurs: {1, 3, 9, 27, 81, 243, 729} 7 + 2 + 9 = 3+3+3+3+3+3 = 18 7x2x9 = 126 et 126/18 = 7 |
· Nombre de Smith. · Produit des
chiffres (126) divisible par la somme des chiffres des facteurs (18). |
Inverse de 729
|
|
|
|
|
La
période de ce nombre
périodique est 81. En arrangeant les chiffres par rangées de neuf, les
trois premiers offrent une certaine régularité. La fin de période est
en 31, alors que le début est en 13. Ce qui offre un palindrome
à la jointure: …310013… |
001 371 742 112 482 853 223 593 964 334 705 075 445 816 186 556 927 297 668 038 408 779 149 519 890 260 631 |
|
|
Relation
avec 1/9
|
Les
trois racines de x3 =
1/729:
|
|
Voir Nombre
0,1111…
|
· Relation
croisée entre la somme des diviseurs et le totient. |
||||||
Puissance
|
729 = 27² =
13 + 33 + 43 + 53 + 83 |
|||
|
|
· Suite
infinie de carrés
avec des nombres en 266…667 V. Thébault- 1943 · Ces sortes de suites sont très
nombreuses. Exemple de multiplication
posée => |
|
|
|
729 =
(1 + 2 + …+ 9)² – (1 + 2 +
… + 8)² = 45² – 36² = 93 |
|
||
|
729 =
33 x 33 |
· Nombre à motif
ab . ba. |
||
|
729 =
3.33
+ 3.63 = 1.93 =
3(33 + 63) = 93 = 3
x 35 = 36 = 93 |
· Exemple de l'égalité
de Fermat. |
||
|
|
· Seul nombre dont la
différence entre la racine carrée et la racine cubique vaut 18. Calcul proposé au calculateur prodige Giacomo
Inaudi. Un
truc: comment
calculer la racine cubique de 729? D'abord factoriser en remarquant que 729
est divisible
par 9: 729 = 9 x 81 = 9 x 9 x 9 et le tour est joué! |
||
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
|
||
|
Extrait de La République de Platon ou
dialogue sur la justice de Platon Socrate: Le tyran est le troisième, à compter depuis l'oligarchie, car le
démocratique est entre les eux (…) Le tyran est donc éloigné du vrai plaisir
le triple du triple. Glauc: Oui, ce me semble. Socrate: Par conséquent le fantôme de plaisir du tyran,
à le considérer selon sa longueur, peut être exprimé par un nombre plan. Glauc: Oui. Socrate: Or, en multipliant
cette longueur par elle-même, et l'élevant à la troisième
puissance, il est aisé de voir combien le bonheur du tyran est éloigné
de la vérité. Glauc: Rien n'est plus aisé
pour un calculateur. Socrate: Maintenant, si l'on
renverse la progression, et qu'on
cherche de combien le plaisir du roi est plus vrai, on trouvera, le calcul
fait, que le roi est sept cent vingt-neuf fois
plus malheureux que le tyran, et que celui-ci est plus malheureux dans la même
proportion. Glauc: Vous venez de
trouver par un calcul tout à fait surprenant l'intervalle qui sépare le
bonheur du juste et celui de l'injuste. |
Explication selon l'auteur de la traduction en 1752 Le bonheur du tyran a trois fois mois de réalité que celui de
l'oligarchique. Celui de l'oligarchique en a trois
fois moins que celui du roi. Le bonheur du tyran a donc neuf fois moins de réalité que celui du roi. Le nombre neuf est un nombre plan,
puisque c'est le carré de trois. Platon considèrent ces deux
bonheurs, l'un réel et l'autre apparent,
comme deux solides dont toutes dimensions sont proportionnelles. En partant de la proportion de 9 en
longueur, il trouve que le bonheur du tyran est 729
fois moindre que celui du roi. Notez la manière
d'écrire en 1752
|
|
Voir Nombre de Platon 12 960 000
![]()
|
Suite |
Voir Haut
de page / Autres nombres |
|
Voir |
|
|
Cette page |
![]()