|
555
555 / 5 = 111
555 = 5 mod 55
|
5-repdigit
Divisible par chacun de ses chiffres.
Opération modulo avec ses chiffres.
|
|
555: 5 + 5 = 10 et 2 x
5 = 10
|
Somme des chiffres symétriques = 10.
|
|
555 = 3 x 5 x 37
357 =
sigma'(555)
|
Mêmes chiffres dans la factorisation et la somme des diviseurs
stricts.
|
|
555 => 5 + 5 = 10 et
5 + 5 = 10
|
Nombre palin10:
les chiffres symétriques complémentent à 10.
|
|
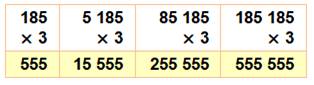
555 = 3 x 185
555 555 … = 3 x 185 185 …
444 444… = 6 x 74 074 …
888 888 …= 6 x 148 148 …
56 56 … = 7 x
79365 079365 …
59 59 … = 9 x
61728395 061728395 …
|
 Seuls cas où le
triple est un repdigit
fait de ses unités.
Voir cette Énigme
Autres multiples avec cette propriété
Notez
que tous les repdigits à quantité paire
de chiffres sont divisibles par 11 avec la même unité: 1111 = 11 x 101.
|
|
555 = 104 +
041 + 410
= 113 + 131 + 311
= 122 + 221 + 212
= 203 + 032 + 320
= 500 + 005 + 050
|
Sommes des permutations
circulaires des chiffres.
|
|
555 {113, 122, 500, 555}
|
Somme de toutes
les permutations des chiffres de chacun de ces nombres
|
|
555 = 4 +
5 + … + 32 + 33
555 = 30 + 31
+ … + 43 + 44
|
Repdigit:
somme d'entiers consécutifs.
Deux des sept sommes de nombres
consécutifs >>>
|
|
555 = 3 x 5 x 35
= 3 x 185
= (5 + 5 + 5) x 35
|
Nombre sphénique.
Repdigit
et produit, tous les chiffes du produit étant différents.
Nombre de Harshad.
|
|
555 / 15 = 37
|
Plus petit
multiple de 15 à être un repdigit. C'est le seul et il est en 5.
|
|
|
Motif qui se répète sans fin.
Il en existe bien d'autres comme
148
x 3 = 444 ou 148 = 6 = 888 …
Voir Repdigits
partiels
|
|
555 = 26² – 11² = 58² –
53² = 94² – 91² = 278² – 277²
|
Nombre binomial.
|
|
|
|
|
|