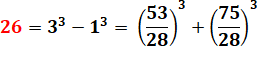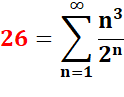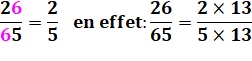|
Édition du: 04/03/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
Maths générales du
26 |
Maths détaillées du 26 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||
|
|
|||
|
Caractérisation
du nombre
|
|
Voir |
|
Rappel Propriétés générales >>>
Chiffres et numération
|
26 =
2 mod 6 |
|
|
26 +
62 = 88 62
– 26 = 36 = T3 |
|
|
26
= 1+7+5+7+6 |
Somme des chiffres de sa puissance 3. |
Addition et soustraction
|
p(26) = 2 436 |
|
|
26 =
5 + 6 + 7 + 8 |
|
|
26
= 3 + 5 + 7 + 11 |
|
|
26 = 5
+ 8 + 13 |
|
|
26
= 1 + 2 + 11 + 12 = 1 + 3 +
10 + 12 = … = 5 + 6 + 7 + 8 |
|
Multiplication, division, diviseurs
|
26
= 2 x 13 62 = 2 x 31 |
|
|
|
26 = 1210 – 1184 |
|
|
|
|
|
|
|
Σ λ(26)
= 0 |
|
|
|
Nombres
premiers |
|
|
Avec les puissances
|
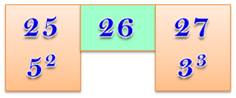
25 = 5² 26 27 = 33
|
De
même 8 = 23 et 9 = 32 sont deux nombres cube et carré consécutifs. Découverte
de Fermat
qu'il démontra au prix d'un raisonnement fort complexe. Il annonce la
propriété et met les mathématiciens de l'époque au défi de trouver la
démonstration. Wallis et Digby, deux mathématiciens anglais, durent s'avouer
vaincus. |
|
26 = 1² + 5²
= 1² + 3² + 4² =
2² + 2² + 3² + 3² |
|
|
26
= 2² + 2² + 3² + 3² |
|
|
26
= 1² + 5² = (1² + 1²) (2² + 3²) = 3² + 3² + 2² + 2² |
|
|
26 = 33 –
1² =
27 – 1
= 353 – 207² = 42 875 – 42 849 |
Différence
entre un cube et un carré. |
|
26 =
13 + 13 + 23 + 23 + 23 |
|
|
|
|
|
|
Voir suite et explications en 26 en série. |
|
26
= 353 – 2072 |
|
|
26
= (7 – 2)² + (7 – 6)² |
|
En puissance
|
26² =
676 264²
= 69696 307²
= 94249 … |
|
|
|
26²
= 10² + 24² |
|
|
|
26² – 1 = 676 – 1
= 33 · 52 |
|
|
|
263
= 17 576 et 1 + 7 + 5 + 7 + 6 = 26 |
|
|
|
263 = 74² + 110² = 26² + 130² |
|
|
Dénombrement, jeux et curiosités
|
26 + 5 = 31 26 x 5 = 130 (26, 386, 3986,
39…986) |
|
|
|
26 = 4 (3×4 + 1) / 2 C'est:
n (3n + 1) / 2 pour n = 4 |
|
|
|
26 |
|
|
|
26 |
|
|
|
26 |
|
|
|
|
|
|
|
|
|
262728
= 29192 x 9 |
|
|
|
|
Décimales
|
26, 282
… = |
|
|
|
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 1, 0, 1, 0] 3, [2, 2, 2] 4,
[1, 2, 2] 5, [1, 0, 1] 6,
[4, 2] 7,
[3, 5] 8,
[3, 2] |
9,
[2, 8] 10,
[2, 6] 11,
[2, 4] 12, [2, 2] 13,
[2, 0] 14,
[1, 12] |
15,
[1, 11] 16,
[1, 10] 17,
[1, 9] 18,
[1, 8] 19,
[1, 7] 20,
[1, 6] |
3,
[2, 2, 2] 12,
[2, 2] 25,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
![]()