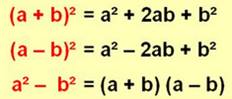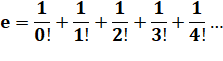NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/04/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Index général		Page 1 (1-19)		Page 2 (20-39)		Page 3 (40-59)		Page 4 (60-79)
	Page 5 (80-99)		Page 6 (100-119)		Page 7 (120-139)		Page 8 (140-159)		Page 9 (160-179)

BRÈVES de MATHS – Page 5

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

80. Divisibilité du produit de nombres
Deux nombres consécutifs 6 x 7 = 42 est divisible par 2. 7 x 8 = 56 est aussi divisible par 2. Parmi trois nombres consécutifs l'un est pair, alors: Le produit de deux nombres consécutifs est pair (divisible par 2). Trois nombres consécutifs 6 x 7 x 8 = 336 = 6 x 56 est divisible par 6. 7 x 8 x 9 = 504 = 6 x 86 est divisible par 6. Parmi deux nombres consécutifs, il existe un nombre pair (au moins) et un nombre divisible par 3 (éventuellement, le même). Le produit de trois nombres consécutifs est divisible par 2x3 = 6.		Plusieurs nombres consécutifs 6 x 7 x 8 x 9 = 3 024 = 24 x 126. 7 x 8 x 9 x 10 = 5 040 = 24 x 210 Parmi quatre nombres consécutifs, il en existe un divisible par, un divisible par 3 et un divisible par 4. Le produit est divisible par 2 x 3 x 4 = 24 = 4! Le produit de k nombres consécutifs est divisible par le produit des k premiers nombres (k!). Ce produit est nommé factoriel k et est noté avec un point d'exclamation: k! Exemple Ainsi, le produit de dix nombres consécutifs est divisible par 10! = 3 628 800. Ex: 5x6x7x…x 14 = 3 632 428 800 = 10! x 1001.
Pour en savoir plus	>>> Factorielle >>> Divisibilité de produits de nombres consécutifs >>> Nombre 10

81. Identités remarquables
Calcul mental 21² = 400 + 40 + 1 = 441 Simple! C'est 20² + 2x20x1 + 1² 12² = 100 + 40 + 4 = 144 Ouah! Les nombres comme les carrés sont retournés. Ok! Mais revenons au calcul … Identité remarquable (a + b)^2 = (a + b) (a + b) = a(a + b) + b(a + b = a^2 + 2ab + b^2 Application aux nombres à deux chiffres n = 10d + u (10 fois la dizaine plus l'unité). n² = (10d + u)^2 = 100d² + 20du + u² 21² = 100x2^2 + 20x2x1 + 1^2 Avec l'habitude 32² = 900 + 120 + 4 = 1024		Identités remarquables à connaître Pourquoi les connaître? Les applications sont très nombreuses et, en plus, au collège et au lycée, les exos sont souvent orientés pour les utiliser ! Sachez notamment reconnaitre la troisième. Elles sont, en quelque sorte, le théorème de Pythagore de l'arithmétique.
Pour en savoir plus	>>> Identités remarquables >>> Calcul mental des carrés		>>> Nombre 144 >>> Nombres carrément réversibles

82. Racine cubique jusqu'à deux chiffres
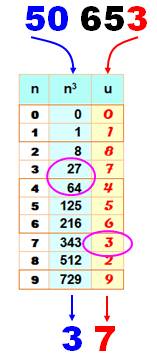
Nombres à un chiffre Comme le montre la table à droite: Les chiffres des unités sont identiques sauf pour 2, 3, 7 et 8 pour lesquels c'est le complément à 10. Exemples de calcul de racine 216 => chiffre des unités 6 => 216 = 6^3 512 => chiffre des unités 2, complément à 10 = 8 => 512 = 8^3 Nombres à deux chiffres On lit dans la table proposée, ou on apprend cette table par cœur. Unité: Comme pour un seul chiffre. 50 653 => 3 => 7 Dizaine: Prendre les milliers Lire le cube immédiatement inférieur dans la table. 50 => 27 => 3 La racine cubique de 50 653 est 37.			Exemple de calcul de racine cubique par lecture directe dans cette table
Pour en savoir plus	>>> Racine cubique >>> Racine carrée	>>> Cubes (nombres)

83. Équations et Racines – Un bon truc!
Développement Transformer un produit en somme		Factorisation Transformer une somme en produit
Produit Soit le produit algébrique suivant qui vaut 0. (x – 1) . (x – 2) = 0 La question que l'on se pose est: pour quelle(s) valeur(s) de x cette égalité (on dit équation) est satisfaite? Ici, la réponse est évidente: si je remplace x par 1, le premier facteur (x – 1) est nul (1 – 1 = 0) et le produit est nul; même chose avec x = 2. On dit que les racines (les solutions) de cette équation sont: x = 1 et x = 2 Développement de ce produit Nous savons calculer le produit avec parenthèses: (x – 1) (x – 2) = x.x – 2.x – 1x + (-1).(-2) = x² – 3x + 2 NB. la multiplication est noté par un point pour ne pas confondre avec l'inconnue x. Avec l'habitude, le point est même sous-entendu.		Somme Trouver les racines de l'équation suivante: x² – 3x + 2 = 0 Pas facile a priori ! Pourtant (voir à gauche), nous savons que x = 1 et x = 2 sont les deux solutions. 1² – 3.1 + 2 = 1 – 3 + 2 = 0 2² – 3.2 + 2 = 4 – 6 + 2 = 0 Le truc! x² – 3x + 2 = 0 Les deux coefficients ont des propriétés remarquables: le dernier (2) est le produit des racines et celui du milieu (-3) est leur somme. Factorisation d'une somme x² – 5x + 6 = 0 Dernier coefficient: 6 = 2 x 3 Coefficient central: - 5 = (-2) + (-3) Soit la factorisation avec ces deux racines (x – 2) (x – 3) = 0
Pour en savoir plus	>>> Équations – Introduction >>> équations qui affolent le Net >>> Équation du second degré		>>> Somme et produit >>> Factorisation avec le 3^e degré

84. Constante e = 2,718281828…
Constante d'Euler e En mathématique, cette constante est aussi importante que Pi. Elle est très utile notamment en physique et en économie (calcul des intérêts composés). Comme Pi, la constante e est d'une nature sophistiquée. Elle est: irrationnelle: n'est pas égale à une fraction; elle a une infinité de chiffres non répétitifs après la virgule; et transcendante: n'est pas racine d'une équation. Applications mathématiques La constante e est associée aux calculs des logarithmes et des exponentielles.		Identité d'Euler Vers 1748, Euler trouve cette relation extraordinaire entre cinq constantes mathématiques: Constante e (monde des croissances rapides); Constante Pi (monde des formes circulaires); Constante i (monde des nombres imaginaires) et les deux nombres 0 et 1. Du fait de son importance, cette identité est aux mathématiques ce que E = mc² est à la physique. Une manière de calculer la valeur de e Somme des inverses des factorielles des nombres successifs. Sachant que, par exemple, 4! = 1 x 2 x 3 x 4 = 24.
Pour en savoir plus	>>> Constante e >>> Constante Pi >>> Identité d'Euler >>> Nombres imaginaires >>> Leonhard Euler (1707-1783) >>> Relation E = mc²		>>> Nombre 0 >>> Nombre 1 >>> Factorielle >>> Logarithme >>> Exponentielle

85. Arrangements – Le tiercé
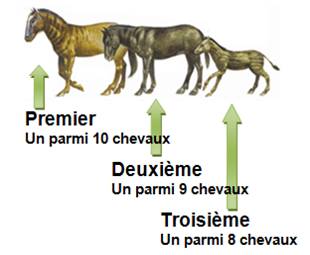
Dix chevaux sont au départ. On mise sur les trois premiers à l’arrivée. Combien de possibilités ? Dès que le premier a été choisi parmi les dix chevaux au départ, il en reste neuf qui sont susceptibles d’arriver en deuxième position, puis seulement huit pour la troisième place. Si le premier est connu, il y a donc 9 possibilités pour le suivant ; soit 10 x 9 possibilités selon celui qui arrive en premier. En tenant compte des 8 possibilités pour le troisième, c’est 10 x 9 x 8 = 720 possibilités de tiercés. Avec 20 chevaux, on aurait 20 x 19 x 18 = 6 840 arrangements de 3 parmi 20. Avec 20 chevaux, on aurait 20 x 19 x 18 x 17 x 16 = 1 860 480 arrangements de 5 parmi 20.
Pour en savoir plus	>>> Compter – Introduction >>> Principe multiplicatif		>>> Arrangements >>> Dénombrements

86. La chaine et ses maillons
Énigme Nous disposons de six morceaux de chaîne de quatre maillons chacun. Ouvrir un maillon coûte 1€ et souder un maillon pour le fermer coûte 5€. Quel est le coût pour former une seule chaîne avec tous ces morceaux ?		Solution Je coupe les 4 maillons d'un des morceaux de chaîne. Je dispose de 4 maillons ouverts.		4 x 1€
		Il reste 5 morceaux à réunir. J'utilise les maillons ouverts pour réunir les 5 morceaux. Et je les soude.		4 x 5 €
		Coût de l'opération et c'est la solution la plus avantageuse.		24 €
Pour en savoir plus	>>> La chaine		>>> Énigmes classiques >>> Jeux et énigmes

87. Diviseurs d'un nombre

Définition

Les diviseurs d'un nombre entier sont tous les nombres qui divisent ce nombre exactement, sans reste.

On compte le nombre 1 et le nombre lui-même parmi les diviseurs.

Ainsi, un nombre premier possède 2 diviseurs.

Exemple

12 est divisible par 2, par 3, par 4 et par 6, car: 12 = 2 x 6 = 3 x 4 = 4 x 3 = 6 x 2

Le nombre 12 est égal à 3 x 4, mais on peut encore diviser 4:
12 = 2 x 2 x 3 et, là, on ne peut plus diviser.

Les nombres 2 et 3 sont les facteurs ou diviseurs premiers de 12.

Fiche d'identité d'un nombre (exemple)

N	12
Facteurs	2 x 2 x 3 = 2^2 x 3
Diviseurs	1, 2, 3, 4, 6, 12
Quantité		6
Somme		28
Somme propre		16

Exposant

Lorsqu'un facteur intervient plusieurs fois, on place un exposant indiquant combien de fois il est présent.
360 = 2 x 2 x 2 x 3 x 3 x 5 = 2³ x 3² x 5

Puissance de 2

2⁵ = 32; ses diviseurs: 1, 2, 4, 8, 16, 32.
Somme des diviseurs propres: 63 = 2⁵ – 1

La somme des diviseurs d'une puissance de 2 est égale à cette puissance moins 1.

Pour en savoir plus

>>> Diviseurs et facteurs

>>> Nombres composés

>>> Nombre premier

>>> Nombre 12

88. Chiffres romains
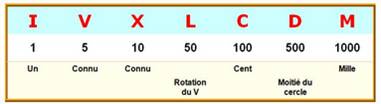
Les chiffres romains Autrefois mille était représente par un cercle barré. Le symbole 500 en garde la trace (demi-cercle). Compter de 1 à 11 L'addition des symboles est la règle générale, sauf pour le nombre juste avant le symbole. Dans ce cas, un symbole plus petit doit être soustrait. En bleu, une écriture tolérée à l'époque médiévale.		Utilisations principales de nos jours Nom de souverains Nom des siècles Montres et horloges Arrondissements Actes et scènes de théâtre Numéros de certaines pages dans les livres Jeux La représentation en bâtons donne lieu à de nombreuses énigmes. Exemple: il faut rétablir cette égalité sans toucher aux allumettes: Vous avez compris, il suffit d'effectuer un demi-tour et, l'égalité devient 10 = 1 + 9.
Brèves associées	>>> Numération romaine médiévale
Pour en savoir plus	>>> Numération romaine >>> Jeux avec les chiffres romains >>> Boulier – Abaque		>>> Nombre 100 >>> Nombre 1000 >>> Jeux et énigmes

89. Nombre 5 – CINQ
Propriétés Le nombre 5 est un nombre premier comme 2, 3, 7… En chiffre romain de 5 se représente par un V, figure formée par le pouce et le petit doigt. C'est un nombre de Fibonacci: 1, 1, 2, 3, 5, 8; nombres tels que chacun est la somme des deux précédents. Le nombre 5 est la somme des deux premiers nombres au carré: 5 = 1² + 2². Le produit de deux nombre terminés par 5 se termine par 5. Ex: 15 x 25 = 375. Divisibilité par 5 Un nombre est divisible par 5 s'il est terminé par 0 ou 5. Le produit de cinq nombres consécutifs est divisible par 5. C'est aussi le cas de la somme de cinq nombres en progression arithmétique. 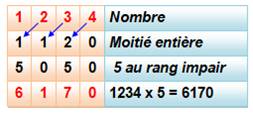Ex: 3 + 6 + 9 + 12 + 15 = 45 14 + 21 + 28 + 35 + 42 = 140		Multiplication par 5 Elle est simple: on multiplie par 10 et on divise par 2. Mais, voici une façon plus originale: Géométrie Une figure avec cinq côtés est un pentagone. Dans le pentagone régulier on peut dessiner une étoile à cinq branches. Cette figure recèle le nombre d'or. Devinette: 5 + 5 + 5 = 550 Comment rétablir l'égalité en ajoutant une seule barre? Il suffit d'ajouter une barre au signe plus pour faire un 4.
Brèves associées	>>> Nombre 4		>>> Nombre 6
Pour en savoir plus	>>> Nombre 5 – Culture >>> Nombre 5 – Maths >>> Nombre 5 – Quantité >>> Divisibilité par 5		>>> Multiplication par 5 originale >>> Nombre de Fibonacci >>> Pentagone >>> Nombre d'or

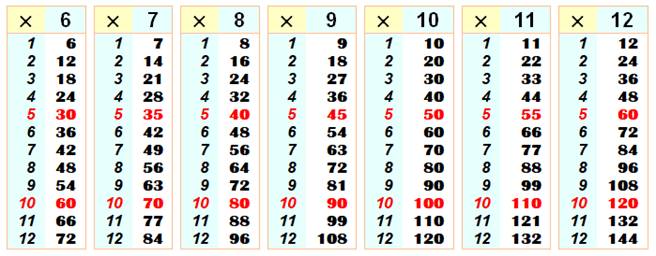
90. Tables de multiplication – de 6 à 12
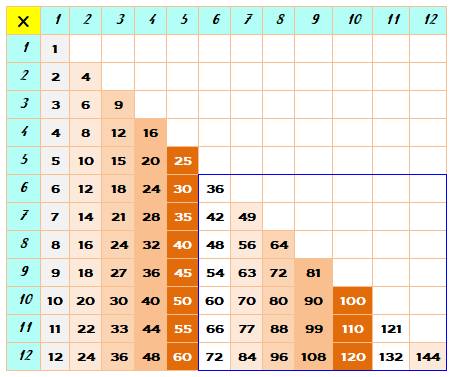
Point de situation Nous connaissons la table de 2 à 5. Il nous reste à connaître les 24 nombres du carré entouré de bleu. Table du 10 et du 11 (en ocre sur la table du bas) Voilà des valeurs simples à retenir. Remarquez que 11x12 = 1?2 et la somme (1+2) figure au centre 132. Carrés (en vert sur la table du bas) Il est utile de les connaitre par cœur: 6x6 = 6² = 36; 7x7 = 7² = 49; 8x8 = 8² = 64; 9x9 =8² = 81; 10x10 = 10² = 100; 11x11 = 11² = 121; et 12x12 = 12² = 144. Utilisez la méthode avec les doigts si nécessaire. Chaque carré est égal à son voisin bas-gauche, plus 1. Ex: 7 x 9 = 63 et 63 + 1 = 8²
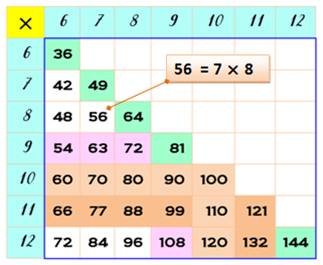
Table du 9 (en violet sur la table ci-contre) Rien de plus simple que la table du neuf: pour 8 x 9, par exemple: prenez 1 de moins (8 – 1 = 7) et complétez ce nombre à 9 (9 – 7 = 2). Résultat: 72. Utilisez la méthode avec les doigts si nécessaire. Fin de table (en blanc sur la table ci-contre) Remarquez la beauté de 56 = 7x8, quatre chiffres qui se suivent. C'est souvent la multiplication la plus difficile à retenir. On apprend par cœur les cinq multiplications qui restent.
Table conventionnelle
Brèves associées	>>> Table de multiplication de 1 à 5 >>> Multiplication par 9 avec les doigts				>>> Multiplication
Pour en savoir plus	>>> Table de multiplication >>> Multiplication >>> Calculette				>>> Carrés >>> Carrés avec les doigts >>> Table du 9 avec les doigts

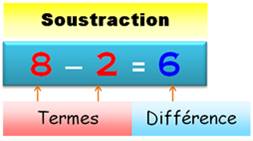
91. Soustraction de nombres entiers
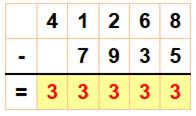
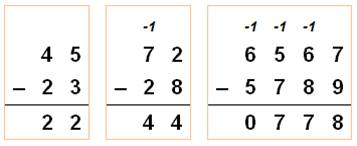
Principe En retirant des éléments d'une collection, combien en reste-t-il? Cette opération n'est possible que si la collection est plus grande que celle à retirer. Soustraction Amusement La différence est un nombre uniforme en 3 et les deux termes utilisent les neuf chiffres.		Soustraction posée On soustrait les chiffres colonne après colonne en commençant par la droite. Si le chiffre du haut est trop petit, on lui ajoute une dizaine en mentionnant ce fait par un -1 en haut de la colonne suivante (retenue). Soustraction en ligne 45 – 23 = 22 On ne peut pas inverser les termes La soustraction n'est pas commutative. Soustraction avec parenthèses 45 + 25 – 34 – (10 + 5) – (10 – 5) On effectue les calculs dans les parenthèses en priorité. = 45 + 25 – 34 – (15) – (5) = 70 – 34 – 15 – 5 = 16 Nombres négatifs S'il est difficile de retirer plus de 5 pommes dans une collection de 5 pommes, il est des domaines où c'est faisable. Avec 100 euros en banque, il est possible d'acheter un objet qui coûte 120 euros en créant un découvert de 20 euros. Oui! La banque ne va pas aimer. On note: 100 – 120 = – 20
Brèves associées	>>> Somme des nombres de 1 à n >>> Addition
Pour en savoir plus	>>> Soustraction >>> Opérations – Index		>>> Nombres négatifs >>> Nombres uniformes et pannumériques >>> Cryptarithmes

92. Théorème de Pythagore
Découverte Pythagore dessinait un triangle rectangle dans le sable et, rêvant, il dessine les carrés apposés aux côtés. Surpris, il constate que la somme des surfaces des deux plus petits égale celle du plus grand. En fait, les Chinois connaissaient déjà cette propriété. Démonstration Un petit carré inscrit dans un grand carré. 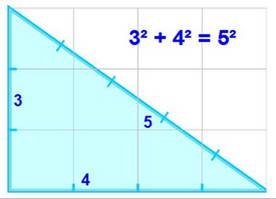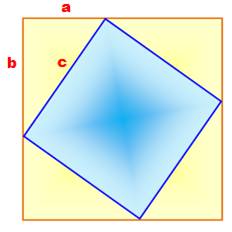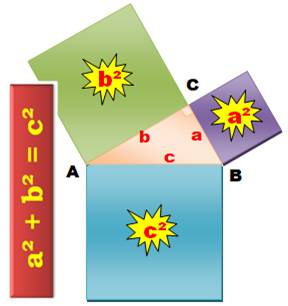Aire du grand carré: A = (a + b)² = a² + 2ab + b² Aire du grand carré par la somme des surfaces: A = 4 x (a.b) / 2 + c² = 2 ab + c² En comparant: a² + 2ab + b² = 2ab + c² En simplifiant: a² + b² = c² Triangle rectangle le plus célèbre (isiaque)		Le théorème de Pythagore en un dessin ABC est un triangle rectangle L'aire du grand carré bleu est égale à l'aire du carré vert plus celle du carré violet. Expression mathématique Les longueurs des côtés des carrés sont égales à celles des côtés du triangle rectangle (a, b et c). L'aire du carré est égale au carré de la longueur du côté. L'égalité de Pythagore s'écrit très simplement en fonction de (a, b et c) : a² + b² = c² Ce qui fait dire que, en revenant au triangle rectangle: Le carré de l'hypoténuse (c²) est égal à la somme des carrés des deux autres côtés (a² + b²). Applications Chaque fois qu'un triangle rectangle est présent; et s'il n'est pas présent, dessinez une hauteur!
Brèves associées	>>> Pythagore – Biographie >>> Triangle rectangle		>>> Triangle 3 – 4 – 5 >>> Triplets de Pythagore
Pour en savoir plus	>>> Théorème de Pythagore >>> Triangle isiaque		>>> Carré en géométrie

93. Mnémotechnique des chiffres
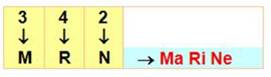
Origine En 1634, le Français Pierre Hérigone publie un ingénieux système pour mémoriser les nombres en passant par des mots: Les chiffres sont remplacés par des consonnes entre lesquelles on ajoute des voyelles pour formuler des mots du vocabulaire courant. Système vite adopté par de nombreux experts, dont Leibniz. Principe Je veux mémoriser mon code de casier à la piscine: 342. Les chiffres sont transformés en consonnes, puis en un mot en ajoutant des voyelles: Je forme la phrase clé: à la piscine, je me trouve dans la marine Le rappel consiste à isoler les consonnes M, R et N et à retrouver les chiffres correspondants.		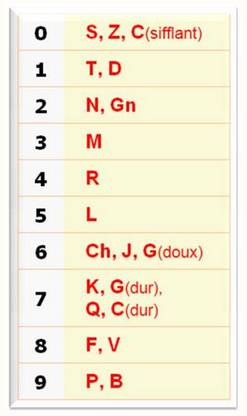Le code des chiffres Chacun trouvera la méthode pour retenir cette liste (le M a trois pattes, le R est le retourné du chiffre 4, etc.)
Pour en savoir plus	>>> Mnémotechnique des chiffres >>> Mnémotechnique – Index		>>> Mémoriser les départements

94. Mon tout premier programme

95. Réalisation de mon premier programme
Réalisation (Implémentation du programme) Avec Scratch: le logiciel disponible gratuitement et accessible immédiatement par tous. Le programme commence lorsqu'on clique sur le drapeau vert. On commence par effacer tout et on positionne le chat en bas à gauche sans écrire. On commande ensuite au stylo d'écrire en rouge avec une épaisseur de 3. Commencent alors les instructions de mouvement. Le chat est orienté vers le nord (0°) et il avance de 35 pas (valeur ajustée); il est orienté à l'est (90°) et avance de 35 pas. De tels mouvements sont ensuite commandés en demandant de les répéter quatre fois. Fin.				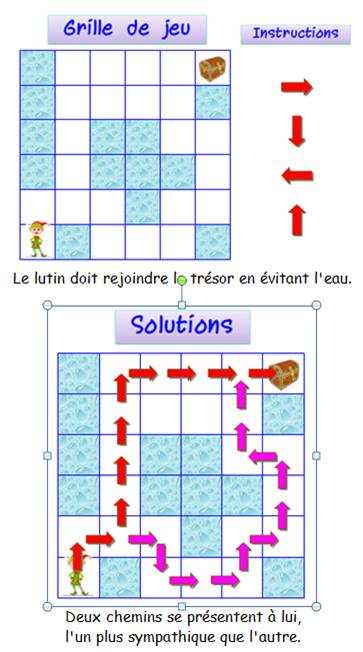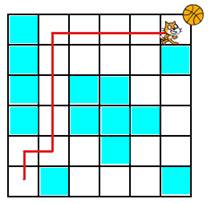L'exécution du programme de gauche a pour effet de déplacer le chat jusqu'au ballon en laissant la trace se son passage en rouge.
Pour en savoir plus	>>> Programmation – Débutant >>> Programmation – Index		>>> Programmation avec Scratch

96. La suite qui se lit
Énigme, dite du commentaire numérique ou suite de Conway ou encore suite audio-active Cette suite est particulièrement déroutante et même parfois difficile à faire comprendre. Question Quel est le nombre qui vient après cette suite de nombres? 1, 11, 21, 1 211, 111 221 ? Indice Les chiffres représentent deux choses différentes: la quantité de chiffres, suivi de la valeur du chiffre. 1, 11, 21, 1 211, 111 221, ? Solution Lisez à haute voix et écrivez au fur et à mesure: je vois un 1, j'écris 11. Maintenant, je vois deux 1, j'écris 21. Je vois un 2 et un 1, j'écris 1211. Je vois un 1, un 2 et deux 1, j'écris 111 221. Le suivant sera: 312211.		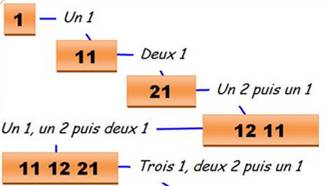Le principe de la construction Les dix premiers nombres de la suite Propriétés Les nombres grandissent inexorablement et pourtant elle reste formées de 1, 2 et 3; jamais de 4.
Brèves associées	>>> Suite de Kolakoski
Pour en savoir plus	>>> Suite du commentaire numérique >>> Suites classiques		>>> Jeux et énigmes >>> Nombre 1

97. Le carré
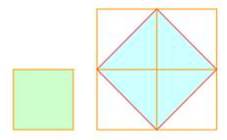
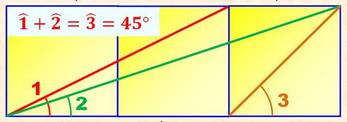
Définition Le carré est un quadrilatère dont les quatre côté sont égaux et les quatre angles sont droits. Caractéristiques Périmètre = 4a (avec a la mesure du côté). Aire = a² Diagonale = a 2 Il a quatre axes de symétrie. Comment doubler la surface du carré? Aire du carré vert: a² Aire du carré bleu: (a 2)² = 2a²		Le carré – Angles droits et axes de symétrie Curiosité
Brèves associées	>>> Périmètre et Aire
Pour en savoir plus	>>> Carré en géométrie		>>> Nombre 4

98. Premier en 6k+1 et 6k+5
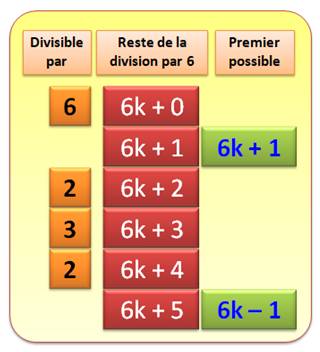
Un nombre premier n'est divisible par aucun nombre, à part lui-même et 1. La division par 6 En considérant la suite des nombres entiers, il y a ceux qui sont divisibles par 6. Ce sont les multiples de 6 que l'on note 6k (six fois un nombre quelconque k). Il y a ceux qui donnent un reste égal à 1. Ce sont les multiples de 6 plus 1. Notés 6k + 1. Ceux qui sont multiples de 6 plus 2, notés 6k + 2. Ceux-ci sont divisibles par 2. Comme ceux en 6k + 3, divisibles par 3 et en 6k + 4, divisibles par 2. Bilan, les nombres en 6k, 6k + 2, 6k + 3 et 6k + 4 sont composés. Seuls les nombres en 6k + 1 et 6k + 5 sont susceptibles d'être premiers. Exemple: 17 = 6x2 + 5 est premier, mais 63 = 6x10 + 3 est composé divisible par 3.		Tous les nombres premiers sont voisins d'un multiple de 6, sauf 2 et 3.
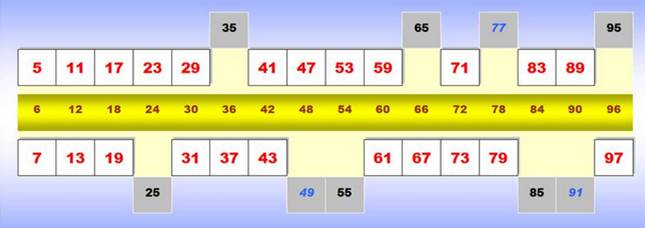
Barre magique des premiers En jaune les multiples et 6 au milieu; en rouge les nombres premiers de part et d'autre des multiples de 6; et, en extérieur, les voisins des multiples de 6 qui ne sont pas premiers. Cette barre constitue un excellent moyen pour retenir tous les nombres premiers entre 1 et 100. Ne pas oublier d'y ajouter les nombres 2 et 3.
Brèves associées	>>> Nombres premiers
Pour en savoir plus	>>> Nombres premiers en 6k+1 et 6k+5 >>> Barre magique des nombres premiers		>>> Autres formes possibles >>> Nombre 6

99. Lapins et canards
Problème Des lapins et des canards. Je compte des animaux: 15, et Je compte les pattes: 50. Combien de lapins et combien de canards?		Solution Je suppose que tous les animaux sont des lapins. Il y aurait alors 15 x 4 = 60 pattes. Or, il n'y en a que 50. Soit 10 pattes de trop. Je dois remplacer certains lapins par des canards. Chaque remplacement supprime deux pattes. Je dois faire 10/2 = 5 remplacements. C'est le nombre de canards. Il y a ainsi 15 – 5 = 10 lapins.
Pour en savoir plus	>>> Diverses énigmes de ce type >>> Énigmes pour juniors (diaporama)

Retour	Brèves de maths – Page 4
Suite	Brèves de maths – Page 6
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve05.htm