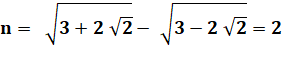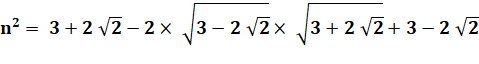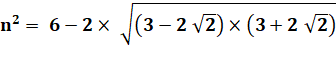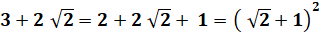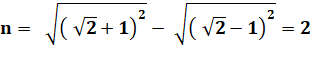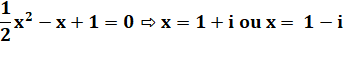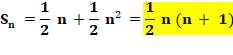|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 10 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
180. Calcul impossible? |
|
|||
|
Montrez
que: |
|
|||
|
1)
Calcul habituel |
Avec
élévation au carré: (a – b)² = a² – 2ab + b² |
|||
|
Au carré |
|
|||
|
Calcul |
|
|||
|
Identité remarquable |
|
|||
|
Racine carrée |
|
|||
|
2)
On aurait pu faire |
En
cherchant un carré sous le radical: |
|||
|
En remarquant que |
|
|||
|
Le calcul est immédiat |
|
|||
|
Pour en savoir plus |
>>>
Identités remarquables >>>
Calculs avec radicaux |
>>>
Nombre 2 >>> Calcul avec racines cubiques et quatrièmes |
||
181.
Théorème de la divisibilité
|
|
|||
|
Carl Friedrich Gauss (1777-1855), mathématicien et aussi physicien et
astronome. Il est l’auteur de ce théorème. Théorème Si
le nombre naturel a divise le produit b.c et s’il est premier avec l’un des
facteurs, alors il divise l’autre. |
Démonstration avec le théorème de Bézout Disons que a est premier avec
b.
|
|||
|
Brèves liées |
>>>Théorème de Bézout – B161 |
|||
|
Pour en savoir plus |
>>>
Divisibilité – Critères >>>
Lemme de la divisibilité >>>
Premiers entre eux |
>>>
Théorème de Bézout >>> Gauss
(1777-1855) |
||
182.
Base
12
|
|
|||
|
Nous
comptons en base 10, c'est-à-dire avec dix chiffres. Et, si on comptait avec
douze chiffres? L'idée s'est développée au cours des siècles. Pourquoi? Parce
que 12 est divisible par 2, 3, 4, 6; alors que 10 n'est divisible que par 2
et 5. Nos
Anciens trouvaient plus commodes de pouvoir partager les choses à partir de
12 parts. Voyez comme cette idée à résisté sur nos horloges et montres. Elle
résiste encore dans la vente des œufs, même si aujourd'hui on peut aussi
acheter ses œufs par dix. La
base 10 a dix signes à résisté sans doute parce que nous avons dix doigts.
Savez-vous que 1,7 bébé sur 1000 est atteint d'hexadactylie (six doigts aux
mains ou aux pieds) |
Quantité 12 = 1 douzaine Promotion: 13 à la douzaine 12 x 12 = 144 = 1 grosse Mesure 1 pied = 12 pouces 1 pouce = 12 points Monnaies Charlemagne (vers 800) 1 livre (libra) = 20 solidi (sous, sols ou schillings) 1 solidi = 12 denarii (deniers ou
pfennigs). Monnaies britannique (jusqu'en 1971) 1 livre = 20 shillings 1 shilling = 12 pence. |
|||
|
Pour en savoir plus |
>>>
Nombre 12 >>>
Douzaine et base 12 >>>
Bases de numération |
>>>
Jeux avec 12 >>>
Divisibilité par 12 >>>
Horloges |
||
183.
Nombres de Mersenne – 2n – 1
|
|
|||
|
Définition Un
nombre de Mersenne est tout simplement une puissance de 2 moins 1. Mersenne et Parfait Lorsque
le nombre de Mersenne est premier, il est la source d'un nombre parfait: 2n – 1 x (2n – 1) Théorèmes Si un nombre de Mersenne est
premier, alors n est premier. La réciproque n'est pas vraie. Si a et n sont deux entiers
(>1) et si an – 1 est premier alors a = 2 et n est premier. |
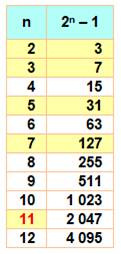
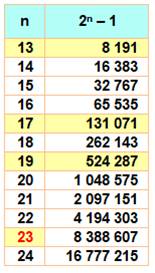
Liste pour les premières valeurs
Mersenne premiers En
jaune les nombres premiers. Tous
les nombres de Mersenne premier sont formés avec n premier. Un
nombre n premier n'engendre pas automatiquement un Mersenne premier (cas de
11 ou 23). |
|||
|
Brèves associées |
>>>
Nombres parfaits |
|||
|
Pour en savoir plus |
>>>
Nombres de Mersenne >>>
Marin Mersenne (1588-1648) |
>>>
Nombres premiers |
||
184.
Nombre 10 – DIX
|
|
|||
|
Linguistique Déca
veut dire 10 fois plus et déci 10 fois moins. Une
décade vaut 10 jours et une décennie 10 ans. Attention: decade en anglais =
10 ans. Le
décan vaut 10 jours en astrologie. Décimer:
diviser par dix. Tuer neuf personnes sur dix. Propriétés
Il
est triangulaire et tétraédrique. Curiosité:
10 décimal = 1010 binaire (10 répété!). En
chiffres romains, 10 est noté X. Mais, DIX romain vaut 500 + 9 = 509 en
décimal. Multiplication et division par 10 Il
suffit d'ajouter un 0 ou de décaler la virgule d'un cran vers la droite. Pour
diviser par 10, on fait l'inverse. |
Deux mains = dix doigts
Base de la numération décimale En
écrivant 234 on sous-entend: 2 centaines + 2 dizaines + 4, soit: 2 x 100 + 3 x 10
+ 4. Chaque
chiffre a un poids dix fois plus grand que son voisin juste à droite. C'est
la position qui compte; et, comme il y a dix chiffres, on dit que nous
comptons avec un système de numération décimale de position. Curiosités
210
= 1024 J'ai dix ans Dix
ans correspondent à une vie de plus de 315 millions de secondes. |
|||
|
Brèves associées |
>>>
Nombre 9 >>>
Compter avec 10 chiffres |
>>>
Nombre 11 |
||
|
Pour en savoir plus |
>>>
Nombre 10 – Culture >>>
Nombre 10 – Maths >>>
Chiffre romains |
>>>
Main >>>
Système décimal >>>
Pépites numériques |
||
185.
Nombres complexes
|
|
|||
|
Démystification! On
n'aurait pu (dû) les appeler les nombres doubles, ou doublon. En effet, il
s'agit de créer une algèbre sur des couples de
nombres. On
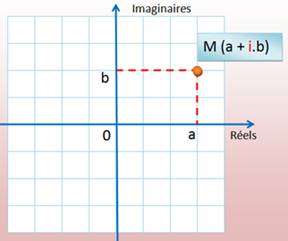
note le couple: a + i . b Note:
Il existe des quadruplets: les quaternions. Que représente le nombre i ? Le
nombre i est une création particulièrement astucieuse. Il représente aussi
bien:
Autrement
dit, le premier nombre représente un point sur la droite classique
horizontale et le second un point sur une droite verticale. Un nombre
complexe définit, tout simplement, les coordonnées d'un point M du plan. Intérêt En
introduisant des nombres imaginaires dont les carrés sont négatifs, toutes
les équations du second degré ont une solution avec deux racines,
éventuellement complexes. Exemples
|
Définition
Représentation
Applications D'une
manière générale, les complexes font partie de la boîte à outils des
ingénieurs. Les électroniciens les utilisent pour
décrire le comportement des circuits électroniques en régime permanent comme
en régime transitoire. |
|||
|
Pour en savoir plus |
>>>
Nombres complexes >>>
Équations du second degré |
>>>
Coordonnées >>>
Électronique |
||
186.
Carré = cube
|
|
|||
|
Question Est-ce
qu'il existe beaucoup de nombres égaux à la racine carrée d'un cube?
Ou,
exprimé d'une autre façon (en élevant au carré):
Réponse Oui!
Il suffit que N soit lui-même un cube.
Alors
K sera évidemment un carré:
Exemples
|
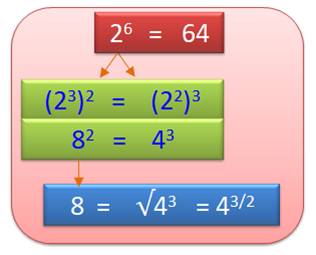
Carré x cube = puissance 6 On
retrouve la propriété énoncée en partant d'une puissance sixième. Celle-ci
est à la fois le carré d'un cube et le cube d'un carré.
Le
nombre 8 est égal à la racine carrée d'un nombre cube (64 = 43). Notez
la notation fractionnaire: le 2 au dénominateur veut dire racine carrée |
|||
|
Brèves associées |
>>> Carré
= somme de cubes |
|||
|
Pour en savoir plus |
>>>
Carré = cube >>>
Carrés >>>
Cubes |
>>>
Nombre 8 >>>
Racine carrée >>>
Puissance fractionnaire |
||
|
Programme (Maple)
|
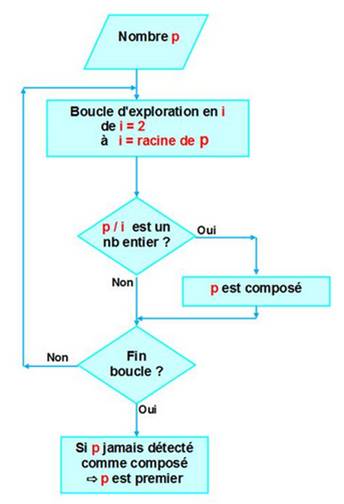
On
écrit un programme général, dit procédure,
qui teste si le nombre n est premier; puis un
programme principal qui produit la liste des nombres premiers. Le symbole #
indique que la ligne est un commentaire. La procédure TP sera exécutée
pour le nombre n. Initialisation
en déclarant que les variables i, imax et premier sont utilisées uniquement dans ce
programme. On
donne la valeur entière de la racine carrée de n
à imax et premier
est positionné à vrai. La
boucle pour i de 2 à
imax est lancée. Si on trouve que la partie fractionnaire (frac) de n/i est
nulle, c'est que la division est exacte, sans reste. Le nombre n n'est pas premier. Et, inutile de continuer la
recherche (i = imax). On
finalise en fermant la condition (fi), la
boucle (od), en retournant la valeur de premier, et en signifiant que la procédure est
terminée. Le programme principal déclare une liste P. On
analyse tous les nombre de 2 à 100 (valeurs
au choix) et, pour chacun, on teste si le nombre n
est premier en appelant la procédure TP. Si
le nombre est premier, il est ajouté à la liste P.
Cette instruction se lit: dans P on place une
liste [ ] qui contient la liste P connue op(P)
et le nombre n en plus. Le
programme terminé (od), on demande
l'affichage de la liste P. |
||
|
Brèves associées |
>>> Nombres
premiers >>>
Premiers en 6k+1 et 6k+5 |
>>> Infinité
de nombres premiers >>>
Premiers et cryptographie |
|
|
Pour en savoir plus |
>>> Crible
d'Ératosthène et sa programmation >>> Algorithme >>>
Le plus grand nombre premier connu |
||
188.
Polygones
|
|
|||
|
Polygone (poly = nombreux et gonos = angles) Figure géométrique du plan composée d'une
succession de segments formant une chaine fermée. Polygone régulier Ses côtés ont la même longueur (équilatéral) et
ses angles ont la même mesure (équiangle). Périmètre et aire De tous les polygones à n côtés, c'est le
polygone régulier à n côtés qui offre le maximum de surface. De tous les polygones à n côtés ayant une aire
donnée, c'est le polygone régulier à n côtés qui offre le périmètre minimum. |
Convexe Croisé Concave
Équilatéral Équiangle Régulier |
|||
|
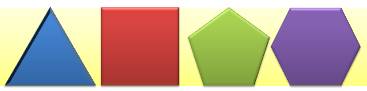
Polygones réguliers
Triangle
équilatéral / Carré / Pentagone / Hexagone / Heptagone / Octogone / Décagone
/ Dodécagone
Polygones étoilés |
||||
|
Brèves associées |
>>>
Triangles et polygones |
>>>
Brèves de géométrie – Index |
||
|
Pour en savoir plus |
>>>
Polygones – Index |
>>>
Hexagone >>>
Noms des polygones |
||
189.
Somme de consécutifs
|
|
|||
|
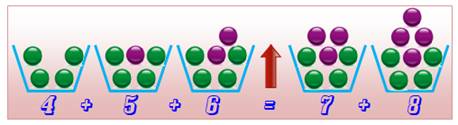
Énigme Combien
de billes dans chaque pot de manière à établir l'équilibre. Chaque
pot contient une bille de plus que le précédent. Quelques sommes
Avec
100, le carré de 10, il y a 10 nombres à droite et 11 à gauche, le premier à
gauche étant 100. |
Quantité de billes nécessaires pour l'équilibre
En
commençant par 5 billes ou plus, la balance penchera vers la gauche et cela
même en échangeant des nombres d'un plateau à l'autre. Comparez les écarts
entre quantité de billes vertes et de billes violettes. Théorème La somme de k + 1 nombres successifs à partir de k² est égale à la somme des k suivants. Exemple |
|||
|
Brèves associées |
>>> Somme:
1 + 2 + 3 + 4 + … |
>>> La
suite qui se lit |
||
|
Pour en savoir plus |
>>>
Énigme des cinq pots et sommes de consécutifs >>>
Nombres consécutifs – Index |
|||
190.
Pesée des neuf billes – Énigme
|
|
|||||
|
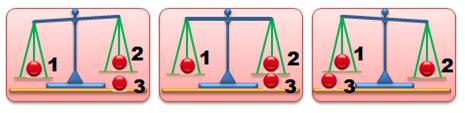
Parmi trois
billes visuellement identiques, une seule est légèrement plus lourde. La retrouver en une
seule pesée avec cette seule balance à plateau. |
Principe de pesée
|
|||||
|
Balle lourde |
Bille 1 |
Bille 3 |
Bille 2 |
|||
|
Parmi neuf
billes visuellement identiques, une seule est légèrement plus lourde. La retrouver en deux
pesées. |
Il suffit d'appliquer
le principe de pesée deux fois:
Notez que ce principe peut s'appliquer en cascade pour 27
billes en trois pesées ou 81 billes avec 4 pesées, etc. |
|||||
|
Brèves associées |
>>>
Poules et œufs >>> Énigme
des 30 euros |
>>>
Énigme de la pesée des quatre billes |
||||
|
Pour en savoir plus |
>>>
Énigme de la pesée des neuf billes >>>
Énigmes de pesées – Débutants et accès à tous les énigmes de pesées |
|||||
191.
Relativité
|
|
|||
|
Avec le son En
voiture à 80 km/h, la voiture devant moi qui roule à 110 km/h, s'éloigne de
moi à 30km/h. En
route à une vitesse égale à la moitié de celle du son (1 200 km/h), le son que
j'émets se propage devant moi à la moitié de sa vitesse normale. Dans
ce monde, tel que l'avait bien vu Galilée et que Newton a théorisé, les
vitesses objet-son se composent (s'ajoutent et se retranchent). Un
monde normal, quoi! |
Avec la lumière
Dans
ce monde à très grande vitesse, les vitesses objets-lumière ne se composent
pas. On parle de monde relativiste. En
1905, Einstein affirme: la vitesse de la lumière est une constante et rien ne
peut aller plus vite. |
|||
|
Masse Einstein,
via sa célèbre formule E = mc², indique
que l'énergie et la masse sont la même entité physique sous deux
formes différentes: l'une peut être changée en l'autre – Principe
d'équivalence. Masse en mouvement Un
objet en mouvement possède sa masse propre plus une masse due à l'énergie
cinétique (l'énergie du mouvement) Alors,
plus un objet va vite, plus il est "lourd".
|
Effet à très grande vitesse À
la vitesse de la lumière (ou presque):
|
|||
|
Brèves associées |
>>>
Formule de la relativité |
>>>
Brèves Sciences – Index |
||
|
Pour en savoir plus |
>>>
Relativité de Galilée >>>
Relativité d'Einstein >>>
Vitesse du son (330 m/s) >>>
Masse |
>>>
Galilée – Biographie >>>
Einstein – Biographie >>>
Célérité de la lumière (300 000 km/s) >>>
Spectre visible |
||
192.
Calculatrice
– Outils de calcul
|
|
|||
|
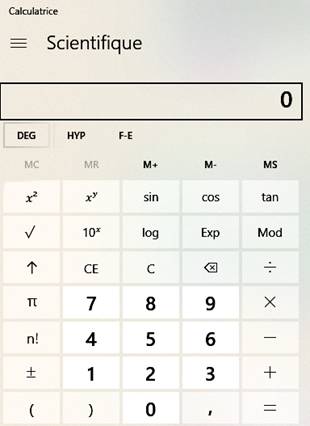
La calculatrice de votre ordinateur Elle
effectue tous les calculs en présentant un résultat sur 32 chiffres. Le
tableur Excel n'en offre que 15. Un logiciel de calcul (Maple ou Maxima) en
offre davantage. Accès à la calculatrice de votre ordinateur Taper
calculatrice dans la fenêtre en bas à gauche de l'écran.
Ou
alors, cliquez la fenêtre à quatre carreaux et chercher calculatrice parmi
les programmes listés. Petites choses à savoir Mette
la calculatrice en mode scientifique (cliquez en haut à gauche). Mettre
les angles en degrés ou radians en cliquant sur la touche DEG. La
touche |
|
|||
|
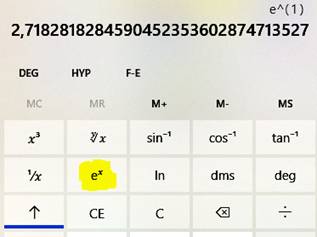
Extension des fonctions On
dispose de deux rangées de fonctions que l'on peut basculer pour obtenir
(généralement) les fonctions inverses. Cliquez sur la touche flèche ver les haut. Exponentielles L'exponentielle
est obtenue avec la touche ex et non pas la touche EXP (exposant)
qui permet de spécifier un exposant (une puissance) à un nombre. |
|
|||
|
Pour en savoir plus |
>>>
Calculatrice |
>>>
Tableur |
||
193.
Premiers résistants
|
|
|||
|
357 686 312 646 216 567 629 137 = 3,5… 1023 Ce
nombre premier de 24 chiffres est remarquable. Si on lui retire le dernier
chiffre à gauche, il est encore premier. En
fait, il reste premier à chaque fois qu'un chiffre à gauche est effacé. Il
existe exactement 260 nombres premiers résistants par la gauche et 83 par la
droite. Le
plus grand premier résistant à droite: 73 939 133. Il
existe 15 nombres qui sont résistants à la fois à droite et à gauche, dont le
plus grand: 739 397 |
Exemple de nombres premiers résistants par la gauche (à l'exception du 1 final, mais notable du fait
de la présence des 3) 33 333 331 3 333 331 333 331 33 331 3 331 331 31 |
|||
|
Brèves associées |
>>>
Premiers jumeaux |
>>>
Premiers en 6k+1 et 6k+5 |
||
|
Pour en savoir plus |
>>>
Premiers résistants |
>>>
Nombres premiers >>>
Nombre en 1023 |
||
194.
Suite de
carrés de nombres consécutifs
|
|
|||
|
Belle
suite d'égalités entre carrés de nombres consécutifs. Elle se prolonge à
l'infini. Le
nombre central (4, 12, 24 ou 40) est flanqué d'autant de termes de chaque
côté. Avec
k termes de part et d'autre du central, le nombre central est: |
Le triplet de Pythagore
le plus célèbre (3² + 4² = 5²), peut être prolongé indéfiniment par des
sommes du même type mais avec plus de termes.
|
|||
|
Brèves associées |
>>>
Pépites numériques |
>>> La
suite qui se lit |
||
|
Pour en savoir plus |
>>>
Suite de carrés de nombres consécutifs >>>
Triplets de Pythagore |
|||
195.
Triplets doublement carré
|
|
|||
|
a + b
= c² et a² + b² = d² Triplet
de Pythagore dont la somme des deux termes est aussi un carré. Le plus
petit cas et, en plus, c'est un double motif. Il existe
19 tels motifs pour a et b jusqu'à 1000. En majorité, ils sont doubles comme
pour 49. |
Plus petit exemple 9 + 40
= 7² =
49 9² + 40² = 41² = 1 681 Mise en évidence du double motif pour 49 49 = 7² = 9 + 40 et 9² + 40² = 41² = 1 681 49 = 7² = 21 + 28 et 21² + 28² = 35² = 1 225 |
|||
|
Brèves associées |
>>>
Triplets de Pythagore |
>>> Belle
égalité entre carré et cubes |
||
|
Pour en savoir plus |
>>>
Triplets doublement carrés |
>>>
Carrés des nombres |
||
196.
Somme des entiers – Démonstration
|
|
||
|
La formule donnant la somme des nombres
entiers de 1 à n est bien connue: S = ½ n (n + 1). Il est facile de calculer
la somme comme l'a fait le jeune Gauss. Mais comment démontrer cette formule?
Voici une méthode algébrique astucieuse utilisant un polynôme générateur. |
S = 1 + 2 + 3 + … + n On tente un polynôme générateur
en n², un de degré de plus que dans la somme. S = A + B.n + C.n² |
||
|
Pour n Pour (n + 1) |
Sn = 1 + 2 + … + n Sn+1 = 1 + 2 + … + n + (n+1) |
Sn = A + B.n +
C.n² Sn+1
= A + B(n+1) + C(n+1)² = A + B.n
+ B + C.n² + 2C.n + C |
|
|
Différence Comparaison |
D = n + 1 Coefficient de n: Partie constante: |
D
=Sn+1 – Sn = B + C + 2C.n 1
= 2C => C = 1/2 1
= B + C => B = 1/2 |
|
|
Remplacement |
Sn = A + Bn + Cn² |
Sn = A + ½ n + ½ n² |
|
|
Valeur de A |
Pour n = 1 => S1 = 1 |
S1 = A +
½ + ½
= 1 => A = 0 |
|
|
Formule finale |
|
|
|
|
Vérification |
S4 = 1 + 2 + 3 + 4
= 10 |
Sn
= ½ |
|
|
Brèves associées |
>>> Somme:
1 + 2 + 3 + 4 + … |
>>> Identités
1 + x + x² + … |
|
|
Pour en savoir plus |
>>>
Somme – Méthode de Gauss >>>
Somme de 1.2 + 2.3 + … – Même méthode pour des sommes de produits >>>
Somme des carrés, des cubes avec même méthode >>>
Polynôme |
||
197.
Recherche de facteurs
|
|
|||
|
Décomposition
en facteur premiers Recherche des divisibilités
ultimes des nombres. Les nombres atteints sont des nombres premiers et ceux qui constituent le produit
redonnnant le nombre sont les facteurs du
nombre. Par exemple:
100 est divisible par 2: 100 = 50 x 2 et 50; à son tour, 50 est divisible par
2: 50 = 25 x 2. Et, finalement 25 = 5 x 5. En résumé: 100 = 2 x 2 x 5 x 5 = 2² x
5² |
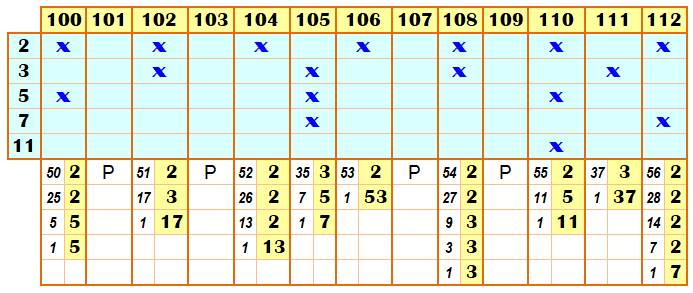
Procédé Pour une recherche
systématique, les nombres sont alignés. Une croix indique les nombres:
Ayant constaté ces
divisibilités, reste à effectuer les divisions successives (partie
inférieure du tableau). |
|||
|
Factorisation
des nombres de 100 à 112
Théorème
fondamental de l'arithmétique: il affirme que la décomposition en facteurs
premiers est unique sauf à échanger (permuter) les facteurs. Ex:
105 = 3 x 5 x 7 = 3 x 7 x 5 = 5 x 3 x 7 =
5 x 7 x 3 = 7 x 3 x 5 = 7 x 5 x 3. |
||||
|
Brèves associées |
>>> Cinq
nombres divisibles par 3 |
>>>
Diviseurs d'un nombre |
||
|
Pour en savoir plus |
>>>
Facteurs et diviseurs >>>
Th. fondamental de l'arithmétique |
>>>
Nombre 100 >>>
Critères de divisibilité |
||
198.
Carré
et cube à la fois
|
|
|||
|
Propriété Les nombres à la fois carrés
et cubes sont nécessairement des puissances sixièmes: 64 = 26 = 82
= 43 Or, avec le petit
théorème de Fermat
Valeur 0 pour n divisible par p et 1, sinon. Calculateur
prodige Question parfois posée:
trouver un nombre tel que la racine carrée est séparée de 18 de sa racine
cubique. Réponse: 729. |
Motif avec
racine carrée et racine cubique
Un nombre carré et cube à la fois (puissance 6e) est de la forme 7k ou 7k + 1. |
|||
|
Brèves associées |
>>>
Relation entre carrés et cubes |
>>> Unités
des puissances |
||
|
Pour en savoir plus |
>>> Carré et
cube à la fois |
>>>
Calculateur prodige Inaudi |
||
199.
Palindromes
|
|
|||
|
Motif palindrome Un
palindrome est un motif qui se lit de la même manière de gauche à droite ou
de droite à gauche, comme SOS, RADAR, EVE… Un
motif répété par un miroir peut être un palindrome. Mais ce n'est pas le cas
des mots ou des nombres pour lesquels chaque lettre ou chiffre est conservé à
l'endroit. RESSASSER
est le mot palindrome le plus long de la langue française. Humour Un
RADAR à double sens flash les automobilistes dans un sens ou dans l'autre. Au jardin d'Eden: – Madam I'm Adam – Eve! |
Nombres palindromes de divers types Un
nombre palindrome: 12344321 Une
addition palindrome: 38 + 83 = 121 Multiplication:
1 089 x 9 = 9 801 Palindrome
premier: 101 Palindrome
uniforme: 111, 666 Palindrome
triangulaire: 3003 Palindrome
carré: 101² = 10201 Palindrome
cube: 113 = 1331 Palindrome retard Somme
itérative avec le retourné: 69 + 96 = 165 + 561 = 729 + 627 = 1353 + 3531 =
4884 Le
nombre 196 est le plus petit dont on ne sait pas s'il finit en palindrome:
nombre de Lychel. |
|||
|
Brèves associées |
>>>
Pépites numériques |
>>>
Brèves – Motifs et formes – Index |
||
|
Pour en savoir plus |
>>> Palindromes numériques |
>>> Palindromes mots et textes |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()