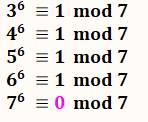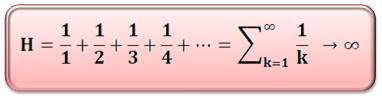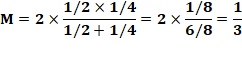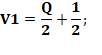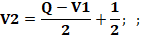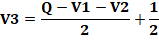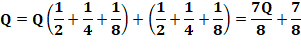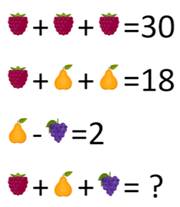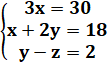NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Index général		Page 1 (1-19)		Page 2 (20-39)		Page 3 (40-59)		Page 4 (60-79)
	Page 5 (80-99)		Page 6 (100-119)		Page 7 (120-139)		Page 8 (140-159)		Page 9 (160-179)

BRÈVES de MATHS – Page 8

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

140. Factorisation
Factorisez		a² (b – c) + b² (c – a) + c² (a – b)
Développement		a²b – a²c + b²c – b²a + c²a – c²b
Mise en ordre		a²b – ab² – a²c – bc² + b²c + ac²
On ajoute abc et on le retranche		abc + a²b – ab² – a²c – bc² + b²c + ac² – abc
Factorisation en deux termes		a (bc + ab – b² – ac) – c (bc – b² – ac + ab)
Même facteur en commun		(a – c) (bc – b² – ac + ab)
Factorisation de la parenthèse		(a – c) (b – a) (c – b)
Pour en savoir plus	>>> Identités particulières		>>> Calcul avec parenthèses >>> Tracas classiques de calculs

141. Petit théorème de Fermat
Exemple de calcul avec 7 Prenons le produit de tous les nombres inférieurs à 7 : 1 x 2 x 3 x 4 x 5 x 6 = 6 ! En multipliant par 2 chaque nombre 2 x 4 x 6 x 8 x 10 x 12 = 2^6 x 6 ! En modulo 7 (reste de la division par 7) pour chaque chiffre 2 x 4 x 6 x 1 x 3 x 5 2^6 x 6 ! Ce produit est celui du début (pas dans le même ordre), alors, on remplace, toujours en modulo 7: 6 ! 2^6 x 6 ! On a la même chose en multipliant par 3: 3 x 6 x 2 x 5 x 1 x 4 3^6 x 6 ! Idem pour 4, 5 et 6. Mais, pas par 7 car alors 7^6 est divisible par 7.		Allons un peu plus loin Suite à cette petite manipulation astucieuse, on a donc : Dans factorielle 6, il n’y aucun diviseur de 7, on peut diviser par 6 ! Ce que l’on vérifié aisément : 64 = 6 x 7 + 1 Simple, certes ! Mais généralisable. Attention ça ne marche que pour des nombres tels que 7 et tous ses compagnons premiers.
Petit théorème de Fermat – Exemple 11^4 = 11^5 – 1 1 mod 5 14 641 = 2928 x 5 + 1		Théorème Pour tout nombre p premier. Valable tant que a n’est pas multiple de p.
Brèves associées	>>> Petit théorème – Théorie >>> Calcul modulo de 5^21 – 7^12		>>> Brèves Théorèmes – Index
Pour en savoir plus	>>> Petit théorème de Fermat >>> Calcul modulo		>>> Pierre de Fermat

Suite de la brève précédente

142. Nombre pseudo premier
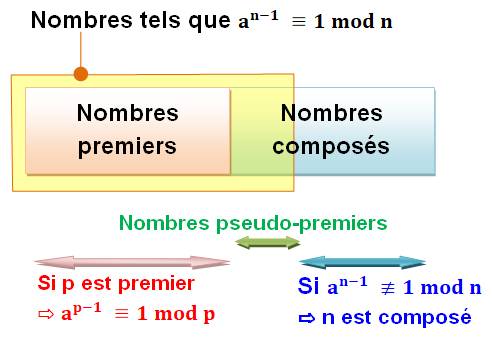
Le petit théorème de Fermat est vrai pour p premier. Très bien ! Mais, existe-t-il des nombres composés pour lesquelles cette relation est aussi vraie. Les Chinois pensaient que non (attesté vers 500 av J.-C.), à tort. Par contre, si la propriété de Fermat n'est pas vérifiée, le nombre p est composé.		En 1819, on découvre que 341, nombre composé est tel que : 2^340 – 1 est divisible par 341. Les nombres composés ayant cette propriété des nombres premiers sont appelés nombres pseudo-premiers. Même s’ils sont rares, il y en a une infinité. Jusqu’à 10^10, il y a 455 052 512 nombres premiers et 14 884 nombres pseudo-premiers. Le plus petit pseudo-premier pair est 161 038, découvert en 1950.
Brèves associées	>>> Nombres pseudo-premiers – Types
Pour en savoir plus	>>> Nombres premiers >>> Nombres composés		>>> Nombres pseudo-premiers >>> Nombres de Carmichaël

143. Orthographe des nombres
Règle La règle en vigueur depuis 1990 est résumée sur le tableau de droite. Avec le trait d'union systématique, on distingue désormais sans ambiguïté: soixante et un tiers (60 + 1/3) et soixante-et-un tiers (6 1/3). Exemples
Pour en savoir plus	>>> Nombres en toutes lettres >>> Orthographe des collectifs >>> Orthographe – Index		>>> Nombres par ordre alphabétique >>> Langue et linguistique – Index

144. Nombre 8 – HUIT
Infini En me couchant, je glisse jusqu'à l'infini Propriétés Nombre pair, cube de 2: 8 = 2 x 2 x 2 = 2^3 Aussi somme de deux carrés: 8 = 2² + 2² Les nombres 8 = 2^3 et 9 = 3^2 sont les deux seules puissances de nombres consécutifs. Le carré d'un nombre impair, diminué de 1, est divisible par 8: 11² – 1 = 121 – 1 = 120 = 8 x 15 Curiosités numériques 8 = 5 + 1 + 2 et 512 = 8^3. 1000 = 888 + 88 + 8 + 8 + 8 Découpe du gâteau en 8 Il suffit de trois coups de couteau: deux selon des diamètres et un horizontal découpant deux disques.		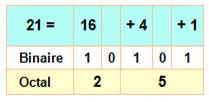Musique La gamme comporte huit notes: do, ré, mi, fa, sol, la, si, do ou C, D, E, F, G, A, B, C chez les anglo-saxons. Informatique Un octet est un regroupement de 8 bits (byte en anglais). On compte en octal en désignant trois bits par un chiffre. Alors, huit chiffres suffisent. Géométrie Une figure (polygone) à huit côtés est un octogone. C'est la forme du panneau routier STOP. il est facile à dessiner en traçant un cercle, le carré inscrit et les deux diagonales.
Brèves associées	>>> Nombre 7 >>> Binaire		>>> Nombre 9
Pour en savoir plus	>>> Nombre 8 – Culture >>> Nombre 8 – Maths >>> infini – Symbole		>>> Octogone >>> Jeux des huit 8. >>> Notes de musique

145. Plus grand nombre avec 3 chiffres
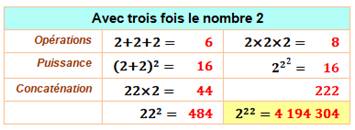
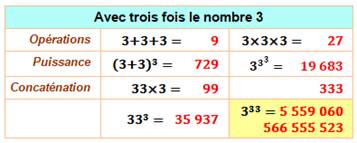
Trois chiffres 2 Savez-vous quel est le plus grand nombre qu'il est possible d'écrire avec trois fois le chiffre 2? On peut écrire 222, mais ce n'est pas le plus grand nombre. Avec un 2 porté à la puissance 22 (le nombre 2 multiplié vingt-deux fois par lui-même), on obtient un nombre qui dépasse les quatre millions: quatre-millions cent-quatre-vingt-quatorze-mille trois-cent-quatre.		Trois chiffres 3 On peut écrire 333, mais ce n'est pas le plus grand nombre. Comme avec 2, le plus grand nombre est 3 puissance 33 = 5,5… x 10^15 = cinq-mille-cinq-cent-cinquante-neuf-billions soixante-milliards cinq-cent-soixante-six-millions cinq-cent-cinquante-cinq-mille cinq-cent-vingt-trois.
Trois chiffres 9 On peut écrire 999, bien sûr, dépassé par 9^99 qui est un très grand nombre, voisin de 10^95 (un 1 suivi de 95 zéros). Mais, cette fois, il est possible de faire mieux avec 9 à une puissance égale à 9 à la puissance 9. On écrit (maths ou linéaire): Ce nombre comporte 369 693 100 chiffres.		Toujours plus grand L'introduction de l'opérateur factorielle est un moyen de faire exploser le compteur! Car 9! = 1x2x3x4x5x6x7x8x9 = 51 840. Notre plus grand nombre flanqué de factorielle devient: Un nombre avec plus de 10^2 millions de chiffres. Les mathématiciens ont inventé des notations sophistiquées pour désigner de tels nombres géants.
Brèves associées	>>> 10 en chiffres		>>> Factorielle
Pour en savoir plus	>>> Jeu des trois chiffres >>> Nombres en toutes lettres		>>> Nom des grands nombres >>> Notation des très grands nombres

146. Angles

Unités

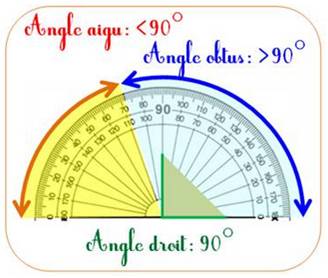
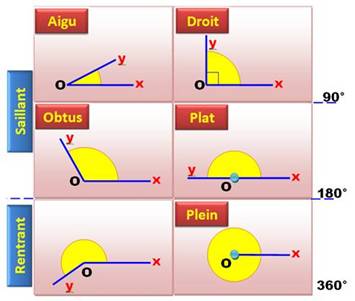
Types

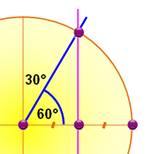
L'angle droit mesure 90°. Plus petit, l'angle est aigu et plus grand, il est obtus.

Bissectrice

La bissectrice est la demi-droite qui partage un angle en deux angles égaux.

Astuce de construction – Angle de 60°

La médiatrice d'un rayon coupe le cercle. Le rayon issu de cette intersection forme un angle de 60° avec le rayon initial.

Brèves associées

>>> Cercles et angles

>>> Cercle et Pi

Pour en savoir plus

>>> Angles – Index

>>> Bissectrice

>>> Médiatrice

147. Nombres géométriques
Nombres figurés/ géométriques / polygonaux Nombres formant des figures géométriques Depuis l'Antiquité, les hommes ont été séduits par les figures géométriques. Il s'agissait de créer des dessins plus faciles à retenir ou à manipuler. Ce fut le cas pour les étoiles dans le ciel avec le dessin des constellations. 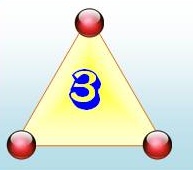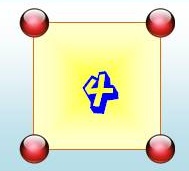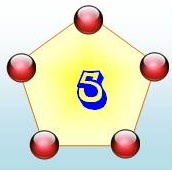Les mathématiciens de cette époque firent de même avec les nombres, en les arrangeant selon les figures géométriques les plus simples qu'ils connaissaient: le triangle, le carré, le pentagone, etc. les polygones. Exemple des nombres carrés 1, 4, 9, 16, 25 … La figure montre leur formation à partir du précédent et, en remontant, la formation des carrés comme somme des nombres impairs: 5² = 25 = 1 + 3 + 5 + 7 + 9			Le nombre 3 est triangulaire. Le nombre 4 est carré. Le nombre 5 est pentagonal.
Brèves associées	>>> Nombre triangulaires	>>> Théorie des nombres
Pour en savoir plus	>>> Nombres géométriques >>> Construction	>>> Nombres carrés – Index >>> Polygones – Index

148. Ensembles des nombres
Nombres entiers N: 1, 2, 3 … Ce sont les nombres ordinaires, ceux utilisés pour compter; des nombres ronds et positifs. Avec l'addition, la somme reste dans le monde des nombres entiers. Par contre, avec la soustraction, on peut obtenir des nombres négatifs. Nombres relatifs Z: …, -2, -3, 0, 1, 2, 3… Les nombres entiers accompagnés d'un signe plus ou d'un signe moins. Avec l'addition, la soustraction et la multiplication, le résultat est bien un nombre relatif. Par contre, avec la division, on peut obtenir des fractions qui ne se simplifient pas. Nombre rationnels Q: 1/2, -3/4, 1, 2 … Les fractions sont ajoutées. Cette fois les quatre opérations peuvent être effectuées et le résultat reste dans le monde des rationnels. Mais il existe des nombres qui ne sont pas des fractions, comme racine de 2. Nombre réels R comme Ce sont les nombres avec des chiffres derrière la virgule qui ne se répètent jamais. Certains ne sont même pas exprimables sous forme algébrique (polynôme); ce sont les transcendants, comme .		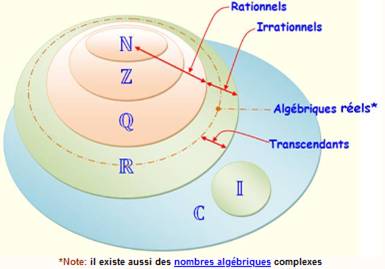Emboitement des ensembles de nombres Nombres complexes C: a + ib Une invention bien pratique qui consiste à associer les nombres par paires et à introduire un nombre imaginaire i tel que i² = -1. Cet artifice permet de résoudre une grande quantité d'équations et de problème de toutes sortes en maths comme en physique. Quaternions Sorte de nombres complexes à quatre composantes. Les octavions en ont huit. Ils sont utilisés en mécanique quantique, par exemple.
Brèves associées	>>> Théorie des nombres		>>> Diviseurs
Pour en savoir plus	>>> Ensembles des nombres >>> Noms des nombres – Index		>>> Les quatre opérations >>> Mécanique quantique

149. Somme des inverses des nombres
Série harmonique La somme des inverses des nombres entiers naturels, que l'on appelle aussi série harmonique, grossit de plus en plus pour atteindre l'infini. C'est Nicole Oresme qui le prouve au XIV^e siècle. Croissance Oui, elle diverge, mais très lentement: H = 2, 9289… pour 10 termes H = 5,1873… pour 100 termes H = 7,4854… pour 1000 termes H = 14,3927… pour un million de termes Harmonique Le nom fait allusion aux harmoniques en musique. Ils sont obtenus pour des fractions 1/2, 1/3 … de la fréquence fondamentale.		La série harmonique diverge Construction On ajoute indéfiniment les fractions égyptiennes successives (numérateur toujours à un). Moyenne harmonique entre 1/2 et 1/4 Chaque terme de la série est la moyenne harmonique de ses deux voisins. Paradoxe Un ver progresse sur une bande de caoutchouc qui s'étire en même temps. Est-ce que le ver arrivera au bout? Paradoxalement, jamais!
Brèves associées	>>> Somme des inverses des carrés		>>> Suite qui se lit
Pour en savoir plus	>>> Somme des inverses des nombres >>> Paradoxe du ver >>> Paradoxe des dominos empilés		>>> Fractions égyptiennes >>> Moyenne harmonique >>> Musique

150. La vente des œufs – Énigme
Énigme La fermière vend la moitié de ses œufs et un demi-œuf. Puis la moitié de ce qui reste et un demi. Et encore la moitié et un demi. Elle a tout vendu sans casser d'œuf. Combien d'œufs dans son panier en arrivant au marché? Indice Mettre sous forme de relation la vente de chaque jour et prendre en compte que la somme des ventes est égale à la quantité d'œufs au départ.		Solution Q = V1 + V2 + V3 Somme des trois ventes Q = 7
Brèves associées	>>> Chapeaux – Énigme		>>> Lapins et canards
Pour en savoir plus	>>> Énigmes classiques		>>> Jeux et énigmes – Index

151. Magie de la preuve par 9
Si on soustrait ses chiffres à un nombre, le résultat est toujours divisible par 9. Tour de magie: prends ton âge. Soustrais les chiffres. Le résultat est 9 ou un multiple de 9 (ou 0, si tu as moins de 10 ans). Ex: 17 ans: 17 – 1 – 7 = 9. 23 ans: 23 – 2 – 3 = 18.		Un nombre moins ses chiffres = 9k
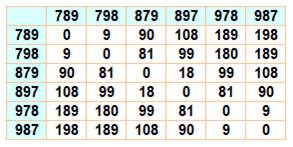
Si on soustrait un nombre et une de ses permutations de chiffres, la différence est divisible par 9. Rappel: un nombre est divisible par 9 si la somme de ses chiffres est aussi divisible par 9. Ex: 198 => 1 + 9 + 8 = 18 => divisible par 9.		Table de soustraction de ces nombres permutés (sans le signe)
Brèves associées	>>> Âge répété – Magie >>> Procédé de Kaprekar		>>> Divisibilité
Pour en savoir plus	>>> Preuve par neuf >>> Preuve par neuf en pratique		>>> Divisibilité par 9 >>> Formes permutées

152. Aire des parallélogrammes
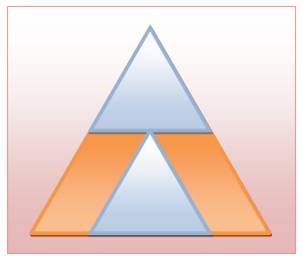
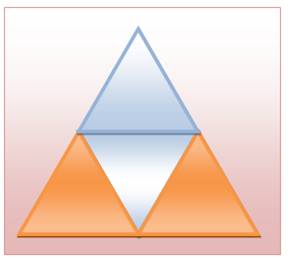
Énigme Un grand triangle équilatéral et deux petits identiques disposés l'un sous l'autre. Que peut-on dire de l'aire des deux parallélogrammes marron? Solution en image Il suffit de retourner le petit triangle équilatéral du bas pour se rendre compte que chaque parallélogramme occupe la place d'un petit triangle équilatéral (1/4 de l'aire du grand). Sinon La hauteur du grand triangle est le double de celle du petit. Les côtés sont également dans un rapport 2. Les deux triangles bleus occupent la moitié de l'aire du grand. Reste une moitié pour les deux parallélogrammes identiques: soit 1/4 du grand pour chacun; la même aire que pour chaque petit triangle.
Brèves associées	>>> Les neuf points en un seul trait		>>> Triangles – Types
Pour en savoir plus	>>> Triangle équilatéral		>>> Aire

153. Divisibilité par 45 de aaaabbbb
Énigme Quelles sont les valeurs de a et b telles que N = aaaabbbb soit divisible par 45? Une des solutions Divisibilité par 11 Tous les nombres en aaaabbbb sont divisibles par 11. En effet: a+a+b+b = a+a+b+b.		Solution Notons que a et b sont des chiffres: a < 10 et b < 10. Si N est divisible par 45, il l'est par 5 et par 9. Divisible par 5, alors b = 0 ou 5. Divisible par 9, alors 4a + 4b = 9k. Si b = 0, alors 4a = 9k et a = 9 (a < 10) et N = 99990000. Si a = 0 et b = 0, alors N = 00000000, trivial Si a = 0 et b = 5, alors 4a + 4x5 = 9k ou 4 (p + 5) = 9k alors p + 5 = 9 et p = 4 N = 44445555 Notez que ces deux nombres étant également divisibles par 11, ils le sont par: 11 x 45 = 495.
Brèves associées	>>> Divisibilité de 123456789 – Critères >>> Nombres uniformes – Repunit >>> Divisibilité avec des factorielles
Pour en savoir plus	>>> Nombres en aaaabbbb (bi-uniformes) >>> Nombres à motif >>> Divisibilité – Critères >>> Divisibilité par 11		>>> Nombre 44445555 >>> Nombre 99990000

154. Volume de la pizza
Mémorisation amusante Volume du cylindre de rayon Z et de hauteur A Avec écriture amusante sur la figure. Écriture plus conventionnelle:
Brèves associées	>>> Constante PI et le cercle
Pour en savoir plus	>>> Cylindre et volume de la pizza >>> Découpe de la pizza		>>> Mnémotechnique

155. Quatre, dix, vingt, cent
Quels sont les nombres que l'on peut écrire avec ces quatre adjectifs numéraux: QUATRE DIX VINGT et CENT ?		4 – Quatre 10 – Dix 20 – Vingt 24 – Vingt-quatre 80 – Quatre-vingts 90 – Quatre-vingt-dix 100 – Cent 104 – Cent-quatre	110 – Cent-dix 120 – Cent-vingt 124 – Cent-vingt-quatre 180 – Cent-quatre-vingts 190 – Cent-quatre-vingt-dix 400 – Quatre-cents 410 – Quatre-cent-dix 420 – Quatre-cent-vingt
Brèves associées	>>> Compter avec dix chiffres >>> Opérations mystérieuses (vues sur le Net)
Pour en savoir plus	>>> Nombres quatre, dix, vingt et cent >>> Numération décimale			>>> Écriture des nombres

156. Initiation au système d'équations
But Jeu proposé aux élèves de CM2 pour les amener à concevoir les équations sans les nommer. Chaque fruit représente son prix chez l'épicier. Ainsi: acheter trois fraises coûtera 30 centimes. Énigme En l'occurrence cette énigme est simple: si 3 fraises valent 30, alors 1 fraise vaut 10. avec cette information, 2 poires valent 18 moins le prix de la fraise, soit 18 – 10 = 8. Une poire vaut la moitié, soit 8 / 2 = 4. Si, du prix de la poire on retire le prix du raisin, il reste 2. C'est que le raisin vaut 2 Solution Fraise = 10, poire = 4; raisin = 2 Somme demandée: 10 + 4 + 2 = 16.		École primaire Collège
Brèves associées	>>> Égalité conservée – Équations >>> Algèbre: ax + b (opérations à trous)
Pour en savoir plus	>>> Système d'équations		>>> Équations

157. Pièce qui roule
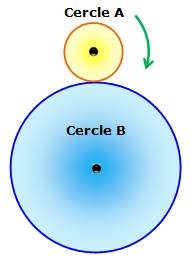
Énigme Deux cercles de rayon R et 3R. Le petit tourne sur le grand sans glissement. Après rotation, il retrouve sa position de départ. Combien de tours a-t-il effectué ? Indice Non ! ce n'est pas trois tours … C'est la réponse habituelle, mais elle est erronée. Solution Le cercle A effectue bien trois tours le long du chemin de roulement sur l'autre cercle (sur sa circonférence), mais en même temps, il tourne sur lui-même et effectue un tour supplémentaire. Engrenages Si les cercles étaient des engrenages montés sur des axes fixes, le petit pignon ferait trois tours pendant que le gros en exécuterait un de son côté. Un bilan de quatre tours.		Le cercle A roule sur le cercle B Pour revenir à sa position de départ, le cercle A effectue quatre tours.
Brèves associées	>>> Les chapeaux	>>> La chaine et ses maillons
Pour en savoir plus	>>> Énigme du cercle qui roule sur un autre >>> Jeux et énigmes – Index

158. Somme de chiffres identiques
Théorème pour nombres quelconques La différence entre deux nombres ayant la même somme de chiffres est divisible par 9. Exemples 18 – 9 = 9 40 – 31 = 9 75 – 48 = 27 = 9 x 3 Les nombres 75 et 48 ont la même somme de chiffres 12. Leur différence est divisible par 9. 222 – 51 = 171 = 9 x 19 987 654 – 456 789 = 530 865 = 9 x 58 985		Théorème pour nombres premiers La différence entre deux nombres premiers ayant la même somme de chiffres est un multiple de 2, de 3, de 6 et de 9. Exemples Somme 4: 13, 13 + 18 = 31, 31 + 72 = 103; Somme 5: 5, 5 + 18 = 23, 23 + 18 = 41; Les nombres premiers sont la somme des chiffres est 5 sont: 5, 23, 41, 113, 311, 401, 1013, 1031 … La différence entre eux est toujours un multiple de 2, 3, 6 et 9. Somme 6: aucun premier Somme 7: 7, 7 + 36 = 43, 43 + 18 = 61;
Brèves associées	>>> Critères de divisibilité		>>> Divisibilité du produit de nombres
Pour en savoir plus	>>> Somme de chiffres identiques et divisibilité par 9 >>> Chiffres des nombres premiers et multiples de 6

159. Énigme du parking
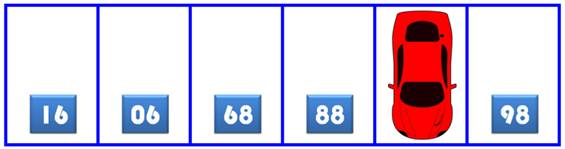
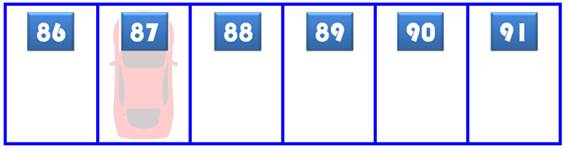
Quel est le numéro de la place de parking masqué par la voiture? L'astuce: en se plaçant de l'autre côté, on voit cette configuration: Note: Subtilement c'est le 87 qui a été caché par la voiture, car les nombres de 86 à 91 sont bien réversibles, sauf 87.
Brèves associées	>>> Opérations mystérieuses (vues sur le Net) >>> Année 2018 et ses chiffres
Pour en savoir plus	>>> Nombres retournés et leurs propriétés >>> Jeux et énigmes – Index

Retour	Brèves de maths – Page 7
Suite	Brèves de maths – Page 9
DicoNombre	Nombre 1 013
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve08.htm