NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Index général		Page 1 (1-19)		Page 2 (20-39)		Page 3 (40-59)		Page 4 (60-79)
	Page 5 (80-99)		Page 6 (100-119)		Page 7 (120-139)		Page 8 (140-159)		Page 9 (160-179)

BRÈVES de MATHS – Page 7

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

120. Nombre 6 et puissances
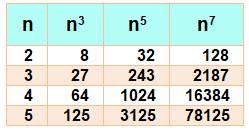
Pour toutes les puissances impaires Un nombre diffère de sa puissance impaire par un multiple de 6. Exemples 8 – 2 = 6 / 32 – 2 = 30 = 6 x 5 / 128 – 2 = 126 = 6 x 21 27 – 3 = 24 = 6 x 4 / 243 – 3 = 240 = 6 x 40 / Etc.		Avec de l'algèbre Calcul de la différence entre N^k – N en utilisant une identité remarquable pour les puissances impaires: n^k – n = n (n^k – 1 – 1) = (n – 1) n (n + 1) . M La différence est divisible par le produit de trois nombres consécutifs. L'un d'eux, au moins, est pair et, aussi, l'un d'eux est divisible par 3. La différence est bien divisible par 2 x 3 = 6. Exemples de factorisations n^3 – n = (n – 1) n (n + 1) n^5 – n = (n – 1) n (n + 1) (n² + 1)
Brèves associées	>>> Puissance – Introduction >>> Nombre 6		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres pairs et nombres impairs >>> Puissance des nombres		>>> Développement de n^k – n >>> Identités remarquables >>> Divisibilité de produits

121. Problème P = NP
Les problèmes simples ou P Lorsqu'il est possible de trouver une solution directement ou par exploration par ordinateur, on dit que le problème est simple ou plus précisément de type P (comme polynomial). Les problèmes compliqués ou NP Si la résolution est infaisable avec les ordinateurs même les plus puissants, on dit que le problème est NP. Il existe cependant de nombreux cas où, connaissant la solution, il est facile de vérifier que la solution est exacte. Le voyageur de commerce Établir le plan de visite d'un représentant est un problème NP. Comment trouver le parcours idéal pour passer partout avec le minimum de distance?		Comment les mathématiciens tentent de résoudre les problèmes NP: Par essais successifs de solutions; Par introduction d'une astuce; Par approximation; Par simulation simplifiée du problème; Etc. Le problème P = NP Une question qui interroge beaucoup de mathématiciens: Est-il possible de trouver une manière de ramener tous les problèmes NP à des cas P ou non? Voire, est-il vraiment possible de le démontrer ou, est-ce indécidable?
Pour en savoir plus	>>> Logique >>> problème P = NP		>>> Le voyageur de commerce >>> Ordinateurs les plus puissants

122. Le piège du nénuphar
Devinette Un nénuphar couvre un étang en 100 jours. Il double sa surface tous les jours. Quand avait-il couvert la moitié de l'étang ? Solution Bravo! Vous ne vous être pas laissé avoir. Ce n'est pas 100 / 2 = 50 jours pour recouvrir tout l'étang. Mais seulement un jour. Car, si la veille il couvre la moitié de la surface, le lendemain, ayant doublé de surface, il couvrira l'intégrité de l'étang.		Un peu d'anglais There is a pond and at the center of it grows a beautiful lotus flower. The size of the lotus keeps on growing double each day. If you look after twenty days, the lotus will have covered the entire pond. How much time will the lotus take to cover half of the pond? Vocabulaire Pond: étang / size: taille / To grow: pousser / to keep on: continuer / to cover: recouvrir To double: doubler / twenty: vingt / half: moitié.
Pour en savoir plus	>>> Paradoxe du nénuphar et exponentielles >>> La grenouille et les nénuphars >>> La nature et les nombres		>>> Double >>> Moitié >>> Bagage minimum en anglais

123. Un quatrillion (ex quadrillion)
Sable On estime que sur la Terre, il y a: 10^24 grains de sable 1 quatrillion de grains Le sable est formé de dioxyde de silicium, composante la plus abondante de la croûte terrestre avec une proportion de 42, 86 % en poids, soit 1,187 10^22 kg. Quatrillion Ce nombre quatre "fois" le million. En fait, c'est plutôt le million puissance quatre. (1 000 000)^4 = (10^6)^4 = 10^24 = 1 000 000 000 000 000 000 000 000 (un million de milliards de milliards)		Archimède (de 287 à 221 avant J.-C.) Archimède dans son ouvrage l'Arénaire a estimé la quantité de sable dans l'Univers à 10^63 grains. Dans son vocabulaire: 1000 unités du septième ordre de nombres. Il avait estimé la taille de l'Univers à 10^14 ce qui correspond à environ 2 années-lumière. C'est très petit par rapport à notre connaissance actuelle de L'Univers. Il faut deux fois plus (4 années-lumière) pour atteindre l'étoile la plus proche. Mais c'est une taille extraordinaire pour les connaissances de son époque.
Pour en savoir plus	>>> Étoiles dans l'univers >>> Quadrillion >>> Croûte terrestre >>> Pas dans le sable		>>> Archimède >>> Année-lumière >>> Univers >>> Terre

124. Théorème de Wilson
Intérêt Ce théorème aurait pu être intéressant car il offre la possibilité d'un test de primalité (reconnaitre les nombres premiers). Mais, mettant en jeu des factorielles, donc des nombres très grands, son intérêt est vite limité. Historique Sir John Wilson est un juge anglais qui se trouvait connaitre cette propriété et en parla à un professeur de mathématique de Cambridge. Celui-ci publie le théorème en 1770 en l’attribuant à Wilson, et le nom est resté. Cette propriété était déjà connue du baron Gottfried Leibniz (philosophe et mathématicien allemand, 1646-1716) prés de cent ans avant cette anecdote. En 1771, Louis de Lagrange (1736-1813) est le premier à en donner une démonstration. De son côté Gauss en fit la démonstration avec les congruences en quelques minutes.		Autre expression (p – 1) ! + 1 est divisible par p si et seulement si p est premier. On a aussi (p – 1) ! + 1 est divisible par p² si et seulement si p est premier sauf dans de rares cas (5, 13, 563 jusqu’à 10^5)
Pour en savoir plus	>>> Factorielle >>> Théorème de Wilson >>> Nombres premiers		>>> Leibniz (1646-1716) >>> Lagrange ( 1736-1813) >>> Gauss (1777-1855)

125. Nombre 7 – SEPT
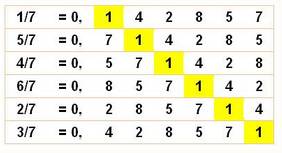
Propriétés Nombre impair et premier. En binaire 7 s'écrit 111. Division par 7 La division par 7 engendre un nombre périodique dont la période est: 7 – 1 = 6. 1 / 7 = 0,142857 142857… Selon le numérateur, les chiffres de la période sont décalés. Les sept jours de la semaine Une semaine compte 7 jours ou 168 heures ou 10 080 minutes ou 604 800 secondes.		Multiplication par 7 La table du 7 vous résiste! Observez le clavier numérique; il vous donne les unités des nombres à trouver. 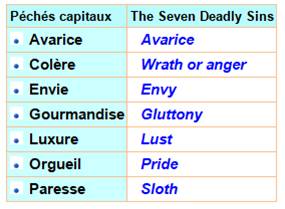Ex: 1 x 7 = 7; 2 x 7 = 14; 3 x 21; 4 x 7 = 28, etc. Les sept péchés capitaux
Brèves liées	>>> Nombre 6		>>> Nombre 8
Pour en savoir plus	>>> Nombre 7 – Culture >>> Nombre 7 – Maths >>> Multiplication par 7 – Finale		>>> Nombre périodiques >>> Semaine – Calcul du jour

126. Cubes et multiples de 9
Propriété exceptionnelle! La preuve par 9* d'un nombre au cube est toujours égale à 0, 1 ou 8. * Somme des chiffres, éventuellement répétée
Autrement-dit Un nombre divisé par 9 donne un reste égal à 0, 1 ou 8 Exemple 64 / 9 = 7 x 9 + 1			Ou encore Les cubes sont toujours un multiple de 9 ou voisin d'un multiple de 9. Exemple 126 = 14 x 9 125 = 5^3 = 126 – 1
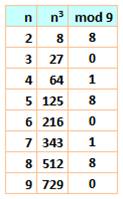
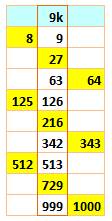
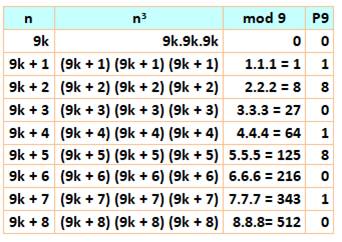
Pourquoi seulement ces trois valeurs? Un nombre quelconque, divisé par 9, donne un reste égal à 0, 1, 2, 3, 4, 5, 6, 7 ou 8. On peut le représenter sous la forme n = 9k + r avec r, un nombre de 0 à 8 (colonne de gauche). On calcule le cube de ces différents nombres (deuxième colonne). Dans le calcul de la preuve par neuf (ou en arithmétique modulo 9), tout ce qui est en 9 disparait. C'est le cas pour tous les 9k. Il suffit d'effectuer le produit de ce qui reste et de prendre la somme des chiffres type preuve par 9. La dernière colonne à droite montre bien la répétition du motif (0, 1, 8)			Table des cubes en mod9 Propriétés des sommes de cubes Somme de deux cubes divisée par 9: jamais 3, 4, 5, 6. Somme de trois cubes divisée par 9: jamais 4, 5.
Pour en savoir plus	>>> Cubes >>> Somme de trois cubes >>> Sommes de cubes			>>> Modulo >>> Preuve par 9 >>> Nombre 9

127. Énigme du Fortin
Le fortin bien gardé Un sergent place ses 36 gardes de sorte que chaque coté soit surveillé par 9 gardes. Les gardes sont malins. Comment font-ils pour obéir au sergent en effectif réduit?		L'astuce des gardes Effectivement, 18 gardes sont partis s'amuser et les 18 restants se sont placés sur les quatre tours des coins Avec une tour gardée par 4 gardes et sa voisine par 5 gardes, il y a bien 4 + 5 = 9 gardes par côté du fortin. La consigne du sergent est bien respectée.
Brèves liées	>>> Énigme des 30 euros		>>> Brèves Jeux – Index
Pour en savoir plus	>>> Énigmes – Index >>> Énigmes pour Juniors (diaporama)		>>> Nombre 36

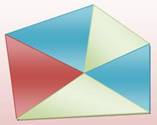
128. Octogone régulier
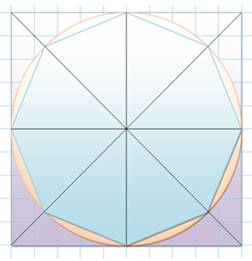
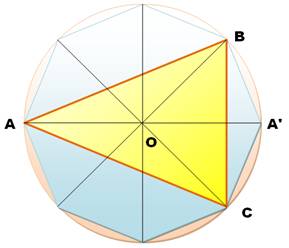
Composition L'octogone régulier est un polygone à huit côtés de même longueur. Il est formé de huit triangles isocèles (45° & 2x67,5°). Le triangle ABC est isocèle et semblable aux huit indiqués. Son angle en A vaut 45°. Le triangle ABA' est rectangle, car inscrit dans un demi-cercle. Son angle en B vaut 90°. Caractéristiques de l'octogone Utilisation Le panneau Stop est de forme octogonale. Sa forme est différente des autres pour le reconnaitre même si la neige en cache une partie.		Octogone, cercle et carré circonscrits Octogone et triangles
Brèves liées	>>> Hexagone		>>> Polygones et triangles
Pour en savoir plus	>>> Octogone >>> Polygones – Index		>>> Triangle isocèle >>> Nombre 8

129. Le X inconnu
Diophante, mathématicien du III^e siècle, nommait l'inconnue arithmos, le nombre. Al-Khawarizmi, au IX^e siècle, l'appelle SHAY, la chose. De AL-SHALAN, la chose inconnue. Les Andalous, alors sous influence arabe, transcrivent de mot en latin: XAY. Le SH pour le son CK n'existait pas. Le plus proche est le CHI latin, écrit X. On parle aussi de SHEI converti en XEI. Même origine que le CHOUÏA, connu en français.		René Descartes, au XVII^e siècle, n'aurait conservé que l'initiale X. En fait, nul ne sait d'où il tire cette lettre X. Ce dont on est sûr c'est qu'il est bien à l'origine de sa popularité. Il utilise les lettres minuscules du début de l'alphabet pour les quantités connues et celles de la fin pour les inconnues. Ces notations apparaissent dans ses manuscrits dès 1629. Il introduit également la notation des puissances comme x^3. Une histoire raconte que le linotypiste de Descartes lui aurait demandé de choisir x, car c'est une lettre peut employée, et donc plus disponible dans ses casiers de caractères. On pourrait aussi penser qu'il s'agit simplement du grec XENOS qui signifie inconnu. Il est tout à fait possible que Descartes ait fait lui-même un choix dans l'alphabet sans autre malice.
Brèves liées	>>> Orthographe des nombres		>>> Alphabet grec
Pour en savoir plus	>>> DicoMot-Maths – X >>> Langue – Index >>> Fréquence des lettres		>>> Diophante >>> Al-Khawarizmi >>> René Descartes

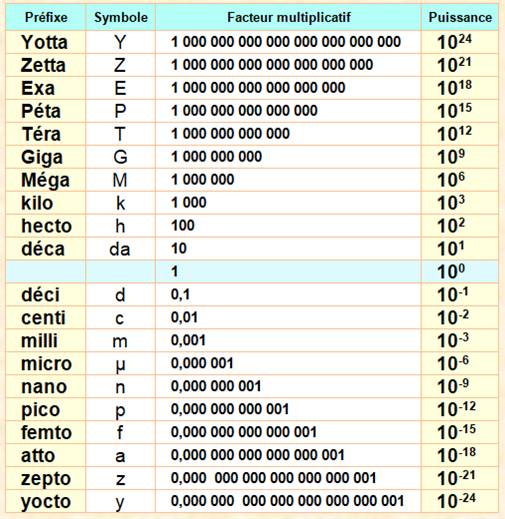
130. Préfixes multiplicateurs
Diviseurs déci divise par 10 – 1 dm = 0,1 mètre centi divise par 100 – 1 cm = 0,01 mètre milli divise par 1000 – 1 mm = 0,001 mètre micro divise par 1 000 000 – 1 µm = 0,000 001 mètre		Multiplicateur déca multiple par 10 – 1 dam = 10 mètres hecto multiplie par 100 – 1 hl = 100 litres kilo multiple par 1000 – 1 kg = 1000 grammes méga multiplie par 1 000 000 – 1 Mo = 1 million d'octets
Noms qui se terminent par i, puis par 0. Abréviations avec lettres minuscules, sauf micro (µ).		Noms qui se terminent par a, sauf hecto et kilo. Abréviations avec lettres majuscules, sauf kilo, hecto et déca.
Les 20 préfixes multiplicateurs officiels (système SI)
Pour en savoir plus	>>> Échelles de 10 >>> Notation ses petits et grands nombres		>>> Nombre 0,1 >>> Nombre 10

131. Théorie des nombres
Théorie des nombres En gros, la théorie des nombres c'est de l'arithmétique, mais généralisée. Plus précisément, c'est l'étude de l'ensemble des nombres entiers. Il existe toute une variété de familles de nombres entiers qui méritent que l'on s'intéresse à leurs propriétés propres. Types de familles de nombres (exemles)				Exemples de propriétés Tout nombre entier est décomposable de façon unique en produit de nombres premiers >>> Tout nombre entier est la somme de quatre carrés, au plus >>> Si p est un nombre premier, alors a et a^p ont le même reste lorsque divisés par p >>>
Famille		Exemple	Description				Lien
Entiers		0, 1, 2, 3 …	Les nombres habituels, utilisés pour compter.				>>>
Pairs		0, 2, 4, 6 …	Les nombres divisibles par 2.				>>>
Impairs		1, 3, 5, 7 …	Les nombres avec un reste de 1 lorsque divisés par 2.				>>>
1 mod 3		1, 4, 7, 10, 13, 16 …	Les nombres avec un reste de 1 lorsque divisés par 3.				>>>
Carrés		0, 1, 4, 9, 16 …	Égaux au produit de deux fois le même nombre.				>>>
Cubes		0, 1, 8, 27, 64 …	Égaux au produit de trois fois le même nombre.				>>>
Premiers		2, 3, 5, 7, 11, 17 …	Ils ne sont divisibles que par eux-mêmes ou par 1.				>>>
Composés		4, 6, 8, 9, 10, 12 …	Non premiers; produit de plusieurs nombres.				>>>
Fibonacci		1, 1, 2, 3, 5, 8, 13 …	Égaux à la somme des deux précédents (8 = 5 + 3).				>>>
Triangulaires		1, 3, 6, 10, 15, 21 …	Somme cumulée des entiers (10 = 1 + 2 + 3 + 4).				>>>
Parfaits		6, 28, 496 …	Nombre égal à la somme de ses diviseurs				>>>
Brèves associées	>>> Ensembles des nombres >>> Nombre 200 et théorie des nombres				>>> Brèves Nombres – Index
Pour en savoir plus	>>> Théorie des nombres				>>> Noms des nombres – Index

132. Majorant de 1/k²
Question Comment démontrer cette relation? Exemple Remarque Pour ne pas diviser par 0, il faut que k ne soit ni égal à 0, ni égal à 1; donc: k > 1. 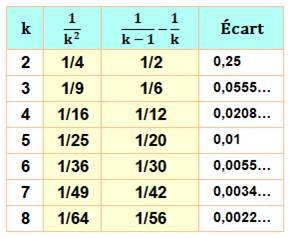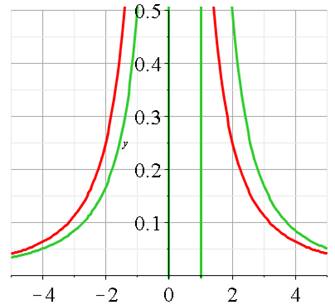Démonstration En réduisant au même dénominateur à droite: Si k > 1, le dénominateur k² – k = k(k – 1) est positif et plus grand que k; et l'inverse 1 / (k² – k) est plus petit que 1/k²: Si k < –1 , le dénominateur est positif et plus grand que k² et la relation est inversée: Valeur de la différence		Tableau de comparaisons Courbes de comparaison Pour les valeurs négatives de k, la courbe 1/k² (en rouge) est au-dessus de la verte (plus grand). Pour les valeurs positives de k, la courbe 1/k² est au-dessous de la verte (plus petit).
Brèves liées	>>> Parenthèses		>>> identité remarquables
Pour en savoir plus	>>> Fractions >>> Fractions égyptiennes		>>> Même dénominateur

133. Fibonacci – Programmation
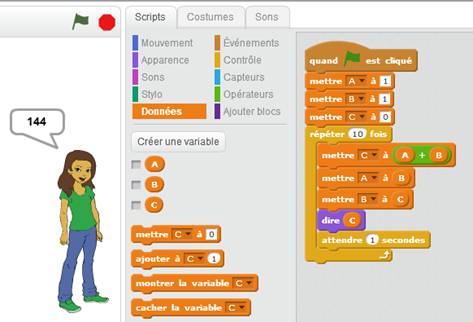
Suite de Fibonacci Chaque nombre est égal à la somme des deux précédents. Les deux premiers sont 1 et 1 et le suivant est donc: 1 + 1 = 2. Programmation Ci-contre, un exemple de réalisation avec Scratch. Trois variables A, B et C son créées. Elles représentent le nouveau nombre (C) et ses deux précédents (A et B). Une fois le calcul de C effectué, on met à jour les nouvelles valeurs de A et B, prêts pour le calcul suivant. Résultat Ce programme fait énoncer les nombres de Fibonacci par la jeune fille du 2^eau 12^e.		La scène / La palette de commandes / Le programme Après une répétition de 10 calculs au cours desquelles la jeune fille annonce les nombres successifs de Fibonacci, le programme s'arrête sur le 12^e nombre de Fibonacci: 144.
Brèves liées	>>> Suite de Fibonacci		>>> Premier programme (Scratch)
Pour en savoir plus	>>> Suite de Fibonacci		>>> Programmation – Index

134. Galileo & GPS
Galileo Galileo est le système GPS des Européens, lancé dans les années 1970 par la Commission européenne. Il est déployé depuis 2005 et il fonctionne avec 18 satellites en 2017. Actuellement, 42 pays participent au programme dont la Russie, les États-Unis et le Canada. Fonctionnement Les satellites diffusent leur identité et la valeur de leur horloge interne. Ces informations sont triangulées par nos récepteurs GPS à partir de quatre satellites. Leur position relative est connue en consultant des tables de référencement. Caractéristiques Précision de localisation: 1 et 4 m pour 5 à 10 m avec le GPS américain. Complément de positionnement disponible avec quelques dizaines de centimètres de précision. Service crypté de positionnement destiné aux administrations, résistant aux brouillages. Horloge Galileo: précision de 1 seconde en 3 millions d'années.		GPS: Global Positioning System Systèmes de GPS en service Applications (exemples) Les récepteurs sont de plus en plus multi-source et profitent des informations des différents systèmes de positionnement pour plus de fiabilité et de précision. Utilisation pour le système SAR (Search and Rescue – Recherche et Sauvetage). Pilotage automatique des véhicules. Transactions bancaires sécurisée par géolocalisation et clichés aériens au mètre près. Communications avec les objets connectés.
Brèves liées	>>> Points de Lagrange		>>> Brèves Sciences – Index
Pour en savoir plus	>>> Galileo >>> GPS		>>> Historique des GPS

135. Nombres narcissiques
Nombres narcissiques d'ordre 3 Nombres égaux à la somme des cubes de leurs chiffres. Ils sont 4 avec 370, 371 et 407. Avec la puissance quatre Ils sont 3 avec 8 208 et 9 474		Somme en puissance de 10 Tous les nombres avec ces chiffres, ou même des 0 en plus, donneront une somme égale à 100. Le nombre 112 est le plus petit de ce type avec une somme de 10 Cycle narcissique La somme des chiffres au cube est reconduite sur le nombre trouvé. 778 => 7^3 + 7^3 + 8^3 = 1 198 1 198 => 1^3 + 1^3 + 9^3 + 8^3 = 1 243 1 243 => 1^3 + 2^3 + 3^3 + 4^3 = 100 100 => 1^3 + 0^3 +0^3 = 1
Brèves liées	>>> Nombres carrés		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres narcissiques		>>> Cubes

136. Numéro de réservation
Totalisateur de kilomètres Il vous semble évident qu'avec ce compteur le maximum est 999 999 km, soit 1 000 000 de positions possibles en comptant de 000 000 à 999 999. Et, 1 000 000 = 10 x 10 x 10 x 10 x 10 x 10 = 10^6 Chaque molette peut prendre 10 positions. La première étant positionnée, la suivante peut prendre 10 positions. Soit 10 x 10 = 10^2 positions pour deux molettes. Avec k molettes, on aurait donc: 10^k positions possibles. Sans répétitions de chiffres Avec trois molettes, combien de nombres sans aucune répétition de chiffres ? La première molette étant positionnée, la suivante pourra occuper 9 positions, toutes sauf celle de la première. La troisième pourra occuper 8 positions, toutes sauf celles des deux premières. Soit 10 x 9 x 8 = 720 nombres sans répétition de chiffres.		Numéro de réservation Le même principe s'applique ici pour compter la quantité de possibilités de billets de réservation. Combien de positions sur chaque molette ? Les 26 lettres de l'alphabet et les 10 chiffres, soit 36 positions. La première molette étant positionnée, il y a 36 possibilités pour la suivante. Soit 36^6 = 2 176 782 336 numéros de réservation possibles. Suffisant pour recevoir un peu plus de deux milliards de passagers. Pas de doublons Si l'on veut éviter les doublons de lettres ou de chiffres, on décompte les possibilités comme vu ci-contre avec les trois molettes. Il y a 36 possibilités pour la première molette, puis 35 pour la suivante, etc. Soit 36 x 35 x 34 x 33 x 32 x 31 = 1 402 410 240 numéros de réservation sans lettres ou chiffres répétés.
Brèves liées	>>> Arrangements – Tiercé		>>> Puissance de 2 – Échiquier
Pour en savoir plus	>>> Dénombrements – Panorama >>> 2 milliards		>>> Chiffres >>> Lettres

137. Nombre 2 017
Écriture Français: Deux-mille-dix-sept Anglais: Two thousand seventeen Allemand: Zweitausend und siebzehn Premier Le nombre 2 017 est premier. Aucun nombre ne peut le diviser. Liste des 14 nombres premiers entre 2000 et 2100: 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099. Le nombre suivant est égal à deux fois un nombre premier: 2018 = 2 x 1009, un nombre presque-premier.		Somme de deux carrés Selon le théorème des deux carrés de Fermat: Tout nombre premier impair est la somme de deux carrés si et seulement s'il est de la forme 4n + 1. La somme des carrés est alors unique. Or, 2017 = 4 x 504 + 1 Et, effectivement: 2017 = 9^2 + 44^2 = 81 + 1 936 Autre forme amusante: 2017 = 3^4 + 2^4.11^2 Somme de quatre carrés Par contre, tout nombre est somme de quatre carrés, au plus. Par exemple: 2017 = 12² + 28² + 33² 2017 = 18² + 21² + 24² + 26²
Brèves liées	>>> Nombre 100		>>> Nombre 10
Pour en savoir plus	>>> Nombre 2017 >>> Nombres en lettres (orthographe)		>>> Somme de deux carrés >>> Somme de quatre carrés

138. Théorème des quatre couleurs
Historique Le problème des quatre couleurs remonte à une question posée en 1852, concernant la coloration des cartes représentant les comtés d'Angleterre. Il s'agissait de choisir une couleur pour chaque région sans frontière de même couleur, exception faite aux points de frontière entre plus de deux régions. Francis Guthrie est persuadé que quatre couleurs suffisent, d'autant que trois sont souvent suffisante. La preuve pour cinq couleurs est assez simple et elle a été publiée en 1890. Démonstration pour quatre couleurs En 1977, les mathématiciens arrivent à montrer que la propriété est pratiquement toujours vraie, sauf pour peu de cas particuliers. Il en reste tout de même de l'ordre de 1500. Impossible de les vérifier à la main. H. Heesh, K. Kapel et W. Haken écrivent un programme qui confirme que quatre couleurs suffisent pour ces cas pathologiques. En 2005, la vérification informatique est validée par Georges Gontier et Benjamin Werner à l'aide d'un logiciel assistant de preuve.		Cas classique à 3 et 4 couleurs Cas pathologique de Martin Gardner
Brèves liées	>>> Théorème de Fermat-Wiles		>>> Brèves Théorèmes – Index
Pour en savoir plus	>>> Théorème des quatre couleurs		>>> Graphes et quatre couleurs

139. Année 2018 et ses chiffres
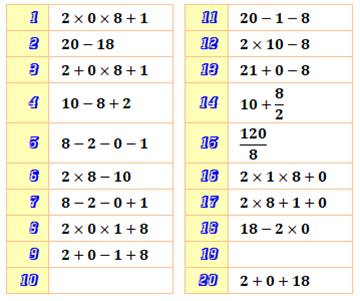
But En n'utilisant que les chiffres {2, 0, 1, 8}, une seule fois, former une opération dont le résultat est un nombre donné. Le but est de faire tous les nombres de 0 à n avec n le plus grand possible. Si possible en utilisant les chiffres dans l'ordre. Ce jeu peut même être proposé dès l'école primaire. Opérateurs autorisées Les quatre opérations; Les parenthèses; La concaténation (20, 18 …) L'élévation à une puissance, l'exposant étant un des chiffres; Les factorielles Défi Plus n est grand et plus le défi est grand et avec lui, la tentation de recourir à des fonctions arithmétiques avancées.		Saurez-vous trouver les manquants et prolonger la recherche ? Avec puissances: 10 = 2^0 + 1 + 8; 19 = 20 – 1^8 Une belle trouvaille pour les accros !
Brèves liées	>>> Dix en chiffres >>> Année 2016 – Minimale		>>> Nombres et ses chiffres
Pour en savoir plus	>>> Chiffres de l'année 2018 >>> Quatre opérations >>> Puissances		>>> Factorielles >>> Nombre 71 >>> Jeux de ce type – Index

Retour	Brèves de maths – Page 6
Suite	Brèves de maths – Page 8
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve07.htm