|
|||||||||||||||||||||||||||||
![]()
|
JEUX DIVERS avec DIX |
|
|
|
|
Problème
Variante
|
|
Voir Brève 54-1065
|
|
|
|
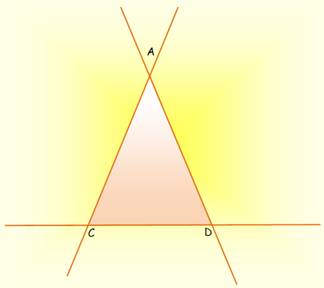
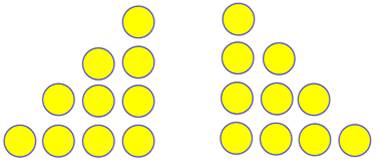
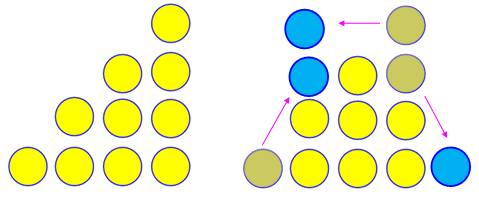
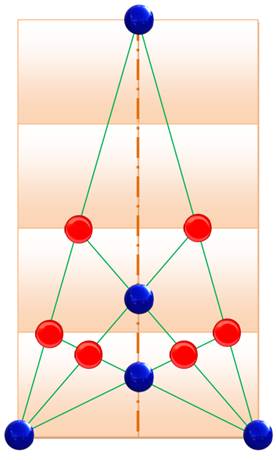
Problème Retourner la figure en déplaçant trois
pions.
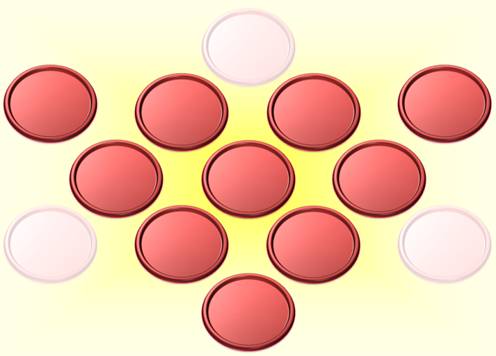
Problème
Variante du
solitaire Avec
la figure initiale, il est possible de
jouer au jeu du Solitaire. On retire une pièce. On prend une pièce en passant
par dessus, comme au jeu de dames. Il faut terminer avec un seul pion. |
|
|
|
||||||
|
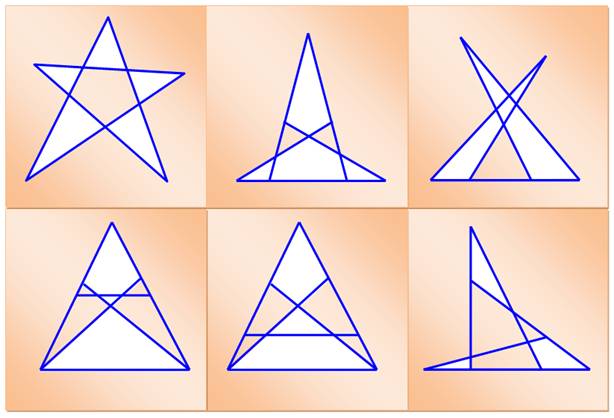
Caractérisation des énigmes
Problème 1
Problème 2
Problème 3
|
||||||
|
|
||
|
Dans le tiroir à chaussettes
|
Dans le tiroir à gants
|
|
|
|
|
|
Voir Somme de nombres divisibles
par 2 / Principe
des tiroirs
|
|
|
|
|
|
|
|
|
|
|
|
Voir Les 10 piles de 10 pièces / Énigme des 19 balles
|
|
|
|
|
|
![]()
Solutions
|
|
|
|
Solution
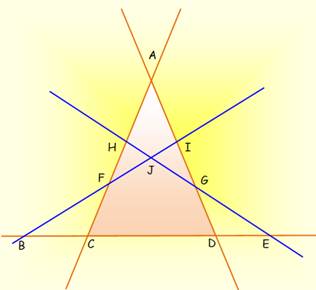
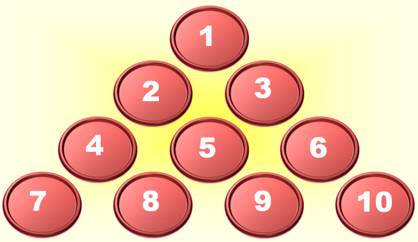
Nom des dix
triangles BCF, FHJ, GIJ, DEG BDI, CEH AIF, AGH ACD, BEJ |
|
|
|
|
|
Solution
Solution
Solution du
solitaire
On
retire le 6 1
10 – 3 2
1 –
6 3
8 –
10 – 3 4
4 –
6 – 1 – 4 5
7 –
2 |
|
|
|
|
|
Solution du 10 – 5 -
4 Il
y a six façons de résoudre ce problème.
|
|
|
Solution du 11 – 6 -
4
|
|
|
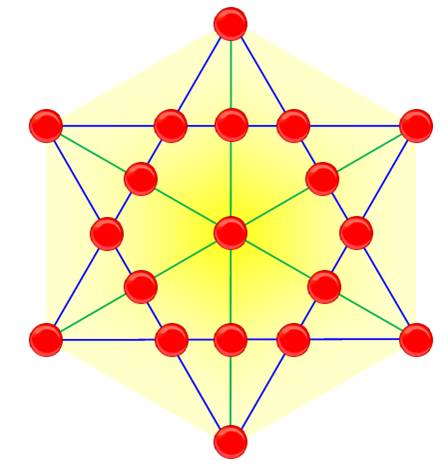
Solution du 19 – 9 -
5
|
|
Voir Étoile
mystique ou magique / Neuf points
/ Droite
|
|
||
|
Dans le tiroir à chaussettes
|
Dans le tiroir à gants
|
|
|
|
|
|
|
|
|
|
|
|
|
|
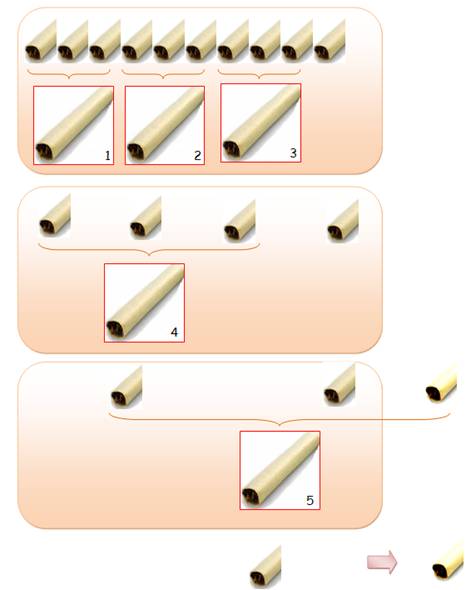
Illustration
|
|
|
|
|
|
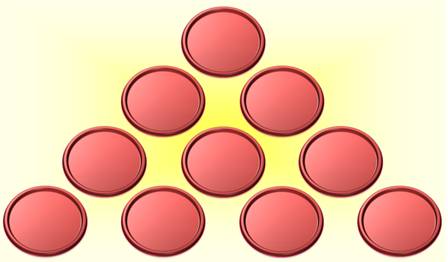
Ce qui donne: 1 + 2 + … + 10 = 10 x 11 / 2 = 55 pièces.
|
|
|
|
|
|
Solution Il pose la pièce sur un plateau et
toutes les autres sur l'autre plateau. Si la pièce choisie est normale, la
différence est égale à 6N + 5(N+1) – N = 10N + 5 Si la pièce choisie est plus lourde,
la différence est égale à 6N + 5(N+1) – (N+1) = 10N + 4 Il suffit de lire les graduations:
divisible par 5, alors la pièce est normale; si la pièce est plus lourde, la
graduation est paire. |
|
![]()
|
|
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()