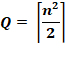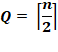|
Édition du: 28/03/2023 |
|
INDEX |
ÉCHECS |
||
|
Tournoi (organisation) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Tours indépendantes Comment placer
huit tours sur l'échiquier de façon qu'aucune ne soit en situation de prise
par une autre. Il s'agit du problème de l'indépendance
des tours comme il y a le problème bien connu de l'indépendance
des reines (ou dames). Le problème
s'applique généralement à l'échiquier classique 8x8. Il est souvent étendu à des
grilles carrées n·n ou même à des polyominos.
D'autres recherches concernent l'adjonction de pions. |
||
|
|
Sommaire de cette page >>> Périple de la tour >>> Calcul de chemins >>> Problème des quatre tours >>> Problème des huit tours – Approche >>> Solutions pour huit tours >>> Configurations
avec plus de tours >>> Graphe de déplacement des tours >>> Cas des sous-ensembles d'échiquier >>> Graphe de déplacement des tours – Théorie |
Débutants Glossaire |
|
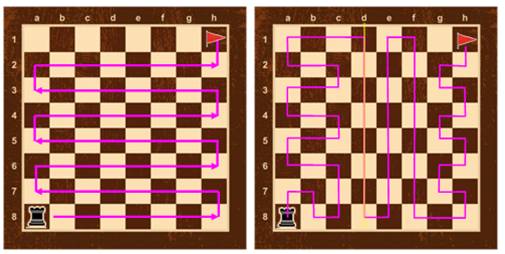
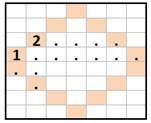
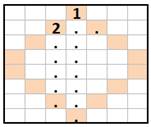
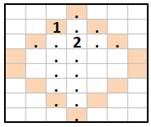
La tour doit parcourir toutes les cases en partant
du coin en bas à gauche pour arriver au coin en haut à droite. L'illustration montre deux parcours infructueux. Est-il possible d'y arriver ? Non ! Pourquoi ? Pour arriver au bout, il faut parcourir 63 cases,
un nombre impair. À chaque "pas" (passage d'une case à la
suivante), la case change de couleur.
Partant d'une case sombre, la 63e devra être claire. Or,
elle est sombre. Impossible ! |
Deux exemples La tour ne pourra jamais atteindre l'arrivée.
Commentaires Le périple n'est réalisable que pour un échiquier
à nombre impair de cases par côté. Le périple est réalisable sur l'échiquier
classique si on demande à la tour à revenir à son point de départ. Le
parcours le plus court comporte seize mouvements. |
|
Voir Chemin sur grille
type Manhattan / Pavage de l'échiquier
avec des dominos
|
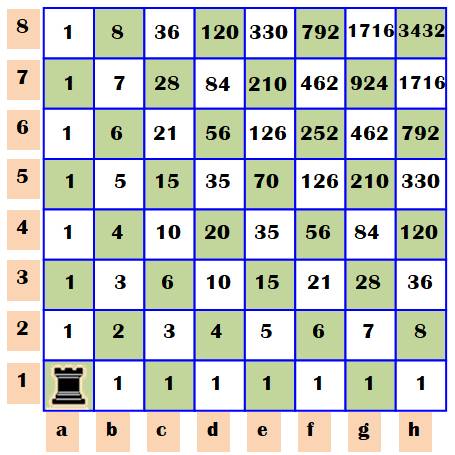
La tour doit atteindre la case h8 Elle peut prendre différents chemins. Combien ? Pour aller en b2, elle peut passer par a2 ou par
b1, soit deux chemins. On écrit 2 dans la case b2. Pour aller en c2, elle peut aller directement en
c1 (1 chemin) ou alors aller en b2 (2 chemins), soit 1 + 2 = 3 chemins. Etc. Chaque valeur est égale à la somme des valeurs
des cases à gauche et en bas. Pour arriver en h8, il y a 3 432 chemins. Le tableau est un sous-ensemble du triangle de
Pascal. Voir les diagonales descendantes. |
|
|
Voir Nombre
3 432 / Brève
47-936 / Voir Graphes
– Index
|
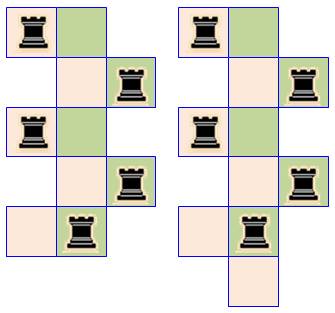
Placer quatre tours de sorte qu'elles maitrisent
toutes les cases blanches.. Quatre solutions: deux évidentes avec les
diagonales (en haut) et deux plus inventives (en bas). Les traits jaunes montrent les cases maitrisés
par le tours. |
|
|
|
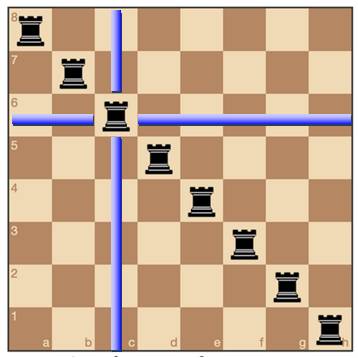
Selon les règles des échecs, la tour prend sur
les lignes horizontales et verticales comme le montrent les traits bleus sur
cet échiquier. La disposition présentée répond à l'exigence suivante:
aucune tour n'est menacée par une autre; autrement-dit: aucune tour ne se
trouve sur un trait bleu appartenant à une autre tour. On dit que les tours sont indépendantes (ou insaisissables). Nous tenons là une bonne solution. |
|
|
|
Méthode Pour trouver les solutions, il faut procéder méthodiquement:
Bilan: 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 8! = 40
320 Sur l'échiquier classique 8x8, il y a 40 320 solutions pour le problème des tours
indépendantes. Carré latin Les solutions correspondent à toutes les transversales
possibles du carré
latin; toutes les permutations
figurées de huit éléments. Remarque Toutes les tours sont interchangeables. Elles ne
sont pas identifiées. Sinon la quantité de dispositions serait bien plus
élevée. |
Une des nombreuses solutions
Pour trouver une solution, sur une ligne non
occupée, on place la tour sur une colonne non déjà occupée. On a ainsi, à la
fois, une tour sur chaque ligne et sur chaque colonne. |
|
Exemple de propriété cherchée
par les adeptes de ce genre de défi mathématqiue
|
Si on place quarante-et-une tours sur un échiquier normal, on peut
toujours trouver un ensemble de cinq tours indépendantes. |
|
Configurations avec PLUS de TOURS
en ajoutant un minimum de PIONS |
||
|
Le
problème des tours indépendantes passe pour être très simple. Un raffinement
consiste à ajouter un minimum de pions pour placer un maximum de tours
insaisissables |
Sur un échiquier n·n, le maximum de tours
indépendantes avec pions est:
Pour les fous ce
serait:
|
|
|
Exemples sur un échiquier 8x8
8 tours et 0 pion / 9 tours et 1 pion / 12 tours et 4 pions Exemples sur un échiquier 9x9
25 tours et 16 pions Bien sûr, il est possible d'en ajouter dans les angles. Développements théoriques dans la
référence du Scientific research |
||
|
Cas des polyominos |
||
|
Un polyomino est
assemblage de carrés élémentaires adjacents. Le défi est
le même: combien de tours indépendantes (ou insaisissables) au maximum ?
Objet de recherches théoriques y compris en trois dimensions (polycubes). Deux
exemples simples en illustration. |
|
|
|
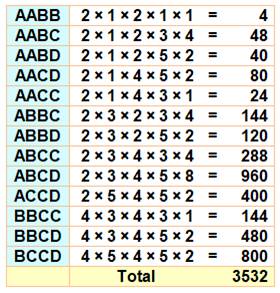
Pour quatre tours Combien de possibilités pour placer les quatre
tours sur ce morceau d'échiquier ? Combien de configurations indépendantes ? Quatre tours sur ce morceau
d'échiquier On compte les possibilités selon la combinaison
des quatre colonnes:
Exemple de calcul pour ABCD: 2 (4 – 1) (6 –
2) (8 – 3) = 2 × 3 × 4 × 5; En plus, il existe 2 colonnes A, B, C et une seule D: soit: 2 × 2 × 2 × 1 = 8. D’où la
ligne complète: 2 × 3 × 4 × 5 × 8 = 960. |
Exemple de quatre tours
indépendantes sur ce sous-ensemble d'échiquier
Avec ce morceau d'échiquier, il
y a
|
||
|
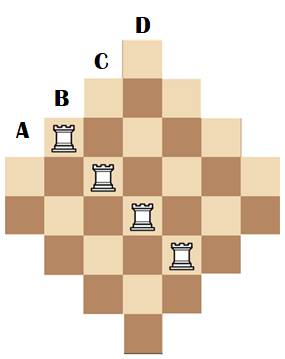
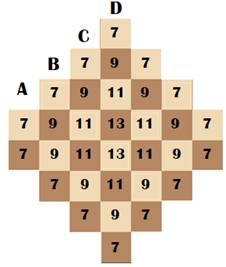
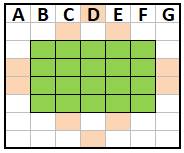
Quatre tours indépendantes Toutes les positions ne sont pas possibles. Sur l'exemple de gauche, la position 1 maitrise
sept cases. La colonne B doit être maitrisée par la position 2, par exemple.
Impossible de maitriser toutes les autres avec les deux tours restantes. Même chose pour 1 et 2 sur les exemples du centre
et de droite.
Finalement, les seules positions possibles sont
celles du rectangle vert. Une tour possible par ligne: soit 4 x 3 x 2 x 1 =
4! = 24 possibilités de tours indépendantes. Avec cinq colonnes pour quatre couvertes par les tours,
il existe plusieurs configurations: BCDE, BCDF, … soit 1 "trou" parmi 5 = 5
possibilités. Total: 5 x 24
= 120 possibilités de tours indépendantes. |
Carte de la puissance de la tour
selon son emplacement
Les seules positions autorisées
|
||
Anglais
|
Problem of the independent rooks (or towers): In how many different ways
can we place 8 identical rooks on a chess board so that no two of them attack
each other? How many possibilities
are there where no tower can beat another tower, i.e no more than one tower
on each row and column? Chessboard recreation: in
how many ways can a given number of rooks be placed on a chessboard so that
no two attack each other? |
Voir
Anglais pour le bac et pour les affaires
![]()
Graphe de déplacements des tours – Théorie *
|
Représentation des mouvements de la tour pour chaque position.
Ce graphe
est hautement symétrique. Il est parfait: chaque
sous-ensemble de cellules de l'échiquier peut être coloré de manière à ce que
deux cases d'une ligne ou d'une colonne n'aient pas la même couleur, et de
sorte que le nombre de couleurs soit égal au nombre maximum de cases du
sous-ensemble dans une seul ligne ou colonne (le numéro de clique d'un sous-graphe
induit). Les graphes
ainsi formés à partir de sous-ensembles de carrés dans un graphe de tours
forment l'un des composants clés d'une décomposition de graphes parfaits
utilisés pour prouver le théorème du graphe parfait fort caractérisant tous
les graphes parfaits. Le nombre
d'indépendances et le nombre de dominations d'un graphe de tours, ou en
d'autres termes le nombre maximum de tours qui peuvent être placées de
manière à ce qu'elles ne s'attaquent pas les unes aux autres ou à ce qu'elles
attaquent toutes les cases restantes de l'échiquier, toutes deux sont égales
à la plus petite des deux dimensions de l'échiquier, et ce sont des graphes
bien couverts, ce qui signifie que placer des tours non attaquantes une à la
fois ne peut jamais rester bloqué tant qu'un ensemble de taille maximale
n'est pas atteint. |
Source:
Rook's graph –
Wikipedia
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
|
Voir |
|
|
|
|
||
|
Cette page |
||