NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/11/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Jeux et problèmes
Débutants Général	ÉCHECS			Glossaire Général
INDEX Jeux Jeux avec lettres et nombres	Introduction & invention	Solutions	Cavalier	Dame / Reine
		Pavage	Tour	Fou
		Sommaire de cette page >>> Balayage de dame/reine >>> Pions non-alignés >>> Problème des huit dames >>> les 12 solutions primaires >>> Les 92 solutions >>> Correspondance avec les solutions Wikipédia >>> Quantité de solutions >>> Anglais >>> Jeu

DAME aux ÉCHECS

Le problème des huit dames ou des huit reines est classique car il se prête bien à une initiation informatique, notamment pour apprendre la notion de récursivité.

Problème formalisé en 1848 par le joueur d'échecs Max Bezzel.

	Dame ou Reine ? C'est DAME !
Mais, le mot reine est souvent utilisé du fait que cette pièce est nommée Queen (Reine) en anglais. Ce n'est qu'à la fin du Moyen Âge que la "reine" devient d'un emploi courant. Avant se trouvait le vizir. Flottement entre les deux pièces jusque vers 1200. La dame est aujourd'hui la pièce la plus puissante de l'échiquier. Elle ne se déplaçait que d'une case, comme le roi. C'est au XV^e siècle que la dame s'est déplacée sur toute l'envergure de l'échiquier.

Historique

Le problème de l'indépendance de la dame sur l'échiquier a été étudié pour la première fois en 1848 par Max Bezzel, puis généralisé aux pièces de l'échiquier.

En 1850, Franz Nauck publie les premières solutions toute en étendant le problème à un échiquier n·n. D'autres contributeurs suivront: Gauss, Gunther (1874), Glaisher (1960).

En 1972, Edsger Dijkstra utilise le problème des reines pour montrer la puissance de la programmation structurée.

Des variantes incluant des pions sont parfois étudiées. Par exemple, Zhao a montrer qu'il est possible de placer plus de n dames sur n échiquier n·n en plaçant des pions bloquants. On en place six sur un échiquier 5x5 en introduisant trois pions (conditions nécessaire et suffisante). Voir cas de la tour

Anglais

The topic of independence on chessboard graphs was first considered in 1848 by chess composer and enthusiast Max Bezzel, when Bezzel considered the queen’s independence problem on the standard board.

Voir Problème de l'indépendance des tours

Voir les références pour les sources de ces informations

Balayage de dame
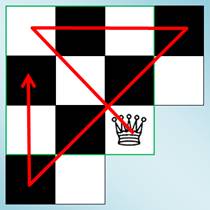
Problème Faire passer la dame sur 3 x 3 cases en seulement 4 mouvements.	Solution Il y a une astuce: utilisation de deux cases supplémentaires sur le damier.

Pions non-alignés

Caractérisation de l'énigme

Pions non-alignés

Grille

Raisonnement

Classique

Primaire

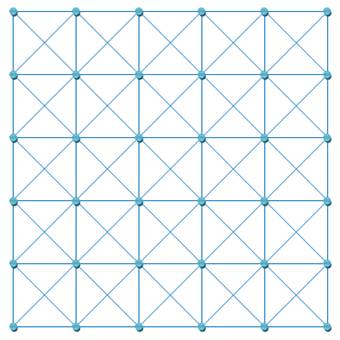
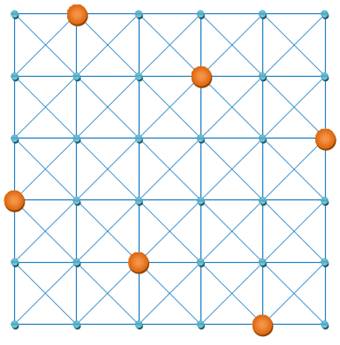
Énigme

Combien de pions au minimum peut-on placer sur les sommets des carrés (points bleus) sans que deux pions soient sur la même ligne ?

Réponse

Maximum six pions.
Un sur chaque ligne et sur chaque colonne avec décalage.

Cette énigme est du même type que celle des huit reines.

Problème des huit dames / reines

Eight queens puzzle

Caractérisation de l'énigme

Problème des huit reines

Grille

Raisonnement

Classique

Primaire

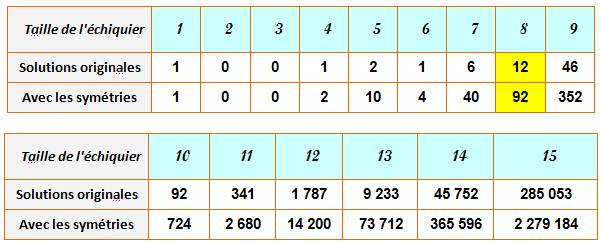
Problème des huit reines

Il est possible de placer huit dames sur un échiquier sans qu'elles ne s'attaquent les unes les autres (on ne tient pas compte de la couleur de la dame).

Autrement dit: placer huit dames sur des lignes, colonnes et diagonales différentes.

Solutions
Il y a 12 manières différentes de résoudre ce problème;
ou 92 avec toutes les symétries.

Les douze solutions primaires

Remarque

Il y a bien une reine par ligne et une reine par colonne. Observation utile pour réaliser un algorithme de résolution. Attention, ce n'est pas vrai pour les pandiagonales (diagonales reconstituées par enroulement).

Les quatre-vingt-douze solutions avec rotations et réflexions

En rouge, les solutions explicitées ci-dessus; En dessous, les solutions déduites par rotations (90°, 180° et 270°). Dans la colonne plus à droite: la solution(Sol) précédente, mais inversés (Los).

Soit, huit solutions pour chaque solution primaire (8 x 12 = 96), en remarquant que les symétries de la solution 1, il faut retirer quatre solutions redondantes (96 – 4 = 92)

Lecture des solutions: Implicitement chaque chiffre est précédé des lettres A, B, C, …dans l'ordre.

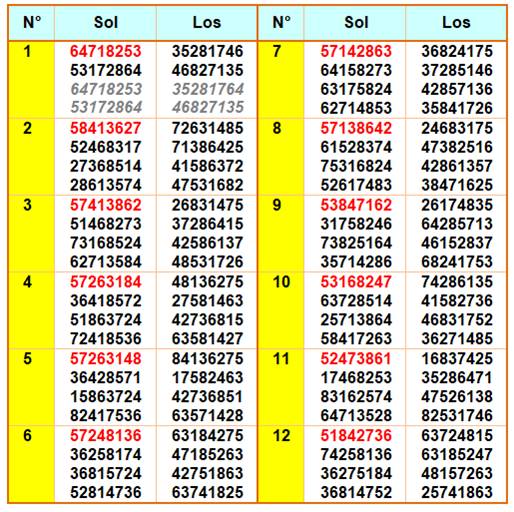
Correspondance avec les solutions présentées sur la page Wikipédia

QUANTITÉ DE SOLUTIONS selon la taille de l'échiquier

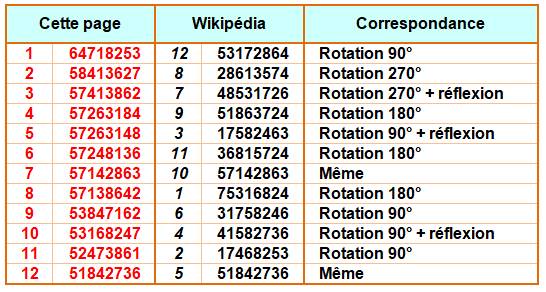
Voir Nombre 92

Jeux en ligne

Vous pouvez jouez au problème des huit dames sur Internet:

8 Queens - Brain metrix – Train the Brain: jeu en ligne qui a l'avantage de montrer les positions tenues par toute nouvelle reine introduite sur l'échiquier.

Exemple de résolution

Eight queens problem – H.B. Meyer – La position tenue par chaque reine est aussi visualisée. Un mode permet de finir la solution automatiquement.

Existe aussi sous le nom FRUSTR8TOR (the Amazing Braingame). Invention d'Albert Eckhardt.

Vous pouvez aussi vous essayer à la programmation de ce jeu. Un million de dollars est offert par le Clay Mathematics Institure à celui qui trouvera un algorithme capable de résoudre le cas 1000x1000 réalisable en un temps raisonnable sur ordinateur.

English corner
The eight queens puzzle is the problem of putting eight chess queens on an 8 8 chessboard such that none of them is able to capture any other using the standard chess queen's moves.

Merci à Jos Heynderickx pour tous les compléments apportés à cette page

Suite	Fou Voir haut de page
Voir	Carrés magiques Champions et machines Échiquier et lettres Graphes Intelligence artificielle Jeux et énigmes – Index Morpions Œil et cerveau Pentominos Roméo et Juliette Solitaire
Sites	Problème des huit dames - Wikipédia Eight queens puzzle – Wikipedia The 8 Queen problem – Numberphile (vidéo) Squeens.txt – Liste de toutes les solutions A generating function with maximum combination of rook and bishop movement on a two-dimensional chess board is also a maximum queen movement – M. Laisin & Okaa-Onwuogu
Algorithme et programmation	Algorithme III – le problème des huit reines Queens problem and its visualization with Maple Eight Queens Puzzle Solution Using MATLAB Eight Queens – DataGenetics – Jeux / Toutes les solutions / Algorithme / Quantité de solutions selon taille de la grille
Cette page	http://villemin.gerard.free.fr/Puzzle/EchecDam.htm