NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/02/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Jeux et problèmes
Débutants Général	ÉCHECS			Glossaire Général
INDEX Jeux Jeux avec lettres et nombres	Introduction & invention	Solutions	Cavalier	Dame / Reine
		Pavage	Tour	Fou
		Sommaire de cette page >>> Puissance du fou >>> Attaque des fous >>> Généralisation

Parcours le long pour un fou

29 cases au maximum

Puissance du FOU
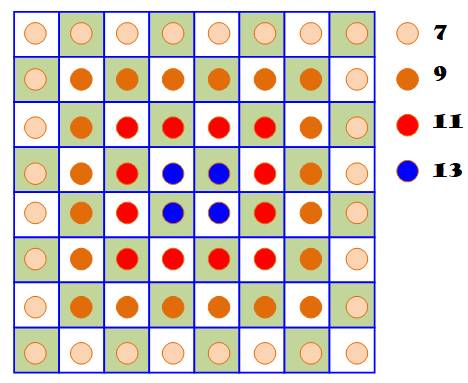
Pour chaque case, on compte la quantité de cases maitrisées par le fou. On compte, la quantité de cases situées sur les deux diagonales passant par la case concernée. Ainsi, la case située dans chaque coin maitrise sept cases. La case suivante en bordure en maitrise 6 + 1 = 7.

Anglais: bishop power

ATTAQUE DES FOUS

Nombre de manière d'arranger des fous sur un échiquier sans prise l'un part un autre

On peut mettre 14 fous sur l'échiquier de 8 x 8.

Il y a, en fait, 256 possibilités sans éliminer les symétries et rotations.

Exemples

F
F	F
F	F
F	F
F	F
F	F
F	F
F

		F
F			F
F			F
F
			F
F			F
F			F
F	F		F

GÉNÉRALISATION

Sur un échiquier de n x n, on peut mettre 2n - 2 fous de 2ⁿ manières.

En fait, de d manières distinctes, avec: 

si n est pair:	d = 2^n-4 / 2	x (2^(n-2)/2 + 1)
si n est impair:	d = 2^n-3 / 2	x (2^(n-3)/2 + 1)

Calcul

n	nombre de Fous	Nombre de solutions	d = nombre de solutions distinctes	Ratio
2	2	4	1	400
3	4	8	2	400
4	6	16	3	533
5	8	32	6	533
6	10	64	10	640
7	12	128	20	640
8	14	256	36	711
9	16	512	72	711
10	18	1 024	136	752
11	20	2 048	272	752
12	22	4 096	528	775

Suite	Introduction & invention Voir haut de page
Voir	Carrés magiques Échiquier et lettres Graphes Intelligence artificielle Jeux et énigmes – Index Morpions Œil et cerveau Pentominos Roméo et Juliette Solitaire
Cette page	http://villemin.gerard.free.fr/Puzzle/EchecFou.htm