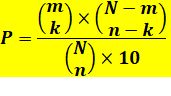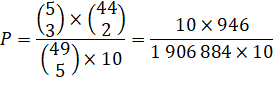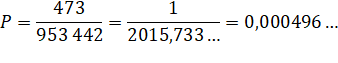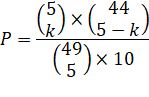|
||||||||||||||||||||||||||||||||
![]()
|
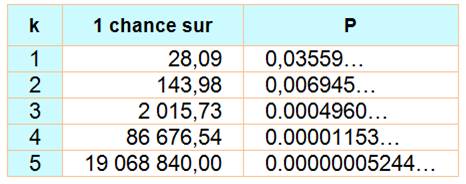
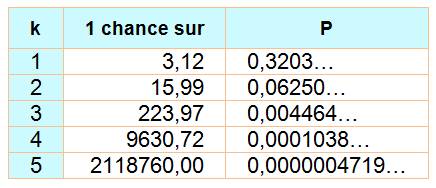
LOTO Français Deuxième rang et suivants La probabilité de gagner le jackpot
(premier rang) est un simple calcul de combinaisons.
La probabilité de gagner aux rangs suivants fait appel à la loi hypergéométrique. Il faut non seulement
compter sur les n numéros gagnants, mais
aussi sur les 5 – n numéros non-gagnants. On donne d'abord les valeurs pour le loto français et le Lotto belge
>>> Puis les explications pour appliquer la formule de calcul >>> |
Comparaison
Loto français et Lotto belge
Comparaison:
valeurs données sur les sites Internet et valeurs calculées avec la formule
ci-dessous
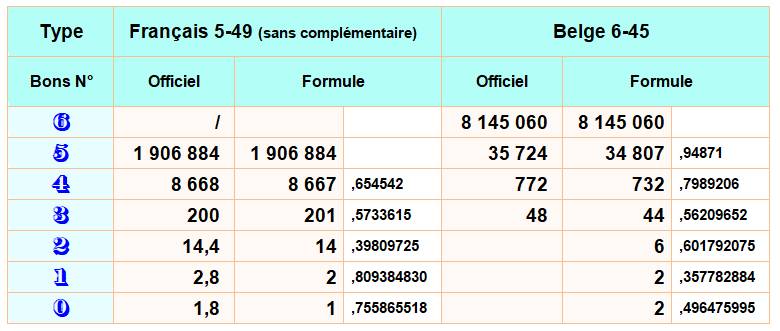
Loto français: aucune différence;
Lotto belge quelques divergentes (explications?)
|
|
||
|
Programme
|
Commentaires Exemple avec le Lotto belge (6 boules et 45 numéros) et, ici, calcul
de la probabilité pour 5 boules gagnantes. On utilise le groupe-logiciel "combinat" qui donne la
quantité de combinaison avec l'instruction numbcomb. Résultats - la fraction donnant la probabilité - sa valeur numérique son inverse qui donne la quantité de chance: ici, une chance sur 34
808. |
|
Voir Programmation
![]()
|
3 bons numéros + n° chance
(loto) |
|
||||
|
Exemple: trois bons
numéros dans un tirage de cinq parmi les 49 boules plus le bon numéro chance
(1 parmi 10). |
|||||
|
|
N
= 49 m
= 5 m'
= N – m = 44 |
||||
|
|
n
= 5 |
||||
|
|
k
= 3 |
||||
|
|
|
Tirées |
Laissées |
Total |
|
|
Voulues |
k
= 3 |
m
– k = 2 |
m
= 5 |
||
|
Non
voulues |
n
– k = 2 |
m'
– (n–k) = 40 |
m'
= 44 |
||
|
Total |
n
= 5 |
N
– n = 43 |
N
= 49 |
||
|
|
Soit
1 chance sur 2016 (arrondi). |
||||
|
|
||
|
Pour
k bons numéros avec n°chance: formule et
tableau |
|
|
|
Pour
k bons numéros sans le numéro chance. C'est 9 fois moins que le gain avec le
numéro chance. |
Si
le numéro chance était gagnant à chaque fois, la probabilité de gain serait
10 fois P. La
probabilité de gagner avec le numéro
chance étant P, la probabilité de ne pas gagner
avec ce numéro est 10P – P = 9 P
|
|
|
Comme
le montre le tableau en tête, la formule s'applique
dans tous les cas. De 5 à 0 numéros trouvés dans le cas du loto français. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()