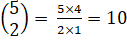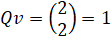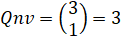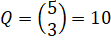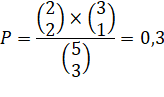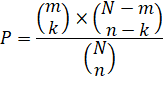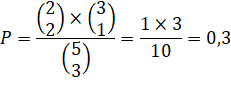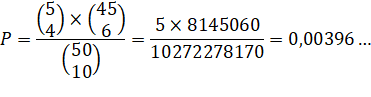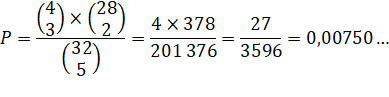NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/07/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER
Débutants Dénombrer	COMBINAISONS			Glossaire Combinatoire
INDEX Combinatoire		Général	Hypergéométrique
		Sommaire de cette page >>> Approche >>> Principe du calcul >>> Tirage 2 sur 3 dans 5 >>> Illustration >>> Tirage 4 sur 10 dans 50 >>> Tirage 3 sur 5 dans 32 (cartes) >>> Bilan

LOI HYPERGÉOMÉTRIQUE

Formule permettant de calculer la probabilité d'un tirage dans un tirage. Par exemple avoir trois bons numéros dans un tirage de 6 parmi 49 (loto). Ou encore, avoir trois rois dans une donne de six cartes d'un jeu de 32 cartes. Etc.

Où il est question de compter la chance, sans oublier: la malchance …

Veuillez ne pas vous attacher au nom barbare de cette formule …

Approche

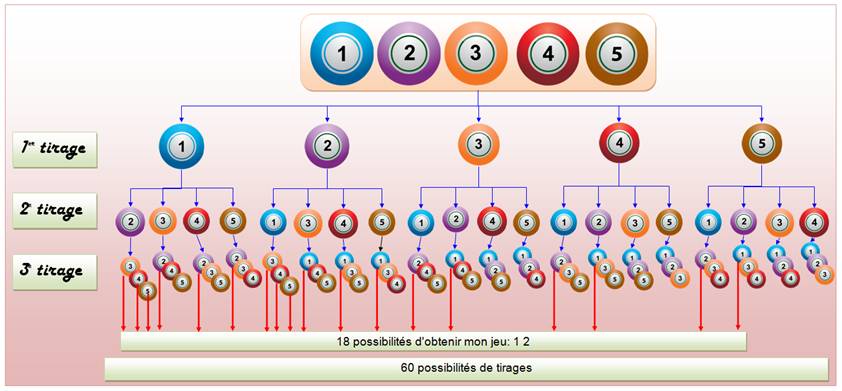
Nous disposons de 5 boules et en tirons 3. Quelle est la probabilité que nous nous retrouvions avec les boules 1 et 2? Illustration Calcul La probabilité est de 18 cas favorables sur 60 cas possibles. Soit: P = 18/60 = 3/10 = 0,3 = 30% Remarque très importante Ici, nous tirons trois boules et nous regardons, parmi les trois boules, si je dispose de celles que j'ai choisies (18 cas sur 60). Ce n'est pas du tout la même chose que si nous tirions deux boules et regardions si nous disposons de notre configuration. En s'arrêtant au deuxième tirage, l'illustration montre qu'il y a seulement 2 cas avec 12 et 21 sur les 20 tirages possibles. Probabilité: 2/20 = 1/10 = 0, 1 = 10% Le calcul des combinaisons corrobore cette valeur: . Soit une chance sur 10.

Principe du calcul
Nous cherchons notre configuration (ici 1 2 ou 2 1), à l'exception de tous les autres. Ce qui fait une combinaison.	Cas où l'on a 1 2 ou 2 1 Cas où il n'y a pas 1 2 ou 2 1
Les deux boules que nous cherchons nous les voulons toutes les deux. Il y a seule combinaison
La troisième boule ne doit pas être celle que nous cherchons
La quantité totale de combinaisons
Probabilité
Généralisation avec N la quantité totale de boules (N = 5) n la quantité de boules tirées (n = 3) m la quantité de boules ayant le critère voulu (m = 2) m' = N – m la quantité de boules n'ayant pas le critère voulu (m'= 3) k la quantité de boules voulues (k = 2) k' = n – k la quantité de boules non voulues (k' = 1)

Tirage 2 sur 3 dans 5 (formalisation du cas précédent)
Dans l'urne, il y a N boules dont m ayant le critère voulu (ici, deux boules, la 1 et la 2), et m' = N – m de critère non voulu.			N = 5 m = 2 m' = N – m = 3
Nous tirons n boules successivement sans les remettre dans l'urne.			n = 3
Notre désir est de savoir dans combien de cas, j'en tirerai 2 voulues.			k = 2 k' = 1
Tableau de la situation.		Tirées	Laissées	Total
	Voulues	k = 2	m – k = 0	m = 2
	Non voulues	n – k = 1	m' – (n–k) = 2	m' = 3
	Total	n = 3	N – n = 2	N = 5
Calcul de probabilité: formule générale et application numérique.

Illustration

Tirage 4 sur 10 dans 50
Dans l'urne, il y a N boules dont m blanches, et N – m noires.			N = 50 m = 5 m' = N – m = 45
Nous tirons n boules successivement sans les remettre dans l'urne.			n = 10
Notre désir est de savoir dans combien de cas, j'en tirerai k blanches.			k = 4
Tableau de la situation.		Tirées	Laissées	Total
	Blanches	k = 4	m – k = 1	m = 5
	Noires	n – k = 6	m' – (n–k) = 39	m' = 45
	Total	n = 10	N – n = 40	N = 50
Calcul de probabilité: formule générale et application numérique.

Tirage 3 sur 5 dans 32
Dans le jeu il y a N cartes dont m = 4 rois et N – m non voulues.			N = 32 m = 4 m' = N – m = 28
Nous tirons n cartes.			n = 5
Notre désir est de savoir dans combien de cas il y aura un brelan de rois (3 rois précisément)			k = 3
Tableau de la situation.		Tirées	Laissées	Total
	Voulues	k = 3	m – k = 1	m = 4
	Non voulues	n – k = 2	m' – (n–k) = 26	m' = 28
	Total	n = 5	N – n = 27	N = 32
Calcul de probabilité: formule générale et application numérique.

Bilan

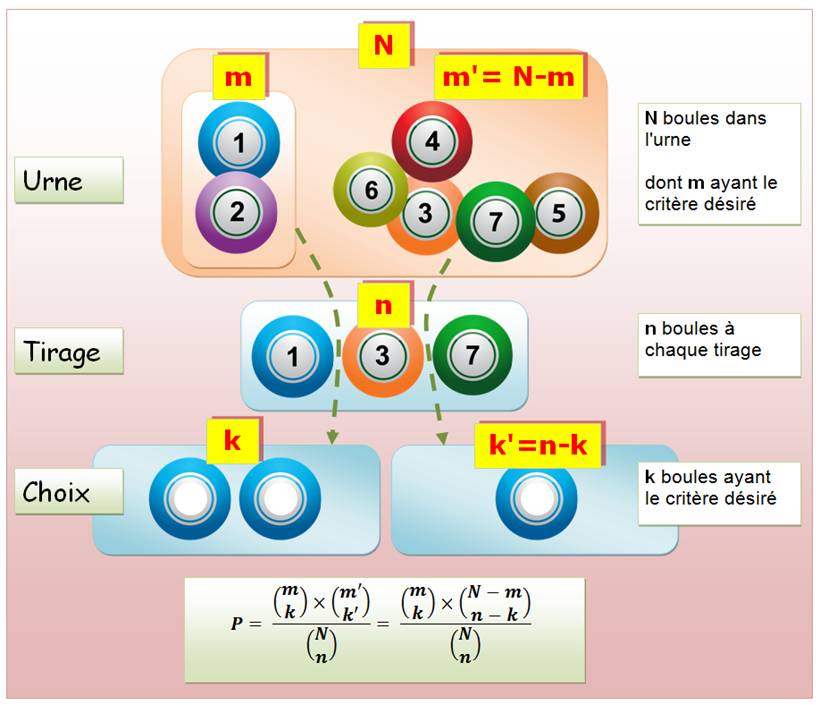
Si l'on veut faire un choix dans un tirage, le calcul exige de compter les cas où le choix est réussi et les cas où le choix n'est pas réussi.

Attention, le fait que le choix s'effectue à l'intérieur d'un tirage, exige un peu d'attention. Le résultat n'est pas direct. C'est la formule de la loi hypergéométrique qui s'applique.

Suite	Combinaisons Loto
Retour	Combinatoire – Rubriques D'un coup d'œil
Voir	Cartes Compter les nombres Dés Dominos Échecs Factorielle et ses cousines Grenouilles Jeux Probabilités Triangle de Pascal
Cette page	http://villemin.gerard.free.fr/Denombre/Hypergeo.htm