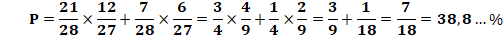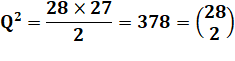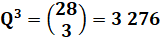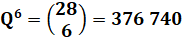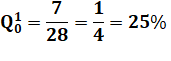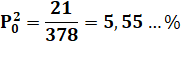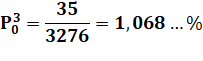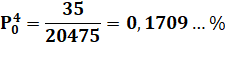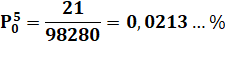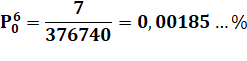|
Édition du: 02/03/2023 |
|
INDEX |
JEUX – DOMINOS |
||
|
Dominos (le jeu) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
DOMINOS & Probabilités Dénombrement
avec des dominos, comme par exemple: combien de possibilités de tirer trois
dominos, chacun comportant un "0" ? Exemple: probabilité
de tirer les sept dominos comportant chacun un zéro (ou un autre nombre): moins
de une chance sur un million >>>
|
||
|
|
Sommaire de cette page >>> Dénombrement des dominos >>> Deux dominos qui se suivent
>>> Résumé >>> Probabilité de 1 fois le "0" >>> Probabilité de 7 fois le "0" >>> Probabilité de 2 fois le "0" >>> Probabilité de 3 fois le "0" >>> Probabilité de 4 fois le "0" >>> Probabilité de 5 fois le "0" >>> Probabilité de 6 fois le "0" >>> Programmation Maple |
Débutants Glossaire |
Astuce: doubler les dominos pour former un rectangle
de 7 ×
8
Quantité de dominos: (7 ×
8) /2 = 28

Deux dominos qui se
suivent. Un petit exercice de probabilité
|
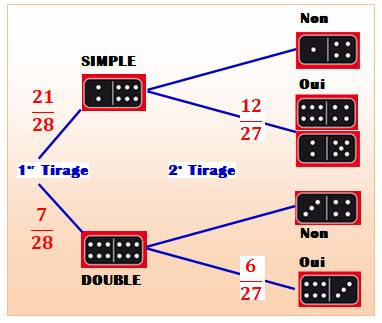
Quelle
est la probabilité que, ayant tiré domino, le second puisse convenir selon la
règle Au
premier tirage, la probabilité de tirer un domino simple est 21/28 et celle
d'un double est 7/28. Dans
le premier cas, la probabilité de tirer un domino qui peut prendre la suite doit
contenir le 6 ou le 2, et il en reste 6 de l'un et 6 de l'autre sur 27
dominos encore sur le tapis. Probabilité: 12/27. Dans
le second cas, seul le 6 convient. Il en reste 6 sur 27 dominos. Probabilité:
6/27. Les deux
cas sont indépendants et, c'est soit l'un soit l'autre, alors les probabilités
s'ajoutent.
En gros: une chance sur trois que les deux dominos se
suivent. |
|
Combinaisons avec les dominos Exemple de
tirages de deux dominos 0-0 & 0-1 0-0 & 0-2 0-0 & 0-3 0-0 & 6-5 0-0 & 6-6 … 0-1 & 0-2 0-1 & 0-3 … 0-4 & 6-5 0-5 & 6-6 |
En choisissant UN
domino parmi vingt-huit, il y a évidemment 28 possibilités.
En choisissant DEUX
dominos parmi vingt-huit, il y a 28 possibilités pour le premier et il en
reste 27 pour le second. Mais attention à ne compter 0-1 et 1-0 qu'une
seule fois. D'où la division par 2. C'est, bien sûr, la quantité de combinaisons
de 2 parmi 28.
Autre façon de compter: avec le 0-0 sont associés
27 dominos; avec le 0-1, il en reste 26; avec le 0-2, c'est 25; etc. Soit la somme des entiers:
En choisissant TROIS
dominos parmi vingt-huit, on a:
Etc. La quantité de possibilités lors d'un tirage de k
dominos parmi vingt-huit est donc le kième coefficient sur la ligne 28 du triangle de
Pascal. |
||
|
Ligne 28 du triangle de Pascal L'indice
donne la valeur de k |
00, 281, 3782, 32763,
204754, 982805, 3767406, 11840407,
3108105, 6906900, 13123110, 21474180, 30421755, 37442160, 40116600,
37442160, 30421755, 21474180, 13123110, 6906900, 3108105, 1184040, 376740,
98280, 20475, 3276, 378, 28, 1 |
||
|
Exemple avec six dominos Exemple de l'un des tirages
|
Il y a 376 740 façons de tirer six dominos dans
un jeu de vingt-huit. |
||
Résumé
des calculs détaillés ci-dessous
|
On dénombre les cas où k dominos comportent tous le nombre
"0". Évidemment, les résultats sont identiques pour chacun des autres
nombres.
Ainsi, par exemple, il existe sept tirages de un domino pour lesquels
ce domino comporte un "0". Autre exemple: il y a vingt-et-un tirages de deux dominos chacun avec
un "0". |
|
Un seul domino "0" Le jeu de dominos est retourné. On tire un domino. Quelle est la
probabilité d'obtenir le domino portant un "0" ? |
Le jeu de dominos comporte vingt-huit pièces dont
sept avec le numéro "0": 0-0, 0-1,
0-2, 0-3, 0-4, 0-5, 0-6. On a donc sept chances sur vingt-huit de tirer un
domino avec un "0".
|
|
|
|
||
|
Un sept dominos "0" Le jeu de dominos est retourné. On tire sept dominos. Quelle est la
probabilité d'obtenir les sept dominos portant un "0" ? Ce sera aussi la probabilité appliquée à n'importe quel autre chiffre que
"0", et même à l'obtention des sept dominos doubles. Rappel du
calcul des tirages possibles: (27×26×25×24×23×22) / 7! = 1 184
040 Voir la note ci-contre |
Le jeu ne comportant que sept dominos avec un
"0", le seul cas favorable est celui où on a la chance de retourner
tous ces sept dominos. Donc une seule chance. Sur combien ? Toutes les
combinaisons de choix de sept dominos parmi vingt-huit sont à considérer. La probabilité cherchée est donc une chance sur 1
184 040. En gros: moins d'une chance sur un million. Dit autrement: si on disposait toutes les 1 184 040
façons de regrouper sept dominos parmi les vingt-huit sur une (grande) table,
une seule configuration présenterait les sept dominos avec "0". Note:
pourquoi 7! En faisant le produit 27×26×…×22, on
compte toutes les combinaisons à sept dominos, y compris celles qui sont le
mélange les unes des autres. Or, la quantité de ces combinaisons identiques à
l'ordre près est: 7×6×5×4×3×2×1 = 7! = 5
040. |
|
|
Un des sept dominos "0"
ou "1" ou "2" ou … Et la probabilité d'un tirage du même numéro pour les sept dominos ? |
Imaginons sept joueurs et sept jeux de dominos.
Chacun tire les dominos et cherche à faire le numéro de son rang, de 0 à 6. Le premier à une chance sur 1 184 040 de tirer le
"0". Le deuxième à une chance sur 1 184 040 de tirer
le "1". Pour les sept joueurs, la probabilité de trouver
un jeu complet d'un numéro donné sera: 7 chances sur 1 184 040, soit 0,000591… %. (une chance sur 170 000, environ). Dit autrement: si on disposait toutes les 1 184 040
façons de regrouper sept dominos parmi les vingt-huit, on y trouverait
chacune des configurations avec le même numéro pour les sept, mais chacune
des configurations une fois seulement.
|
|
|
|
||
|
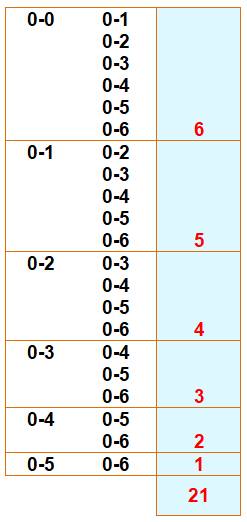
Un seul numéro avec deux dominos Le jeu de dominos est retourné. On tire deux dominos. Quelle est la
probabilité d'obtenir les deux dominos portant un "0" ? Dénombrement Le tableau montre toutes les possibilités. Pour un total de 21 cas favorables. Sur 378 tirages Probabilité:
Soit, une chance sur 18. Commentaires Avec le domino 0-0, il y a 6 possibilités de tirer un autre domino
portant le numéro "0". Avec le 0-1, il ne reste que 5 possibilités. Etc. La somme des entiers de 1 à 6 vaut: 6 x 7 / 2 = 21. |
|
|
|
|
||
|
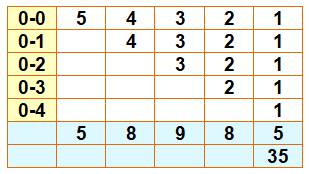
Un seul numéro avec trois dominos Le jeu de dominos est retourné. On tire trois dominos. Quelle est la
probabilité d'obtenir les trois dominos portant un "0" ? Dénombrement Le tableau montre toutes les possibilités. Avec le 0-0 et
Avec le 0-1 et
Jusqu'au 0-4 pour lequel les seuls qui restent sont le 0-5 et le 0-6. |
Soit une chance sur 93. |
|
|
|
||
|
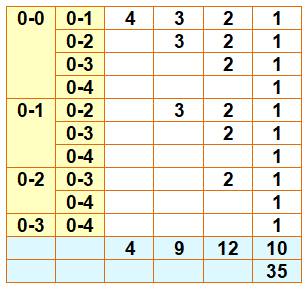
Un seul numéro avec quatre dominos Quelle est la probabilité d'obtenir les quatre dominos portant un
"0" ? Dénombrement Le tableau montre toutes les possibilités. Avec les 0-0 et 0-1, il y a:
Avec les 0-0 et 0-2, il y a:
Etc. |
Soit une chance sur 585. |
|
|
|
||
|
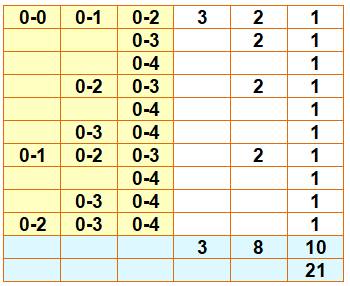
Un seul numéro avec cinq dominos Quelle est la probabilité d'obtenir les quatre dominos portant un
"0" ? Dénombrement Le tableau montre toutes les possibilités. Cette fois on dresse trois colonnes pour représenter la configuration
des trois premiers dominos et les colonnes de droite montrent les possibilité
pour les deux dominos suivants. |
Soit une chance sur 4680. |
|
|
|
||
|
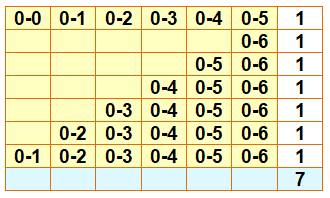
Un seul numéro avec six dominos Quelle est la probabilité d'obtenir les quatre dominos portant un
"0" ? Dénombrement Le tableau montre toutes les possibilités. Elles sont peu nombreuses et toutes les configurations sont listées. |
Soit une chance sur 52534. |
|
|
|
But Lister et compter toutes les configurations de
trois dominos, chacun comportant un "0". Un petit exercice de programmation qui permet de
vérifier la justesse du dénombrement. Commentaires Initialisation avec restart. Liste des 28 dominos dans la liste R. Trois boucles pour balayer tous les dominos. De 1
à 28, puis de a+1 à 28 et de b+1 à 28 pour le troisième. Détection de la présence (member) d'un zéro dans chacun des dominos qui sont en cour
d'analyse. Si c'est le cas impression et incrémentation du
compteur kt. Fin des trois boucles en écrivant do à l'envers. Impression de la valeur de kt du fait de la
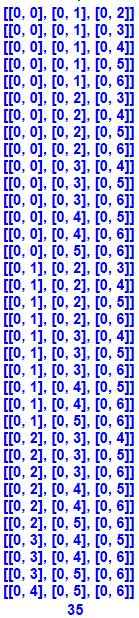
présence d'un ";". Résultats Liste des 35 configurations à trois
"0". Autre cas Pour plus de dominos avec "0", ajouter
des boucles de balayages et aménager le programme en conséquence. |
|
Voir Programmation – Index
Haut de page (ou
double-clic)
![]()
|
Retour |
||
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
||