|
|||||||||||||||||||||||||||||
![]()
|
Pavage MINIMAL du RECTANGLE avec des DOMINOS Un jeu amusant au début, un
problème sérieux de mathématique dans la rubrique des pavages (tilings). Il s'agit de paver un rectangle
avec des dominos, sans faire apparaître de lignes droites horizontales ou
verticales coupant le rectangle en deux. C'est un pavage
sans défaut ou sans faute. Un peu à la manière de la construction d'un
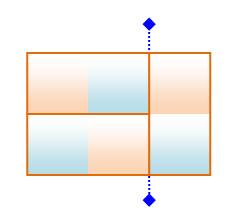
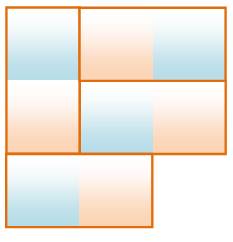
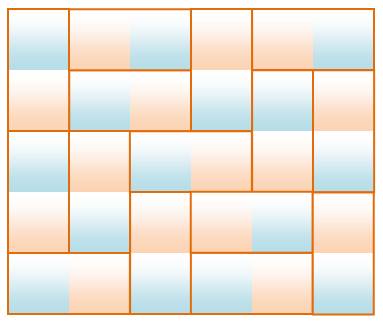
mur sans coupure verticale qui compromettrait la solidité de ce mur. La solution minimale: rectangle 5 x 6 >>> |
Anglais: Fault-free tilings of rectangle
|
|
||
|
Rectangle 2 x 3
Rectangle 2 x 4
Rectangle 2 x 5 Impossible. Toujours quatre dominos couchés et un
debout. |
Aucun de ces pavages ne répond à notre critère. |
|
|
|
||
|
Rectangle 3 x 3
Rectangles impair-impair
impossibles à paver sans défaut avec des dominos. |
|
|
|
|
||
|
Rectangle 3 x 4
Rectangle 3 x 5
Rectangle 3 x 6
|
Ne répondent toujours pas à notre critère de ligne sécante
non-autorisée |
|
|
|
||
|
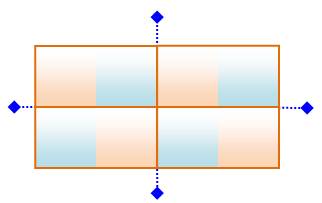
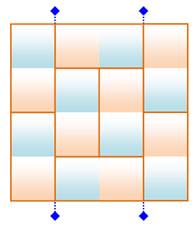
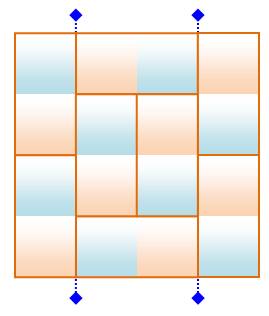
Rectangle pair-pair (ici: 4
x 4)
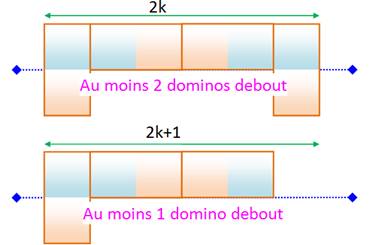
Deux théorèmes Sur une dimension paire,
nous trouverons 2k dominos debout Sur une dimension impaire,
nous trouverons au moins 1 domino debout. |
|
|
|
|
||
|
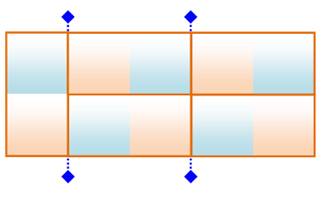
Rectangle 4 x 4
Notez pour la suite
que le nombre de lignes est égal à 4 – 1; un de moins que la dimension. Rectangle 4 x 5
Rectangle 4 x 7
|
Toujours impossible!
|
|
|
|
||
|
|
Faisabilité d'un rectangle
pair-pair
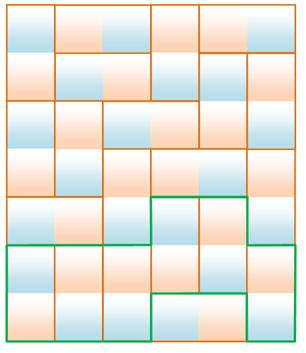
Rectangle 6 x 8 sans faute
|
|
|
|
||
|
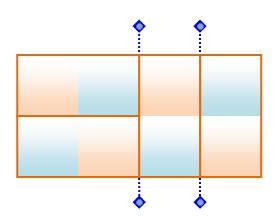
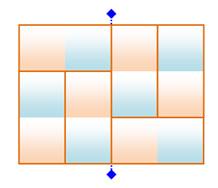
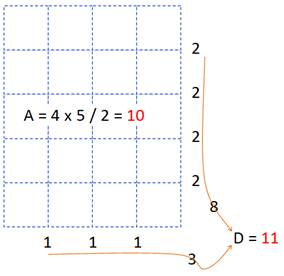
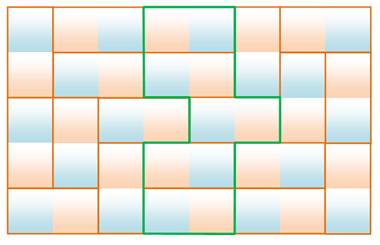
Rectangle 5 x 6
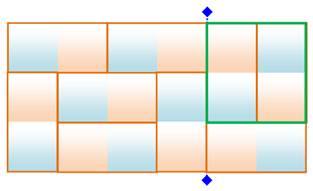
Si le rectangle m x n est une solution, tout
rectangle m x (n + 2k) est aussi une solution. Extension du 5 x 6 en 7 x 6
Si le rectangle m x n est une solution, tout
rectangle (m + 2k') x n est aussi une
solution. |
Solution minimale: 5 x 6
|
|
|
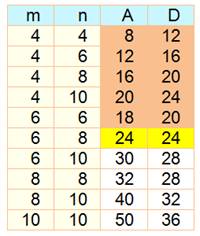
En
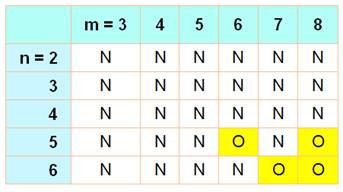
reprenant tous les cas exposés, nous pouvons dresser le tableau suivant:
Théorème de Ron Graham Un rectangle m x n dont l'aire > 2 est une solution du pavage par dominos sans
faute si et seulement si: m m et n non simultanément égaux à 6, et le produit m x n est pair. La démonstration repose sur le
procédé d'extension vu ci-dessus. Généralisation Un rectangle p x q,
pavé par un domino a x b, est une solution du pavage sans faute si et
seulement si:
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()