abécédaire – Fermat -Wiles …

X	Inconnue & Équations	La lettre x est utilisée pour désigner - une inconnue, - une valeur à trouver, dans les équations Elle est le symbole du passage - de l'arithmétique à l'algèbre - du calcul sur les nombres au calcul avec des lettres (calcul symbolique) Les égalités faisant intervenir une ou plusieurs inconnues sont appelées des équations - Une grande part de l'algèbre s'intéresse aux méthodes permettant de trouver les valeurs des inconnues, dites racines de l'équation	Problème de lapins et de canards La fermière compte ses lapins et canards: il y a 7 bêtes pour 24 pattes. Combien de chaque?
			Solution avec l'algèbre - Soit x lapins et y canards - Comptons les animaux x + y = 7 - Comptons les pattes 4x + 2y = 24 - Rapprochons ces deux équations en multipliant la première par 2 4x + 2y = 24 2x + 2y = 14 - Soustraction 2x + 0 = 10 x = 5 - En remplaçant x par sa valeur x + y = 7 5 + y = 7 y = 7- 5 = 2 - Il y a 5 lapins et 2 canards	Solution avec l'arithmétique - S'il n'avait que des lapins, la quantité de pattes serait 7 x 4 = 28 - Il y aurait 28 – 24 = 4 pattes de trop - Cet écart est dû à l'écart de pattes entre les lapins et les canards, soit 2 pattes d'écart par bête - D'où la quantité de canards: 4 / 2 = 2 canards - Et, sachant qu'il y a 7 bêtes 7 – 2 = 5 lapins
		Certains problèmes - Sont traités avec élégance en utilisant un raisonnement purement inductif (calcul arithmétique de tête) - La méthode algébrique est plus systématique, et elle permet de résoudre les cas les plus complexes C'est un outil qui décuple la capacité humaine
	Suite >>>

Secret de deux: secret de Dieu ; Secret de trois: secret de tous

Coordonnées

Système d'axes

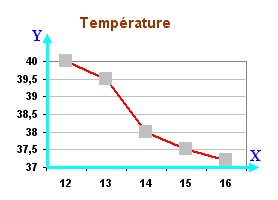
Pour noter la température du malade chaque jour

- Il est classique de reporter ces valeurs sur un graphique

- En horizontal, on indique les jours

C'est l'axe des x ou abscisses

- En vertical, les températures relevées

C'est l'axe des y ou ordonnées

Caractéristiques

- Les deux axes se rencontrent au point origine

- En général, les deux axes sont perpendiculaires

- L'ensemble forme un système d'axes orthonormés

Ce système permet de réaliser une cartographie

- Une visualisation géométrique des expressions algébriques

- Et de résoudre des problèmes autrement très difficiles

La méthode consiste à

calculer la valeur de y pour toutes les valeurs successives de x

reporter ces valeurs sur le système d'axes

une courbe se dessine

elle coupe l'axe des x; notons les valeurs de x

éventuellement, recalculer plus finement jusqu'à obtenir la précision désirée

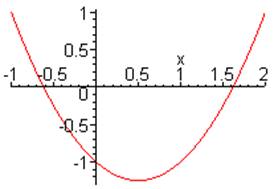
Y = X² - X – 1

Lecture des 2 racines: - 0,62 et 1,62

Valeurs exactes (calculées)

(1 - 5) / 2 = - 0,618 …

(1 + 5) / 2 = 1,618 …

C'est le nombre d'or

L'eau conduit l'électricité, mais si tu mets du vin dedans,

elle n'a plus le droit de conduire

Zéro

Le zéro a deux rôles distincts

- Il occupe les places vides dans les nombres

Dans notre système de numération, le zéro marque l'absence de chiffre significatif

- Il est utilisé dans les opérations

Il fait stagner l'addition et la soustraction

Il remet à zéro toute multiplication

Il joue les trouble-fêtes dans les divisions

Zéro pour les places vides

Mille => 1 000

Mille dix => 1 010

Zéro dans les opérations

1234 + 0 = 1234

1234 – 0 = 1234

1234 x 0 = 0

1234 / 0 = ?? interdit

Suite >>>

Infini

Zéro c'est rien et l'inverse de rien: est-ce l'infini ?

En quelque sorte

Mais on préfère dire que l'inverse de presque rien tend vers l'infini, lorsque ce presque rien est aussi petit que l'on veut

Extraordinaire! Il existe plusieurs sortes d'infinis

- Les nombres entiers sont une infinité

On dit que c'est l'infini dénombrable, car on peut commencer à les compter sans bien sûr pouvoir atteindre l'infini

- Les points d'une droite sont une infinité

On dit que c'est l'infini du continu, comme le tracé de la droite

À chaque point, on peut associer un nombre réel

En première approche disons que les nombres réels sont plus nombreux que les entiers

L'infini du continu et plus grand que l'infini du dénombrable

La puissance du continu est plus grande que celle du dénombrable

L'infini fourmille de paradoxes

- Il y aune infinité (du même type: dénombrable)

de nombres entiers

de nombres impairs

de nombres pairs

de nombres divisibles par 100

de nombres premiers

de nombres fractionnaires (rationnels)

etc.

Approche de l'infini

1 / 0,001 = 1000

1 / 0,000 001 = 1 000 000

1 / 0,000 000 …001 = infini

On note:

lim 1 / = pour 0

Limite de 1 sur epsilon égale l'infini pour epsilon tendant vers zéro

Paradoxe de l'hôtel infini de Hilbert

- L'hôtel infini comporte une infinité de chambres

- Ce soir là, c'est fête et il est plein

- Survient un hôte de marque à qui l'hôtel n'a jamais rien refusé

- Comment le loger?

- Le patron demande au client de la chambre 1 de passer à la chambre 2; le 2 au 3 et ainsi de suite

- La chambre 1 est désormais libre et peut accueillir le VIP

- Vers minuit, surviennent une infinité de clients

- Le patron se débrouille et arrive à les loger. Comment?

- Il place le client de la chambre 1 en 2, celui de 2 en 4, celui de 3 en 6

- Les chambres impaires sont alors libres et peuvent accueillir tous les nouveaux clients

Suite >>>

C'est au moment de payer ses impôts qu'on s'aperçoit qu'on n'a pas les moyens de s'offrir l'argent que l'on gagne - Frédéric Dard

Retour Abécédaire du débutant

Pour poursuivre

Un grand nombre de pages spécialement conçues comme introduction - débutants vous permettront de compléter vos connaissances

Le glossaire et index vous donnera la possibilité de vous envoler vers des notions plus détaillées

Le dictionnaire des nombres vous donnera l'occasion de faire des découvertes en vous amusant

Un cours d'introduction à la théorie des nombres vous donnera la joie d'aborder simplement cette discipline réputée très ardue

et le dictionnaire de base des maths: DicoMot

Voir

Jargon mathématique démystifié

Brèves de Maths

Cette page

http://villemin.gerard.free.fr/Referenc/Debutant/Dico/AlphabeW.htm