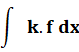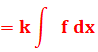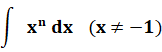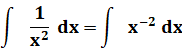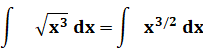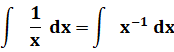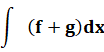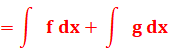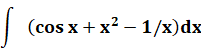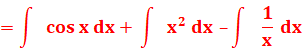|
![]()
|
Image |
Dans un sens L'accélération est la dérivée de la vitesse. La vitesse est la dérivée de la distance
parcourue. Dans l'autre La vitesse est la primitive de l'accélération. La distance parcourue est la primitive de la
vitesse. |
|
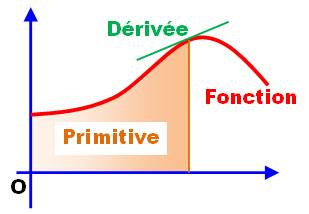
Approche |
Calcul différentiel Il consiste à calculer le taux de variation d'une
grandeur: le taux de variation de la valeur d'une fonction; c'est la dérivée
de la fonction.
Calcul intégral Il consiste à calculer la valeur d'une grandeur
en connaissant son taux de variation: à calculer une fonction en connaissant
sa dérivée; c'est la primitive. De manière
intuitive la dérivée cherche une enveloppe;
alors que la primitive recherche une surface
(calcul d'aire). |
|
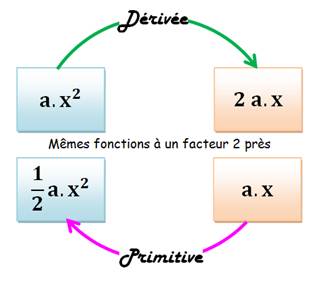
Exemple |
Nous savons
que la dérivée de y = a.x² est y' = 2a.x.
Maintenant, connaissant une fonction dérivée (y'
= a.x), retrouver la fonction (y = 1/2 a.x²). |
|
Formel Relation entre dérivée, fonction et primitive |
|
![]()
|
Depuis l'Antiquité, on sait calculer l'aire
des figures simples (carrés,
triangles,
et même cercle).
Les Grecs
cherchaient à connaitre précisément l'aire des sections coniques:
parabole, ellipse et hyperboles et n'y parvenaient pas. Archimède a su calculer l'aire du disque était
compris entre 3 + 10/71 = 3,140... et 3 + 1/70 = 3,142 (deux décimales de
Pi). Il a aussi montré que l'aire d'un segment de parabole est égale à quatre
tiers fois l'aire du triangle inscrit dans ce segment. Au XVIe
siècle, Simon Stévin (1548-1620) et François Viète (1540-1603) utilisent des
additions d'une infinité de nombres. Mais, la détermination de l'aire reste
problématique. Descartes
(1596-1650) invente la géométrie analytique, introduisant les équations des
courbes. Pas encore suffisant. Le calcul
intégral, qui s'est développé au XVIIe siècle avec les travaux de Bonavantura
Cavalieri, Isaac Newton, Leibniz... >>> |
![]()
|
Anglais |
Calculus is the great Mount Everest of math. Most of the world is content
to just gaze upward at it in awe. But only a few brave souls attempt the
ascent. Or maybe not. L'analyse est le mont Everest des maths. La plupart des gens se
contentent de l'admirer d'en bas. Mais, seuls quelques courageux tentent
l'ascension, ou pas. |
![]()
Primitive des fonctions simples
|
Fonction |
Fonction primitive |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Voir Table des primitives
de ce type de fonctions
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exemples simples de calcul d'une intégrale
Reconnaissance de la primitive et calcul de la différence
pour les deux bornes
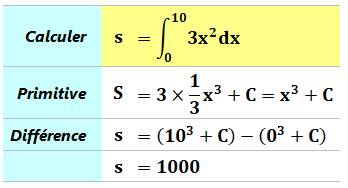
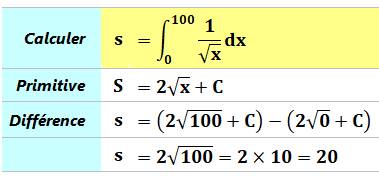
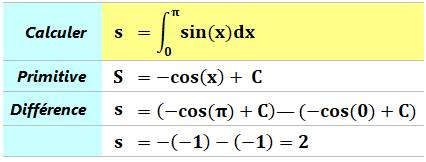
Voir Brève 57-1130
![]()
Règles d'intégration
|
|
|
|
|
|
|
Exemple
|
|
|
Exemple
|
|
|
Exception
|
|
|
|
|
|
Exemple
|
|
![]()
|
En savoir plus |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosP/Primitiv.htm
|
![]()