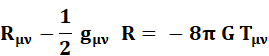|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
RELATIVITÉ
GÉNÉRALE
|
|
Satellite Microscope (Microsatellite à traînée
compensée pour l’observation du principe d’équivalence): mis sur orbite
héliosynchrone en 2016. But: vérifier le principe d'équivalence, un des postulats
de la relativité générale. Autrement-dit: vérifier que les corps tombent dans le vide
avec exactement la même accélération. En 2018: mesures sur 1 900 orbites soit un équivalent
de 85 millions de kilomètres de chute libre. Confirme l'exactitude avec 2 10-14 de précision Suite: atteindre une précision de quinze décimales. |
Voir Chute des corps
Janvier 2016 – Conjecture de la courbure L2**
|
Conjecture
émise en 2000 et résolue en 2016 par trois chercheurs >>> La théorie de la gravitation
(relativité générale) stipule que la matière
courbe l'espace-temps avec un effet d'autant plus fort que la masse de
l'objet est importante. Les mathématiciens caractérisent cette courbure par un tenseur (sorte de
super-vecteur) qui intervient dans les équations
de la relativité. Selon la conjecture,
il existe une solution si, à l'instant initial, l'intégrale du carré du tenseur est un nombre
fini. La conjecture de la courbure L2 est impliquée également
dans la démonstration des conjectures de censure cosmique de Penrose relatives aux
singularités gravitationnelles (comme les trous noirs). |
Voir Conjecture / Actualité 2016
![]()
|
|
||
|
On s'intéresse au domaine des |
vitesses qui varient. |
|
|
C'est-à-dire les |
mouvements accélérés. |
|
|
La formule de la gravitation est connue (Newton) |
F = G.m.m' / d² |
|
|
Explication (Einstein): |
L'univers est courbé par l'effet des objets. |
|
|
La gravitation est |
la distorsion de l'espace et du temps. |
|
|
En l'absence de toute masse, la structure espace-temps est |
plate. |
|
|
et, un objet peut |
-
rester au repos, ou -
cheminer à vitesse constante. |
|
|
Arrive une masse |
l'espace se courbe. |
|
|
La déformation n'est pas instantanée, elle se propage |
à la vitesse de la
lumière. |
|
|
Il y a équivalence entre |
-
gravitation et -
accélération. |
|
|
Une situation en mouvement accéléré admet une description équivalente |
-
sans accélération, mais -
avec gravitation. |
|
|
|
|
|
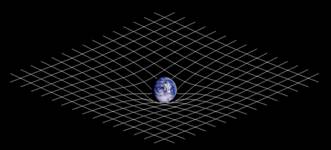
Une image est souvent utilisée pour se
représenter l'effet de la déformation. Elle consiste à montrer l'espace comme une
toile de trampoline. Attention: L'analogie simplifie le nombre de
dimensions. La toile est plate en l'absence de tout
objet. Un objet massif la déforme en la creusant
Dans ces conditions, un nouvel objet lancé
sur cette toile sera dévié de sa trajectoire naturelle s'il passe à proximité
de l'objet massif. Ce sera une simple déformation de la trajectoire (comme
figuré ci-dessus) Ou même, l'objet sera piégé et se mettra à
tourner dans la cuvette créée par l'objet massif à la manière d'une bille
lancée dans un bol. C'est le cas des planètes
autour du soleil Note Il faut remarquer que le nouvel objet en
mouvement, lui aussi, crée une déformation dans la toile, déformation qui se
propage autour de lui à la vitesse de la lumière. Attention L'image de la toile de trampoline est
incorrecte. Notamment il manque une dimension. Tout comme l'est l'image de l'électron qui
tourne autour du noyau, à la manière d'un système planétaire. Il faut le savoir lorsqu'on entre plus
profondément dans ces théories. Mais pourtant, que c'est pratique de se
raccrocher à quelque chose que l'on peut visualiser! Un des défauts, facile à comprendre, mais
très subtil: Dans l'analogie, la toile du trampoline se
déforme sous l'effet de la gravité. Or, dans la réalité la distorsion de
l'espace, c'est LA GRAVITÉ elle-même. |
|
Voir Effet de fronde
|
|
|
|
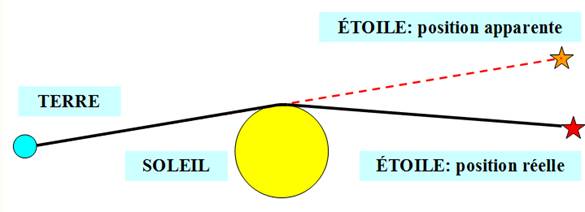
Visualisons la trajectoire de l'objet qui
traverse le trampoline ci-dessus en imaginant que l'objet massif est le Soleil et que la trajectoire représente celle de
la lumière d'une étoile.
Vue de la Terre, l'étoile semble en face,
alors qu'en réalité sa lumière a été déviée par le Soleil. C'est la base de
l'observation faite lors de l'éclipse de 1919 qui
a prouvé la justesse de la théorie de la relativité générale. |
|
|
|
||
|
Deux énoncés clés qui résument la relativité générale. |
La trajectoire
d'un corps dans un champ gravitationnel prend la forme d'une géodésique de
l'espace tétradimensionnel (espace-temps). La relation
entre la présence de la masse et la forme de l'espace tétradimensionnel est
représentée par l'équation suivante:
|
|
|
Traduction de cette formule. |
"L'espace dit
à la matière comment elle doit se déplacer, et la matière dit à l'espace
comment il doit s'incurver" – Wheeler En gros: la courbure (R) est proportionnelle à
un nombre G (gravitation) et à la quantité de matière ou d'énergie présentes
(T). |
|
D'après
L'espace est une question de temps – Einstein et la relativité – David Blanco Laserna – Les grandes idées de la science – 2013
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()