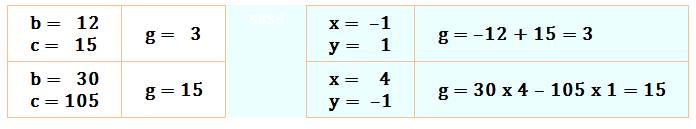NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/10/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Théorie des Nombres
Débutants Division	DIVISIBILITÉ			Glossaire Division
INDEX Accueil Sommaire	Approche	Divisible	Division
		Div. commun	Applications
		Sommaire de cette page >>> Diviseur commun >>> Définition du PGCD >>> Expression linéaire >>> Démonstration >>> Identité de Bézout >>> Lemme d'Euclide >>> Propriété 1 >>> Premiers entre eux >>> Propriété 2 >>> Divers

DIVISEURS communs ou non

PGCD: plus grand commun diviseur.

PPCM: plus petit commun multiple.

Un peu de théorie, utile pour étudier les propriétés des nombres premiers entre eux.

Notations: on ne sait jamais où les chercher !

a divise b	PGCD de (a, b)	PPCM de (a, b)
ab	(a, b)	[a, b]

Personnellement, je conserve le point pour signifier multiplication: a . b

Beaucoup d'ouvrages l'omettent: ab

Pour se rafraîchir la mémoire, voir Nombres un peu divisibles entre eux

DIVISEUR COMMUN
Diviseur commun de deux nombres
si a divise b et a divise c	a est un diviseur commun de b et c.
3 divise 12 3 divise 30	3 est un diviseur commun de 12 et 30.
6 divise 12 6 divise 30	6 est un diviseur commun de 12 et 30.
La quantité de diviseurs de b est limitée La quantité de diviseurs de c est limitée	La quantité de diviseurs communs de b et c est limitée. Il en existe un qui est le plus grand. C'est le Plus Grand Commun Diviseur: PGCD
6 divise 12 6 divise 30	6 est un diviseur commun de 12 et 30. C'est le plus grand !
Diviseur commun de plusieurs nombres
si a divise b1 et a divise b2 et a divise b3 … et a divise bi	a est un diviseur commun de b1 , b2 , b3 … bi
3 divise 6 3 divise 99 3 divise 123 3 divise 1236	PGCD (6, 99, 123, 1236) = 3 Il est le plus petit, car le second diviseur de 6 est 2 et 99, impair, n'est pas divisible par 2.
Notations	PGCD ( b1 , b2 , b3 … bi ) g ( b1 , b2 , b3 … bi ) ( b1 , b2 , b3 … bi ) g

Définition du PGCD
Soit b et c Z tels que b.c 0. Le PGCD de b et c est l'entier positif g qui satisfait aux deux conditions suivantes:	i) g b et g c g divise à la fois b et c ii) si m b et mb, alors m g S'il existe un autre diviseur commun, il est plus petit que g; c'est g le plus grand.
Given any two integers b and c, not both zero, there is a unique positive integer g, called their greatest common divisor, with these properties:	i) g b and g c ii) if m b and m b, then m g

Voir Calcul du PGCD

Théorème
Si g est le PGCD de b et c, alors, il existe deux entiers u et v tels que l'expression linéaire g = b.x + c.y soit satisfaite. Et, même, le PGCD de deux nombres est la plus petite valeur positive de l'expression b.u + c.v u et v sont d'ailleurs premiers entre eux.	g = (b , c) g = b.u + c.v Cette relation est naturellement généralisable à plus de deux termes.
Exemple

Démonstration
Constat pour lancer la démonstration
Soit la combinaison linéaire:	E	= b.x + c.y
Pour x et y valant 0, elle vaut 0. Selon les valeurs de x et y, elle sera positive ou négative.	E	= 0 < 0 > 0
Autrement dit, il existe une valeur positive, la plus petite pour xp et yp.	Ep	= b.xp + c.yp
Principe de la démonstration
E est la plus petite valeur positive. Si E est le PGCD recherché, E divise b et c.	Ep Ep	b c
On procède par l'absurde, en supposant que E ne divise pas b. On fera de même pour c. On cherche la contradiction, prouvant que l'hypothèse est fausse.	Hypothèse: Ep	ne divise pas b
Recherche de la contradiction
Selon la définition de la division. Avec l'inégalité importante: r est inférieur à E.	b 0 < r	= q.Ep + r < Ep
Exprimons r , en reprenant ce que nous avons trouvé pour plus petite valeur de E, candidate au PGCD. Expression linéaire de la forme de celle du départ	r	= b – q.Ep = b – q (b.xp + c.yp) = b(1 – q.xp) + c(-q.yp) = b . X + c . Y
Mise en évidence de la contradiction
Récapitulons: r fait partie des valeurs de E du départ. Or, r est une valeur inférieure à Ep	r r	= b . X + c . Y < Ep
Or nous avons justement choisi Ep la plus petite valeur de E Il ne peut pas exister plus petit	Contradiction! Ep	est bien un diviseur de b et c
Comparaison avec g
Si g est le PGCD de b et c	b c	= g . B = g . C
En exprimant Ep	Ep	= b.xp + c.yp = g.B.xp + g.C.yp = g (B.xp + C.yp)
Il est possible de conclure que g divise Ep Ce qui veut dire que g est inférieur ou égal à Ep	g g	Ep Ep
Or Ep et g sont des diviseurs de b et c g est le plus petit Ep ne peut pas être encore plus petit et Ep = g	Ep = g	= b.xp + c.yp

Application: Résolution d'équations diophantiennes
Équation:	a.u + b.v	= c
Solution si PGCD de a et b (g) divise c.	g	c
Autrement-dit:	a.u + b.v	= k . g
S'il y a une solution (u, v), alors, il y a une infinité (U, V) selon la valeur du paramètre t.	U V	= u + t . b / g = v – t . a / g

Voir Équation linéaire en ax +by = c / Équations diophantiennes

Identité de Bézout Application directe de l'expression linéaire trouvée ci-dessus
g = (a, b)	Avec g le PGCD de a et b
a. u + b. v = g a' = a / g b' = b / g a'. u + b'. v = 1	Si cette relation existe, b et c sont divisés par leur plus grand diviseur g. b' et c' sont donc premiers entre eux. L'expression linéaire est égale à 1. C'est une propriété des nombres premiers entre eux. C'est même une condition nécessaire et suffisante pour que deux nombres soient premiers entre eux.
(a', b') = 1	Les nombres a' et b' sont premiers entre eux.

Voir Identité de Bachet - Bézout / Identités spéciales / Application / Petit théorème de Bézout / Équations

Démonstration du lemme d'Euclide-Gauss avec Bézout
Lemme d'Euclide	Si (a, b) = 1 Si a b.c	alors a c
Identité de Bézout	(a, b) = 1	a.u + b.v = 1
En multipliant par c	c	= a.c.u + b.c.v
Or a divise un produit en a Et par hypothèse divise le produit b.c	a a	a.c.u b.c.v
Il divise les deux termes de la somme, il divise la somme Qui vaut c.	a a	a.c.u + b.c.v c

Voir Familiarisation avec la divisibilité / Application du lemme d'Euclide au binôme

PROPRIÉTÉ 1
Pour tout nombre positif m le PGCD des produits m . a et m . b est égal à m fois le PGCD de a et b.	(m.a, m.b)	= m (a, b)
Démonstration Appliquons le théorème précédent	(m.a, m.b)	= (m.a.u + m.b.v)plus petit = m (a.u + b.v)plus petit = m (a, b)
Application: premiers entre eux Si d divise a et b	d d	a b
Application du théorème en remplaçant m, a, b par d, a/d, b/d
Cas où d est le PCGD = g = (a, b)
Cas où les deux nombres sont premiers entre eux: g = 1	(a , b )	= 1

PREMIERS ENTRE EUX – Définitions
Si le PGCD de deux nombres est égal à 1, ces deux nombres sont premiers entre eux, on dit aussi "étrangers" (ou encore copremier, coprime, relatively prime en anglais) Dans ce cas, il existe une expression telle que:	(a, b) = 1 a.x + b.y = 1
Si le PGCD de plusieurs nombres est égal à 1, ces nombres sont premiers entre eux, on dit aussi "étrangers" Dans ce cas, il existe une expression telle que:	(a, b, c … i) = 1 a.x + b.y + c.z + … i.j = 1
Si le PGCD de plusieurs nombres pris deux à deux est égal à 1, ces nombres sont premiers entre eux deux à deux, on dit aussi "étrangers par paires"	(ai , bj) = 1

Suite Premiers entre eux

PROPRIÉTÉ 2
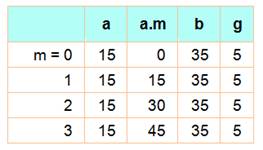
Pour tout entier m, le PGCD de a et a.m + b est égal au PGCD des deux nombres a et b de départ.	(a, b) = (a, a.m + b)
Exemple
Démonstration Soit les PGCD suivants avec leur expression linéaire. Il s'agit de monter qu'ils sont égaux.	d g	= (a, b) = a.u + b.v = (a, a.m + b) = a.U + (a.m + b)V
d divise a, b et aussi un multiple de a: a.m Il faut démonter que g = d	d est un diviseur commun de (a et a.m + b) g est le plus grand (notre hypothèse) d g
Prenons l'expression de d. Et introduisons la quantité a.m.v en plus et en moins.	d	= a.u + b.v = a.u – a.m.v + a.m.v + b.v = a (u – m.v) + (a.m + b).v = a. U' + (a.m + b) V'
Cette expression en U' et V' est du même type que celle exprimant g. Or celle en g est telle que g (le PGCD) est la plus petite des solutions d'une telle relation.	d g d	= a. U' + (a.m + b) V' = a. U + (a.m + b) V g
d plus grand et plus petit est en fait égal à g.	d	= g

Application: recherche du PGCD, et de x, y par l'algorithme d'Euclide
Écrivons la division de b par c.	b r	= c.q + r = b – c.q
En appliquant notre nouveau théorème:	(b, c)	= (b – c.q, c)
Ou encore:	(b, c)	= (r, c)
Le PGCD de deux nombres est égal à celui de l'un deux et du reste de la division de l'autre par l'un.
Exemple
Soit: 85 et 15	(85, 15)	= 5
Formulons la division; elle donne 10 pour reste.	85	= 3 x 15 + 10
Le reste avec le dividende donne le même PGCD.	(10, 15)	= 5

DIVERSES PROPRIÉTÉS des PGCD
Cas simple	(a, a + 2)	= 1 si a impair = 2 si a pair
Cas plus complexe!	(a^2^m + 1, a^2^n + 1) a, m, n > 0 et m ≠ 0	= 1 si a est pair = 2 si a est impair
Carrés	(a, b) = c (a, b) = (a, c)	(a², b²) = c² (a², b²) = (a², c²)
Étrangers	(a, b) = a.x + b.y	(x, y) = 1
Étrangers	Si (a, b) = 1	(a + b, a – b) = 1 ou 2 (2a + b, a + 2b) = 1 ou 3 (a² + b², a + b) = 1 ou 2 (a + b, a² – a.b + b²) = 1 ou 3 (a + b, a² – 3a.b + b²) = 1 ou 5 (a + b , (a^p + b^p) / (a + b)) = 1 ou p (p>2)
Factorielles	{ n! +1, (n+1)! + 1 }	= 1
Transitivité	(a, b) = (a, c) (a, b.c) = 1	(a, b) = (a, b, c) (a, b) = (a, c) = 1
Associativité	(a, b, c)	= { (a, b) , c }
Distributivité	(b, c) = 1	(a, b.c) = (a, b) (a, c) (b.x + c.y, b.c) = (b, y) (c, x)
Combinaison linéaire	(a, b)	= (a, b, a + b) = (a, b, ax + by)
Divisibilité	(b, c) = 1 et b a et c a	bc a
	(a, a + k)	k
	a b.c	{ a / (a, b) } c

Bilan

Nous avons complété nos connaissances sur les propriétés de divisibilité entre plusieurs nombres.

Le PGCD est exprimable par une fonction linéaire.

Lorsque les nombres sont étrangers (premiers entre eux), le PGCD est égal à 1, de même que l'expression linéaire.

Comment trouver le PGCD et l'expression linéaire? C'est l'objet de la prochaine page …

Suite	PGCD et algorithme d'Euclide PPCM Facteurs et diviseurs Algorithme d'Euclide Équation linéaire en ax +by = c
Autour	La division en pratique c'est quoi? – Débutant La division en résumé c'est quoi? – Glossaire Lemmes d'Euclide, de Gauss Divisibilité par un nombre donné
Voir	Cryptage Des jeux sur les partages Jeux et puzzles – Index L'arithmétique de l'horloger Le calcul mental Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Referenc/Prof/APROF/DivCommu.htm