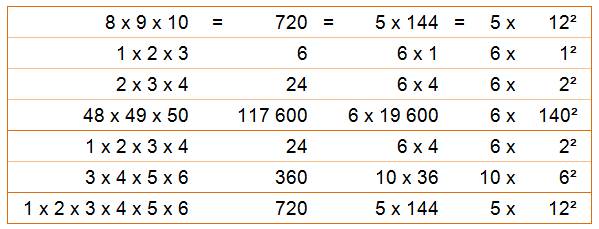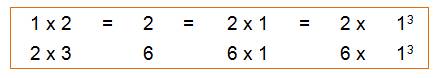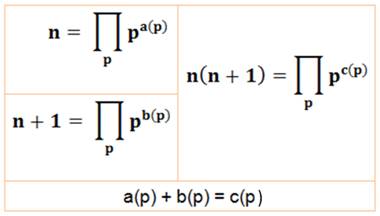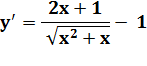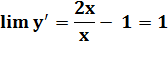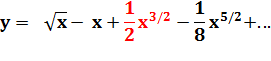|
|||||||||||||||||||||||||||
![]()
|
NOMBRES CONSÉCUTIFS Produit =
Carré ? Puissance ? Un
produit de nombres consécutifs comme 3x4x5 est une factorielle tronquée. En
1724, Christian Goldbach
démontre que le produit de
trois nombres consécutifs n'est jamais un carré:
(n – 1) n (n + 1) C'est vrai également pour deux consécutifs seulement: n (n + 1) |
Voir Expression
littérale des produits de consécutifs
|
Je
ne me souviens plus du carré de 7; J'hésite! prendre
les deux nombres autour de 7, les multiplier et ajoutez 1. 7² = 6 x 8 + 1 = 48 + 1 = 49 n² = (n – 1) (n + 1) + 1 |
Voir Calcul
des carrés
|
|
||
|
Le produit de n (>1) nombres consécutifs n'est
jamais une puissance. Démontré par Erdös et Selfridge |
Théorème (n + 1) (n + 2) … (n + k) = xh n'a pas de solution n |
|
|
Historique
|
Cas des carrés (n + 1) (n+2) … (n + k) |
|
|
Le produit de n (>1) nombres consécutifs est
rarement M fois une puissance, sauf pour k = 2 |
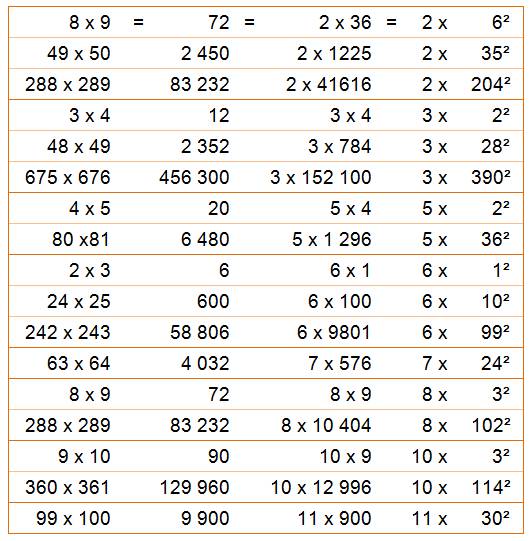
Exemples Deux consécutifs (k = 2), au carré (h = 2) et deux fois (M = 2): 8 x 9 = 2 x 6² Trois consécutifs, carré et M = 5: 8 x 9 x 10 = 5 x 12² = 20 x 6² |
|
![]()
|
|
||
|
Deux nombres consécutifs
Deux nombres NON consécutifs
Trois nombres consécutifs
|
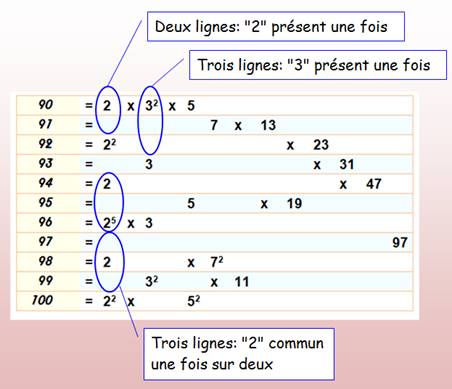
Sur deux lignes successives: aucun facteur en
commun. Le facteur "2" est toujours présent une seule fois. Sur trois lignes successives: le facteur
"2" est commun une fois sur deux. Aucun autre facteur en commun. Le
"3" est toujours présent une seule fois. |
|
|
Dans une suite de nombres consécutifs, il n'y a pas de facteur commun. Dans une telle suite, tous
les couples de consécutifs sont premiers entre eux. Comme le zéro qui annule
un produit, ces couples annulent la possibilité de facteurs communs pour
l'ensemble de la suite. En effet: Si A = PGCD (a,
b), alors PGCD (a, b, c) = PGCD (A, c) Si A = 1 alors
PGCD (a, b, c) = PGCD (1, c) = 1 |
||
|
|
||
|
Théorème Le produit de deux nombres consécutifs n'est jamais un carré. La démonstration fait intervenir la
somme des exposants de la décomposition
en facteurs premiers. Démonstration pour N =
n (n + 1) Naturellement n et n + 1 sont premiers entre eux: aucun facteur en
commun. Or si N = n (n + 1) est un carré
tous les exposants (c(p)) sont en 2k. Alors, tous les exposants de n et de
n + 1 (a(p et b(p)) devraient être pairs. Ce qui
impliquerait que n et n + 1 seraient eux-mêmes des carrés. Ce n'est pas le
cas. |
Factorisation première
des nombres
Illustration de la
démonstration
|
|
|
|
||
|
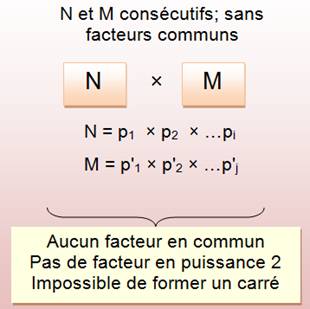
Théorème Le produit de k nombres consécutifs n'est jamais un carré. Démonstration pour N =
(n – 1) n (n + 1) Deux cas se présentent:
Pour k nombres consécutifs Tous ces nombres étant premiers
entre eux, il est impossible d'obtenir un exposant en 2k pour chacun des
facteurs formant le produit. Impossible de former un carré. |
Produits avec racine
proche d'un entier (exemples)
Produits proches de
consécutifs avec racine entière Triviaux du fait de la présence d'un
carré 4 x 5
x 5 = 100 = 10² 8 x 9
x 8 = 576 = 24² 9 x 10
x 10 = 900 = 30² Triviaux
du fait d'un nombre produit des précédents 2 x 3
x 6 = 36 = 6² 3 x 4
x 12 = 144 = 12² Originaux
avec carrés cachés 2
x 3 x 4 x 6 = (2x6) x (3x4) = 144 = 12² 2
x 3 x 4 x 5 x 5 x 6 = 3600 = 60² 7 x 8 x 14 = 784 = 28² 21 x 27 x 28 = 15 876 = 126² 7 x 8 x 9 x 14 = 7056 = 84² 48 x 49 x 50 x 54 = 6350400 = 2520² 88 x 98 x 99 x 100 = 85377600 =
9240² |
|
|
Racine du produit de deux
consécutifs** ** Calculs avancés |
|
|
|
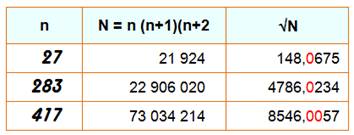
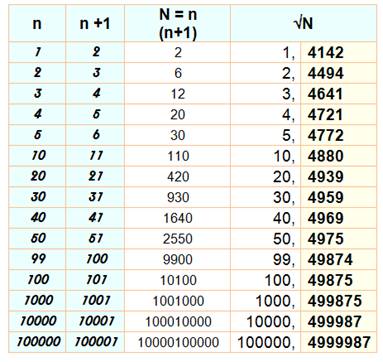
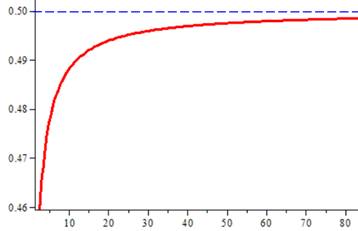
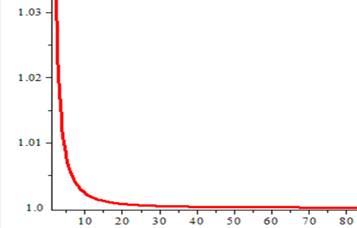
Observations Nous allons expliquer une curiosité: Soit la racine du produit de deux nombres consécutifs. Sa partie
fractionnaire tend vers 0,5 lorsque n croît. Le tableau comme le graphe montre
une rapide croissance vers l'asymptote. Nous confirmons également que le
produit a peu de chance d'engendrer un carré! Explications Les deux nombres consécutifs: n et n
+ 1 Le produit comparé au carré du
premier: n (n + 1) – n² = n² + n – n² = n Ex: 5
x 6 – 5² = 5 Passons à la racine en baptisant les
nombres x et x + 1 (habitude pour le traitement des fonctions). L'écart de la
racine du produit au nombre initial (x) vaut:
Sa dérivée:
Tendance pour x très grand (x petit
devant x²):
Lorsque x est grand la nouvelle
valeur de y est multipliée par 1,00 …+ et tend vers une valeur
asymptotique égale à 0,5. Cette valeur
limite n'est pas évidente à calculer analytiquement. Le développement en
série de y donne:
C'est le coefficient du monôme de
plus fort degré qui l'emporte lorsque x croît. |
Tableau de convergence
de la partie fractionnaire de racine de N
Graphe de y
Graphe de la dérivée
y'
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()