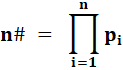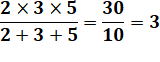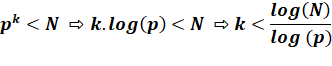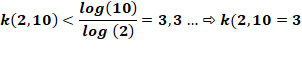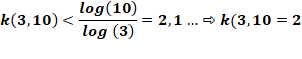|
||||||||||||||||||||||||||||
![]()
|
PRIMORIELLES Produit des nombres premiers & Super-primorielles Les primorielles sont construites comme les
factorielles, mais en ne retenant que les nombres premiers successifs. Elle est
notée n#. Par exemple 5# = 2 x 3 x 5 = 30 (premiers jusqu'à 5)
ou aussi 5# = 2 x 3 x 5 x 7 x 11 = 2 310 (cinq premiers). Nom donné par Harvey Dubner. Les super-primorielles
sont une extension des primorielles avec facteurs premiers portés à une
puissance particulière. |
Voir Somme
des nombres premiers
Anglais - Primorial
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Définition Produit des nombres premiers
successifs jusqu'à n, n compris s'il est premier. Noté n# ou, parfois
P(n).
Exemples P(5) = 5# = 1 x 2 x 3 x 5 = 30 P(6) = 6# = 1 x 2 x 3 x 5 = 30 P(7) = 7# = 1 x 2 x 3 x 5 x 7= 210 P(8) = 8# = 1 x 2 x 3 x 5 x 7= 210 Valeurs
successives
Moyenne
selon les plages
|
|||||||||||||||||||||||||||||||||||||||||
Voir Table – Index
/ Primorielle 29
|
|
|||
|
|
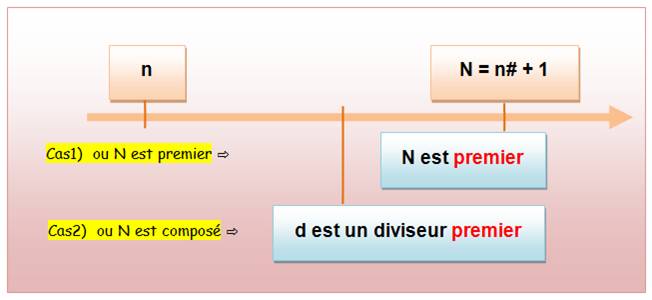
n le plus grand des premiers |
||
|
Deux cas possibles
=> |
N = n# + 1 N premier ou pas |
||
|
Liste des
nombres d'Euclide E = n# + 1 |
2,
3, 7, 31, 211, 2311, 30031,
510511, 9699691, 223092871, 6469693231, 200560490131,
7420738134811, 304250263527211, … OEIS A006862 En rouge,
les nombres d'Euclide premiers. |
||
|
Cas 1) – Supposons N premier.
|
N > n N serait un premier encore plus grand que n |
||
|
Cas 2) – Supposons N composé.
il divise n#
et n!! +1 Il divise 1. Rappel: la barre
verticale veut dire "divise".
|
N = … x d x … d < n n# = … x d x … d d d d |
||
|
|
n le plus grand des premiers: FAUX Infinité
de premiers. |
||
Voir Infinité
de nombres premiers / Nombres
d'Euclide = n# + 1
Nombres fortunés – Nommés d'après Reo Fortune(1903-1979)
|
Nombres
Fortuné:
F = Premier – Primorielle Primorielle:
produit des n premiers nombres premiers. Premier:
celui juste supérieur à la primorielle, écart supérieur à 1. Fortune
conjecture que ces nombres sont toujours premiers. EN 2020, tous les nombres
fortuné connus sont effectivement premiers, mais la conjecture n'est pas
démontrée. Premières
valeurs: Primorielle, premier, Fortuné 1, 3, 2 2, 5, 3 6, 11, 5 30, 37, 7 210, 223,
13 2310,
2333, 23 30030,
30047, 17 510510,
510529, 19 9699690,
9699713, 23 223092870,
223092907, 37 6469693230,
6469693291, 61 200560490130,
200560490197, 67 7420738134810,
7420738134871, 61 304250263527210,
304250263527281, 71 Liste
selon rang: 3, 5, 7,
13, 23, 17, 19, 23, 37, 61, 67, 61, 71, 47, 107, 59, 61, 109, 89, 103, 79, 151,
197, 101, 103, 233, 223, 127, 223, 191, 163, 229, 643, 239, 157, 167, 439,
239, 199, 191, 199, 383, 233, 751, 313, 773, 607, 313, 383, 293, 443, 331,
283, 277, 271, 401, 307, 331, ... OEIS A005235 Liste
selon valeur: 3, 5, 7,
13, 17, 19, 23, 37, 47, 59, 61, 67, 71, 79, 89, 101, 103, 107, 109, 127, 151,
157, 163, 167, 191, 197, 199, 223, 229, 233, 239, 271, 277, 283, 293, 307,
311, 313, 331, 353, 373, 379, 383, 397, 401, 409, 419, 421, 439, 443, 457,
461, 491, 499, 509, …. OEIS
A046066 |
|
|
|||
|
Exploitation
de la propriété concernant le PGCD
d'une primorielle (2x3x5 …p) avec un nombre (n) plus grand que p. |
Alors, le plus petit nombre n avec PGCD = 1 est un nombre premier. PGCD(10, 30) = 10 => 10 est composé PGCD(11, 30) = 1 => 11 est premier. |
||
|
Pour
accélérer la recherche, seuls les nombres en 6k |
En effet, tous les nombres premiers
sont de la forme p = 6k |
||
|
|
Commentaires On commence en traitant séparément le cas des
nombres 2 et 3 mis dans une liste (L) et on compose la première primorielle
Prim. Boucle qui commence à 6 et qui progresse de 6 en
6 (by 6). Traitement du cas 6k – 1. Si le PGCD (gcd en anglais) est égal à 1, on
complète la liste L. Traitement du cas 6k + 1. Si le PGCD (gcd en anglais) est égal à 1, on
complète la liste L. Après avoir indiqué la fin de la boucle (od, le
do à l'envers), impression de la liste. En bleu, la liste calculée en un temps nettement
plus rapide que l'application du crible d'Ératosthène. Note: programme peu
malin car le calcul du PGCD, inclus dans le logiciel Maple, est lui-même basé sur la
connaissance des nombres premiers. ALORS? Comment se passer du PGCD? Utiliser les super-primorielles! |
||
Voir Programmation – Index
|
|
|
|
Petit dessin pour situer les nombres
premiers tels que montrés dans la démonstration:
Ce dessin illustre le fait qu'il
existe toujours un nombre premier entre n et N
= n# + 1 (primorielle). Avec une démonstration du même type, on
peut montrer qu'il
existe toujours un nombre premier entre n et N = n! + 1 (factorielle). L'intervalle avec la primorielle
(nombres premiers) est plus petit que celui avec factorielle (tous les
nombres). |
|
|
|
|
|
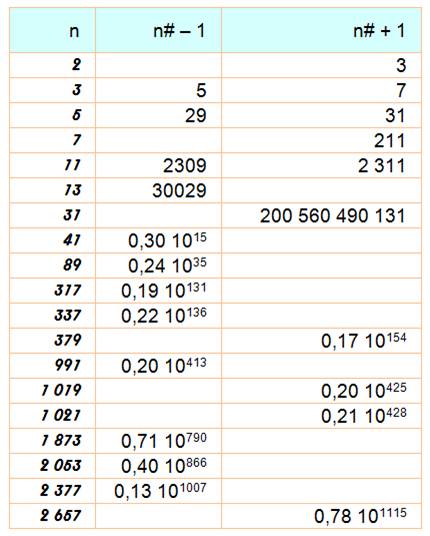
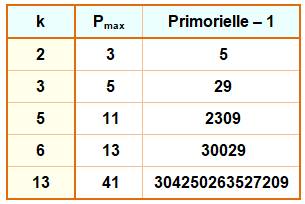
Comme pour les factorielles,
on se pose la question de savoir si les primorielles plus
un ou moins un sont des nombres premiers. Liste des primorielles
premières jusqu'à 3000
Primorielle première –
1 ou Primorial -1 primes
|
|
|
|
||
|
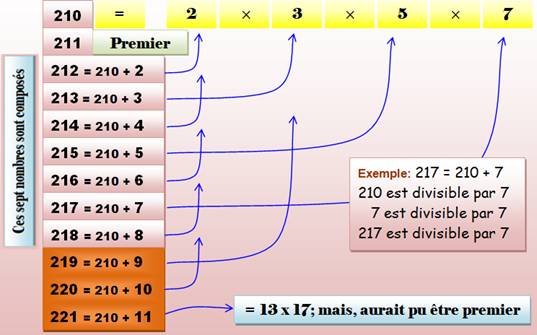
Comme pour les factorielles, les
primorielles sont suivies d'une quantité minimale de nombres composés. En omettant le suivant (+1)
qui peut être premier, les p suivants sont composés.
|
Exemple avec
primorielle 7 = 210
Note: 222 = 2
x 3 x 37 ; 223 est premier; |
|
|
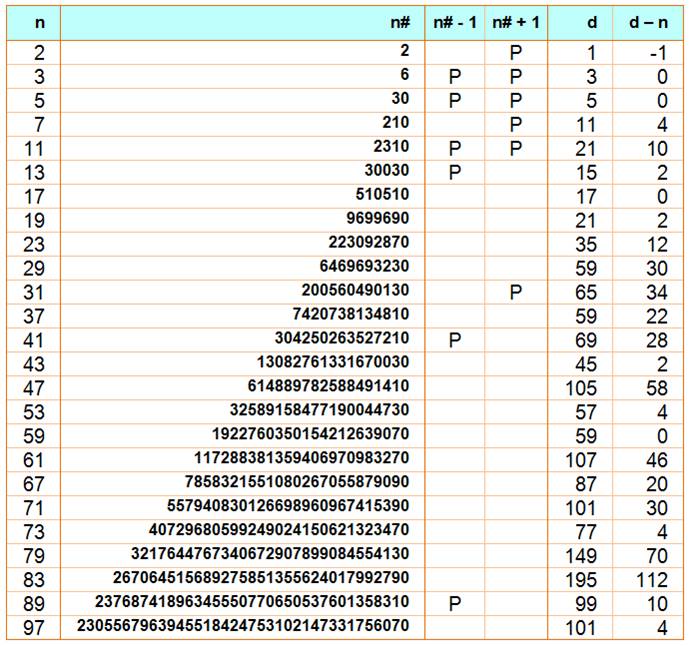
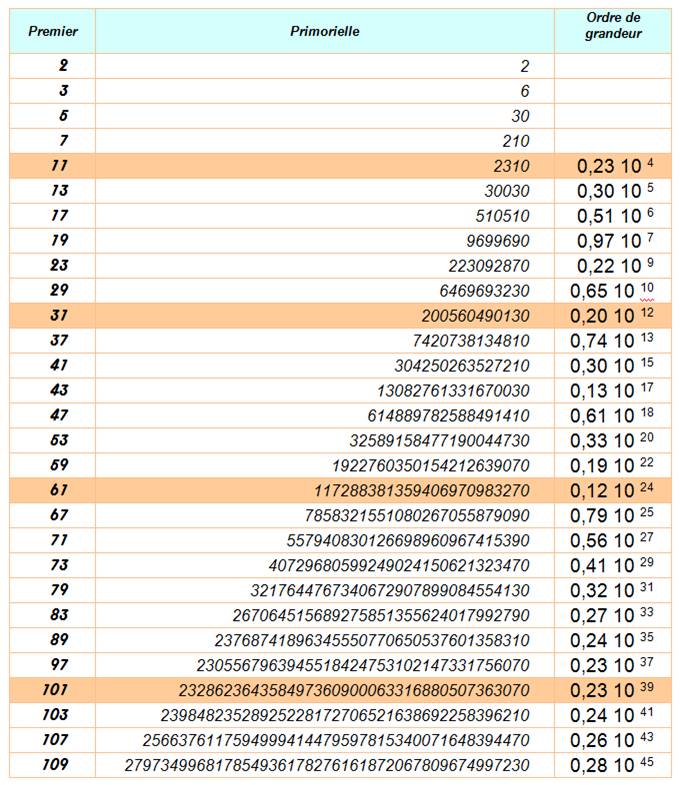
Plage de nombres
composés derrière une primorielle Ce
tableau donne la quantité d de nombres
composés qui suivent le nombre n# + 1.
Il est toujours égal ou plus grand que n (sauf pour 2). L'excédent d – n tend
à croître avec n, mais souffre d'exceptions, comme avec 59#.
|
||
Merci à Louis F. pour
ses judicieuses remarques
![]()
Une certaine manière de voir la notion de Plus Petit Commun Multiple
des nombres de 1 à N
|
Super-primorielles ou PPCM
(1..N) |
|
|
|
Définition La
super-primorielle d'un nombre N est une primorielle dont les facteurs
premiers sont portés à une certaine puissance
en rapport avec N. En fait,
parmi les facteurs de la super-primorielle de N, on compte toutes les puissances des facteurs premiers inférieures à N. |
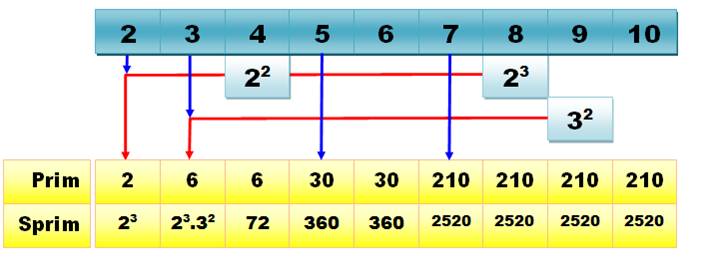
SP(N) = 2a . 3b . 5c . 7d
. … Avec 2a < N et 2a+1 >N 3b < N
et 3b+1 >N Etc. Exemple SP(10) = 23 . 32 . 5 . 7 = 2 520 Car on trouve (2, 22, 23) et (3 et 32) jusqu'à 10. En fait: SP(10) = PPCM (1, 2, 3, 4, 5, 6,
7, 8, 9, 10) |
|
|
Exemple pour N = 10, la
super-primorielle vaut 2 520 La super-primorielle contient toutes les
puissances des nombres premiers inférieures à un nombre donné N.
|
||
|
Calcul Comment déterminer
la puissance maximale de chaque facteur premier. Un nombre
premier (p) à la puissance k doit être inférieur à N. Le
passage aux logarithmes permet le calcul
de l'exposant. La puissance à retenir est l'entier obtenu en ignorant la
partie décimale. |
Exemple
|
|
|
Propriété La
super-primorielle offre un avantage sur la primorielle simple en termes de divisibilité. Autre définition de la
super-primorielle de N: nombre divisible par tous les
nombres qui sont inférieurs à N, ce qui est la définition du plus petit
commun multiple (PPCM) de tous les
nombres de 1 à N. |
La super-primorielle de N est divisible par tous les nombres
inférieurs à N. Exemple SP(10) = 2 520 est divisible par 8, car 23 est l'un des
facteurs; de même, il est divisible par 9, car 32 est l'un des
facteurs. |
|
Merci à Didier T.
Table des super-primorielles jusqu'à N = 50
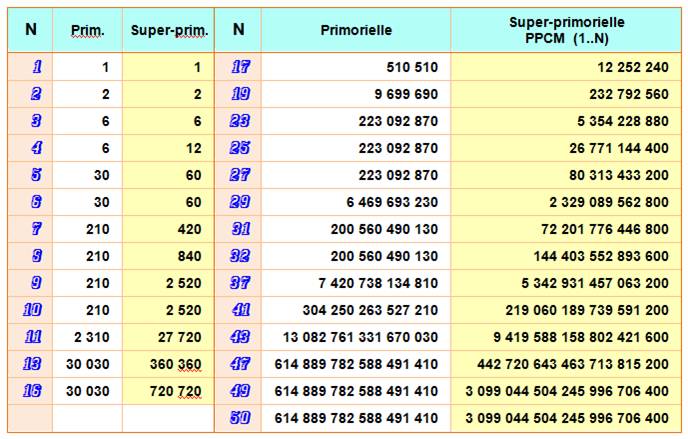
Voir Table – Index
Idée d'un algorithme de
recherche des nombres premiers
|
Yves Roques est l'auteur d'un algorithme de recherche
des nombres premiers qui exploite la propriété des super-primorielles. Pour
une étendue de recherche jusqu'à N, l'idée consiste à construire la
super-primorielle de N au fur et à mesure de la détection des nombres
premiers. La super-primorielle y est nommée: NEA = Nombre Entier Atomique.
Voir cette vidéo
>>> |
Le chapitre ci-dessous reprend les travaux d'Yves Roques et
ajoute une variante
|
Application: recherche de nombres
premiers Le programme Maple vu ci-dessus peut être amélioré en
s'affranchissant du calcul du PGCD. Il est remplacé par une division, ou
plutôt un calcul modulo, testant
simplement la divisibilité. |
Ce qu'il faut comprendre: le programme sait reconnaitre les nombres
premiers, mais une fois la primorielle
calculée, les nombres premiers antérieurs sont enfouis. Ils ne sont plus
accessibles. D'où l'idée d'en faire usage complètement dès qu'ils se
présentent, et ceci, en calculant la super-primorielle. |
|
Programmation Après réinitialisation, mise à 1 de la
super-primorielle et spécification de la limite de calcul (N = 10) Lancement d'une boucle d'exploration des nombres
de 2 à N. Si la super-primorielle n'est pas divisible
par le nombre en cours d'exploration,
alors il s'agit d'un nouveau nombre
premier. Cette puissance avec cet exposant est introduite
dans la super- primorielle. Impression de i, la nouvelle puissance. Ici, on a
aussi imprimé quelques paramètres supplémentaires pour information. |
|
|
Accélération de l'exploration L'idée, comme pour le programme
mis au point ci-dessus, consiste à ne balayer les nombres autour des multiples de 6. Pour cela, on traite d'abord le cas particulier
des nombres 2 et 3. On calcule la valeur de la super-primorielle (SP) pour
ces deux cas et on initialise une liste (L) de nombre premiers en y déposant
les nombres 2 et 3. La boucle d'exploration commence par 6 et
progresse par pas de 6. Cas ou i = – 1 (ce qui donne 5 pour le premier
passage avec i = 6). Si ce nombre ne divise pas SP alors il s'agit d'un
nouveau nombre premier. On calcule son exposant pour introduction dans la
super-primorielle. Et, bien sûr, ce nouveau premier est ajouté à la liste. Cas ou i =
+1 (ce qui donne 7 pour le premier passage avec i = 6). Même type de
traitement que ci-dessus. Fin de boucle (od). Édition de la liste et de la quantité d'éléments
qu'elle contient. En bleu, affichage des résultats de traitements.
On vérifie que le programme édite bien les 25 nombres premiers qui existent
jusqu'à 100. |
|
Voir Programmation – Index
Bilan sur la recherche
des nombres premiers
|
Un
premier programme exploite la primorielle
et détecte les nombres premiers au
moyen d'une instruction de calcul de PGCD. Intéressant, mais cette instruction "connait" les nombres premiers.
Intérêt comme exercice de programmation. Le
second programme exploite la super-primorielle
et ne fait aucune hypothèse sur la connaissance des facteurs premiers des
nombres. Elle calcule le PPCM
des nombres successifs. Procédé astucieux mais avec un inconvénient, la
super-primorielle devient vite un très grand nombre à manipuler. Néanmoins
Maple calcule les 9 592 premiers nombres premiers jusqu'à 100 000 en 12
secondes alors que Sp = 6,95… 1043 451. |
Grand Merci à Yves Roques pour une belle extension de cette page
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()