le petit théorème de Fermat et n puissance k moins n

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/09/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Théorie des Nombres
Débutants Général	Le petit théorème de Fermat			Glossaire Général
INDEX Théorie des nombres	Découverte	Exploration	Démonstration	Généralisation
	Perles et collier	Applications	Puissances	Avec Pascal
		Sommaire de cette page >>> n² – n >>> n³ – n >>> n⁵ – n >>> Analyse pour p suivants: de 7 à 17 >>> Bilan de divisibilité pour p de 2 à 53

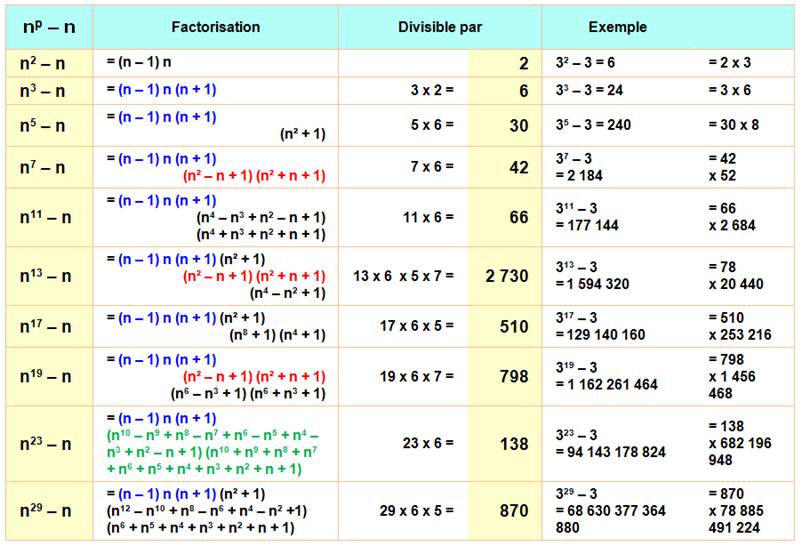
PETIT THÉORÈME DE FERMAT

Applications directes à n^p - n

Déductions immédiates du petit théorème de Fermat sur la forme cette forme polynomiale simple.

Exemple: n¹³ – n est divisible 2 730

n² – n divisible par 2
L'exposant 2 est un nombre premier. Application du PTF. Les trois formulations sont équivalentes.	n² – n = 2 k Ce qui veut dire que ce polynôme est divisible par 2; il est toujours pair. Ex: 3² - 3 = 9 – 3 = 6
Nous avons une confirmation directe sans le PTF. En effet, factorisons:	n² – n = (n – 1) n Succession de deux nombres, dont l'un est forcément pair et le produit est pair.

n³ – n divisible par 6

PTF direct avec 3

L'exposant 3 est un nombre premier.
Application du PTF:

Ce qui veut dire que ce polynôme est divisible par 3.

Ex: 3³ - 3 = 27 – 3 = 24

Factorisation

Elle nous montre que ce polynôme est divisible par 6.

n³ – n = (n – 1) n (n + 1)

Succession de trois nombres.

L'un d'eux au moins est pair, et

L'un d'eux au moins est divisible par 3.

n³ – n = 6 k

PTF supplémentaire avec 2

Cette indication nous incite à revoir le PTF sur ce polynôme de la manière suivant.

On montre que ce polynôme est aussi divisible par 2.

Divisible par 3 et par 2, il l'est par 6.

En mod 2:

Derrière le signe de congruence, n² est équivalant à n.

Récurrence

La divisibilité par 6 se démontre également facilement par récurrence.

Initialisation

n³ – n est divisible par 6 pour n = 0.

Calcul d'hérédité

Supposons la vraie pour k_n

n³ – n = 6k

Et calculons sont expression pour n +1

E_n+1 = (n + 1)³ – (n + 1) = n³ + 3n² + 3n + 1 – n – 1

= n³ – n + 3n(n + 1) = 6k + 3n(n + 1)

Or n et (n + 1) sont deux nombres consécutifs; l'un d'eux est pair est n (n + 1) est divisible par 2.

E_n+1 = 6k + 3 x 2h = 6 (k + h), divisible par 6.

Conclusion

Si la divisibilité par 6 est vraie pour n, alors elle est vraie pour n + 1, or elle est vraie pour 0; elle est toujours vraie.

Trois méthodes

Nous venons de voir trois méthodes pour démontre que n³ – n est divisible par 6:

par factorisation et constat de trois nombres consécutifs

par récurrence, et

par l'emploi du petit théorème de Fermat à répétition (pour p = 2 et pour p = 3).

n⁵ – n divisible par 30

Nous allons utiliser le PTF en cascade avec les nombres premiers successifs inférieurs à 5, soit ici: 2 et 3.

Les deux colonnes de gauche indiquent la propriété de base déduite du PTF.
La colonne centrale en blanc montre le calcul du modulo de la puissance concernée, ici 5.

Exemple de lecture: en modulo 3, le PTF nous dit que n³ – n est divisible par 3. En partant de n⁵ nous cherchons à sortir autant de cubes que possible, ici un seul. Chaque cube est remplacé par n en modulo 3 conformément à notre PTF. Au final n⁵est identique à n en modulo 3. Ils sont même reste lorsque divisés par 3. Leur différence n³ – n est divisible par 3.