NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/12/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Nombres PREMIERS
Débutants Nombres Premiers	Recherche de PRIMALITÉ				Glossaire Nombres Premiers
INDEX Nombres premiers Types de premiers	Crible d'Ératosthène	Presque-premiers	Pseudo-premiers	Carmichaël
	Divisibilité		Nombres de Poulet	Carmichaël - texte
	Primalité		Liste pseudo-P.
		Sommaire de cette page >>> Approche >>> Théorème chinois >>> Nombres pseudo-premiers >>> Propriétés >>> Pseudo-premiers d'Euler >>> Plus petit pseudo-premier >>> Pseudo-premiers forts

On dit primarité (français) ou primalité (avec teinture anglo-saxonne)

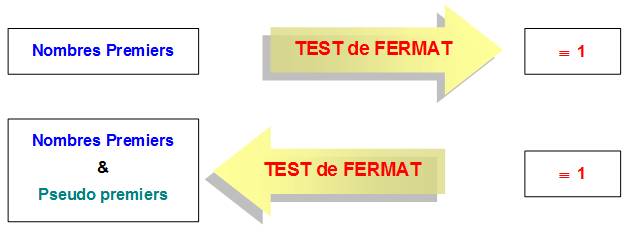
NOMBRES PSEUDO PREMIERS

S'ils n'existaient pas, il serait beaucoup plus facile de déterminer si un nombre est premier ou pas. Leur existence infirme la réciproque du Petit Théorème de Fermat.

Peu nombreux, mais bien embêtants …

Consultez la page Primalité pour une large introduction à ce sujet.

Anglais: Pseudo prime

APPROCHE

Approche

On s'intéresse à la puissance p de 2, à laquelle on retranche 2. Examinons la divisibilité ?

Cette valeur (2^p – 2) est souvent divisible par la puissance p elle-même.

Examinons les conditions pour que la divisibilité de 2^p – 2 par p soit assurée.

p premier, alors la divisibilité est assurée

p composé, alors pratiquement jamais divisible, mais il existe des cas de divisibilité

Exemples

p = 5	Premier	2^5 – 2	= 30 = 5 k	Bon
p = 4 = 2 x 2	Composé	2^4 – 2	= 14 4 k	Non
p = 341 = 11 x 31	Composé	2^341 – 2	= 341 k	Bon

Il semblerait donc que 2^p – 2

Est divisible par p si p est premier; et

On ne peut rien dire si p est composé.

Théorème chinois
Les Chinois formulent une hypothèse: Pour tout premier p, 2^p - 2 est divisible par p.
C'est vrai !	MAIS, la réciproque est fausse
C'est une conséquence du petit théorème de Fermat – Version faible. Si p est premier, les restes des divisions par p - d'un nombre quelconque et - de ce nombre à la puissance p sont égaux : (a^p – a) est divisible par p ou, plus mathématiquement: a^p – a 0 mod p Plus simplement: divisés par p, les nombres a et a la puissance p ont même reste. Autre formulation –Version forte En divisant les deux membres par p, à condition que a et p soient étrangers (premiers entre eux): a^p-1 – 1 est divisible par p	Effectivement, la réciproque est fausse, contrairement à la croyance chinoise et à ce que pensait également Leibniz. En 1819 Pierre Sarrus trouve une exception infirmant la réciproque. 2^341 – 2 est divisible par 341 et, pourtant 341 n'est pas premier: 341 = 11 x 31 341 est le plus petit entier composé ayant cette propriété. Ce contre-exemple montre que la réciproque du petit théorème est fausse. On ne peut pas compter sur ce théorème pour détecter les nombres premiers à coup sûr.

Nombres PSEUDO-PREMIERS ou Nombres CHINOIS

Nombres composés curieux qui se comportent comme des nombres premiers selon le test basé sur le petit théorème de Fermat – version forte: Le test de Fermat fonctionne comme un tamis qui laisse passer tous les nombres premiers. Mais hélas, qui en laisse passer quelques autres, les pseudo-premiers. Les nombres pseudo-premiers sont de la famille des presque premiers. En effet, avec le test de Fermat: Un nombre premier donne toujours le résultat attendu. Le résultat 1 est obtenu pour tous les nombres premiers et, aussi, quelques autres, les pseudo-premiers. Un nombre pseudo-premier en base a est appelé: nombre pseudo-premier de Fermat en base a ou a-PP.

Propriétés

341 est le plus petit pseudo-premier de base 2.

Ce qui signifie que 2³⁴⁰ – 1 est divisible par 341, bien que 341 soit composé et non pas premier.

Les pseudo-premiers sont relativement rares, pourtant en nombre infini

Jusqu'à	Pseudo-premiers	PP en base 2
20 000 000 000	882 206 716	19 865

Voici la liste de tels nombres jusqu'à 10 000 pour a = 2:

341, 561, 645, 1105, 1387, 1729, 1905, 2047, 2465, 2701, 2821, 3277, 4033, 4369, 4371, 4681, 5461, 6601, 7957, 8321, 8481, 8911.

Pour a = 3, on trouverait: 91 121 286 671 703

Pour a = 4, on trouverait: 15 85 91 341 435

Etc. Voir Liste de pseudo-premiers

Il y a en a une infinité pour chaque valeur de la base a.

Pseudo-premier d'Euler
Un pseudo-premier d'Euler n de base a est un nombre impair composé, n et a étant premiers entre eux, tel que: En effet: Tous les calculs qui suivent sont faits en mod p
Petit théorème de Fermat avec p premier et premier avec a.
Avec p premier autre que 2; p est alors impair.
En factorisant
En considérant chaque facteur
Or p = 2q + 1 et q = (p-1)/2

Plus petit pseudo-premiers
Le plus petit pseudo-premier dans sa catégorie:

Source Pomerance indiquée in fine

Pseudo-premiers forts
Nombre composé n = d 2^s + 1 Où d est impair tel que l'une des conditions suivantes soit satisfaite: Avec r compris entre 0 et s
Ils sont en quantité infinie pour chaque valeur de la base a
2-PPF	2047, 3277, 4033, 4681, 8321, 15841, 29341, 42799, 49141, 52633, 65281, 74665, 80581, 85489, 88357, 90751, …

Suite	Liste des pseudo-premiers Nombres de Poulet Nombres de Carmichaël Pseudo-premiers de Perrin Nombres premiers – Index
Voir	Décomposition Nombre en 161 038 Petit théorème de Fermat Théorie des nombres
DicoNombre	Nombre 341 Nombre 161 038
Sites	La page des nombres premiers de Chris Caldwell The Pseudoprimes to 25 10^9 by Carl Pomerance et al. Strong pseudoprime – Wikipedia OEIS A001567 – Fermat pseudoprimes to base 2, also called Sarrus numbers or Poulet numbers OEIS A005935 - Pseudoprimes to base 3 OEIS A020136 - Pseudoprimes to base 4 OEIS A005936 - Pseudoprimes to base 5 Autres références
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Premier/pseudo.htm