|
|||||||||||||||||||||||||||
![]()
|
Théorème
de Fermat-Wiles avec n = 3 Cas
de p² + 3q² = u3 Cette page contient une série de lemmes qui s'enchaînent pour trouver
les solutions de cette équation
diophantienne. Nous en sortirons avec une nouvelle expression des paramètres p et q
pour la démonstration de l'équation de Fermat avec les cubes. |
Cartographie de la démonstration
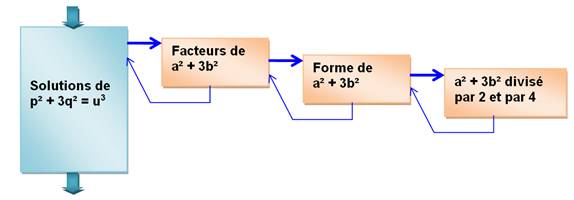
Suivre
les liens au fur et à mesure dans le texte
|
|
||
|
Ce que nous
avons
Ce qu'il faut
démontrer
Démonstration |
||
|
Que
dire du cube u3 = p² + 3q² ? Notations: P = un
nombre pair et I un nombre impair. |
p et q sont de parités opposées. Leur carré aussi. La somme est impaire, car: P²
+ 3I² I²
+ 3P² Donc:
u est impair. |
|
|
On
utilise ce nouveau lemme pour montrer que tous les
facteurs doivent être de la même forme. Attention:
ce lemme est un peu "costaud"! |
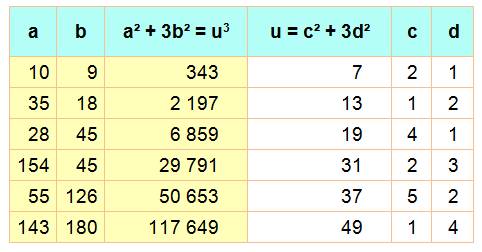
u3 = p² + 3q² alors u = a² +3b² |
|
|
Calcul |
Simple technique opératoire de l'algèbre |
|
Calcul
de u au cube avec a et b et mise
sous la forme recherchée. Première étape. |
u3 = p² + 3q² = (a² + 3b²)3 = (a² + 3b²) (a4 + 6a²b² + 9b4) = (a² + 3b²) (a4 + 12a²b² – 6a²b²+ 9b4) = (a² + 3b²) ( (a²
– 3b²)² + 3(2ab)² ) = (P²
+ 3Q²) ( R²
+ 3S²) |
|
Pour
simplifier le calcul, on pose momentanément: |
R = a² – 3b² S = 2ab |
|
Poursuivons
la mise en forme de cette expression. En effet, le produit de deux polynômes
en a² + 3b² est aussi un polynôme de cette forme. |
(a² + 3b²) (R² + 3S²) = a² (R² + 3S²) + 3b² (R² + 3S²) = a²R² + 3a²S² + 3b²R² + 9b²S² = a²R² – 6abRS + 3a²S² +
3b²R² + 6abRS + 9b²S² = (aR – 3bS)² + 3(aS
+ bR)² |
|
Soit
en remplaçant dans u au cube. |
u3 = (a
(a² – 3b²) – 3 (b . 2ab))²
+ 3 (a
. 2ab + b (a² – 3b²))²
=
(a3 – 3ab² – 6ab²)² +
3 (
2a²b + a²b – 3b3 )² = (a3 – 9ab²)²
+ 3(3a²b – 3b3)² |
|
Et
en reprenant la forme en p et q. |
u3 = (a3 – 9ab²)²
+ 3(3a²b – 3b3)² = p² + 3q² |
|
En
égalant terme à terme nous obtenons une solution de l'équation baptisée:
E223. |
p =
a3 – 9ab² q =
3a²b – 3b3 Solution de p² + 3q² = u3 |
|
p et q sont premiers entre
eux. |
aussi le sont a et b sinon leur facteur commun diviserait p et
q. |
|
p et q sont de parités
opposées. |
aussi le sont a et b car: a et b impairs, alors q = impair – impair = pair p = impair – impair = pair Impossible, p et q sont de parités
opposées. a et b pairs, alors q = pair – pair = pair p = pair – pair = pair Impossible, p et q sont de parités
opposées. |
Retour
vers la page PGCD faisant appel à ce lemme
|
|
||
|
Ce que nous
avons
Ce qu'il faut
démontrer
a² + 3b² = k (c² + 3d²) Observation
Démonstration |
||
|
On
va démontrer que si Alors |
a²
+ 3b² = k (c² + 3d²) k peut être aussi
petit que l'on veut, ce qui est impossible. |
|
|
Soit
k un facteur impair positif |
a² + 3b² = k f k > 1 pour que la
factorisation existe. |
|
|
Prenons
l'expression classique de la division par k
avec c et d les restes; ceux-ci sont inférieurs au diviseur k. Si
nous prenons c et d en relatif (positif ou négatif), nous pouvons même dire
que leur valeur absolue est inférieure à ½. |
a = mk + c avec c <
k b = nk + d avec d <
k Nouvelles valeurs de c et d a = mk b = nk |
|
|
Reprenons
l'expression: |
a² + 3b² = (mk = m²k² 3n²k² = k (m²k + c² + 3d² |
|
|
Or
cette expression est divisible par k. Le
premier terme de notre expression est divisible pas x, et le reste doit
l'être aussi. |
a² + 3b² = k f (notre hypothèse de
départ) c² + 3d² = k h (h un nouveau facteur) |
|
|
Nous
aurons besoin de cette relation plus loin. |
k est inférieur à h |
|
Que
vaut le produit en reprenant nos inégalités? |
kh = c²
+ 3d² < (k/2)² + 3(k/2)² = k²/4 + 3k²/4 = k² |
|
Somme
de deux carrés (a² + 3b²), kf est positif; k et f
aussi. Somme
de deux carrés (c² + 3d²), kh est positif; k et h
aussi. Nous
pouvons diviser par k sans changer l'inégalité. |
kh < k² h < k |
|
L'expression
c² + 3d² est bien positive. On
sait que c et d ont été choisis positifs. |
Imaginons le cas où: c² + 3d² = 0 c
= d = 0 |
|
Reprenons
les divisions. Les
nombres a et b seraient divisibles par k. Ce qui contredit le fait qu'ils
sont premiers entre eux. |
a = mk b = nk Or PGCD(a, b) = 1
|
|
Bilan
à ce point |
a² + 3b² = kf = kK + c² + 3d² Avec c² + 3 d² non nul
et c² + 3 d² = kh avec h <
k |
|
Cherchons
à rendre c² + 3d² primitif |
c²
+ 3d² = g² (C² + 3D²) |
|
Si
g est le PGCD de c et d. Le
PGCD des facteurs non communs (C et D) est égal à 1. C et D sont premiers
entre eux. |
g = PGCD (c, d) c = gC d = gD avec PGCD (C, D) = 1 |
|
Est-ce
que g² divise h?
|
kh = c² + 3d² = (gC)² +3(gD)² = g²(C² + 3D²) |
|
Alors
g² divise |
k et ou h |
|
Hypothèse:
soit p un diviseur premier de g mais pas de h |
kh = g² (C² + 3D²) |
|
Donc
p divise à la fois g et k (pas h). |
k = Kp g = Gp |
|
Pour
a et b, nous montrons qu'ils sont divisibles par p. Or,
ce n'est pas possible. Car a et b sont premiers entre eux. |
a = mk = mKp b = nk |
|
Contradiction!
Il n'existe pas de premier p divisant g sans diviser h. C'est l'inverse: |
g divise h et même: g² divise h h =
g² z |
|
En
divisant kh par g² Expression
désormais réduites à des nombres
premiers entre eux. |
kh = g² (C² + 3D²) kg²z = g² (C² + 3D²) kz =
C² + 3D² avec PGCD (C, D) = 1 |
|
Alors, avons-nous atteint notre but: |
k est-il de la forme
p² + 3q² ? |
|
Si
k n'est pas de cette forme, il existe un w tel que: |
w divise z sans
être de la forme: p² + 3q² |
|
w
n'est pas nul. |
Il serait de cette forme non autorisée: w = 0² + 3 x 0² |
|
w
est donc plus grand que 1 tout en étant plus petit que z puisqu'il le divise.
|
1 < w < z |
|
En
cascade, w est inférieur à k |
h = g²z
h < k (voir zone jaune
ci-dessus) z < k w < z < k |
|
Nous
venons de prouver que l'existence de k entraîne celle de w, plus petit et de
même forme. Le raisonnement se tiendrait de la même manière pour trouver un
facteur w' encore plus petit. Nous entamons une descente infinie. Hypothèse fausse. Les facteurs sont bien de la forme p² + 3q². |
|
|
|
||
|
Si
a² + 3b² possède un facteur impair qui
n'est pas de cette forme, alors le quotient
lui aussi à un facteur impair qui n'est
pas de cette forme. Ce que nous
avons
Ce qu'il faut
démontrer
Démonstration |
||
|
Le
nombre f étant un facteur, il existe g
tel que: |
f.g = a² + 3b² avec
f impair et non de cette forme. |
|
|
Les
facteurs premiers de g sont: |
g = p1
. p2 . … . pn |
|
|
Supposons
que tous les facteurs impairs de g: |
sont de cette forme: p² + 3q² |
|
Nous allons nous occuper des facteurs pairs qui vont
laisser leur trace par une forme en p² + 3q² alors que les facteurs impairs,
par hypothèse en p²+ 3q², vont se simplifier. |
|
|
Toute
apparition du facteur 2 peut être remplacée par 4. |
Si 2 divise a² + 3b², alors
4 aussi. Si f est impair (non divisible par 4),
alors toute apparition de 4 divise g de manière à diviser f.g. |
|
Nous
pouvons diviser toutes les apparitions de 4. |
f.g = a² + 3b² Ces deux membres sont simplifiés de tous les
4 qui y apparaissent tout en conservant la même forme en p² + 3q². |
|
Tous
les facteurs impairs de g sont en p² + 3q² |
On peut diviser a² + 3b² par ces facteurs. |
|
Après
les facteurs pairs (en 2) puis les facteurs impairs de g, il nous reste: |
f = p² + 3q² Ce qui est contraire à notre hypothèse. Notre supposition est fausse. Les facteurs de g ne sont pas en p² + 3q². |
|
|
||
|
Ce qu'il faut
démontrer
Démonstration |
||
|
Divisible
par 2, donc: Car, Avec
deux pairs, les carrés sont pairs. Avec
deux impairs, les carrés sont impairs et la somme paire. |
a et b sont de même parité. |
|
|
Si
a et b sont pairs, notre expression est
divisible par 4. |
a = 2c et b = 2d a² + 3b² = 4c²+ 12 d² divisible par 4 |
|
|
Si
a et b sont impairs, alors : Ex: 7 = 2x 4 – 1; 9 = 2x 4 + 1 Les nombres impairs sont
tous de part et d'autre des multiples de 4. |
a = 4m b = 4n |
|
|
Addition
et soustraction |
|
|
|
Si 4 divise a + b, prenons quatre fois notre expression et
"éclatons" le 4 selon notre forme. En
arrangeant le calcul de façon adéquate, nous retrouvons notre forme de départ |
4(a² + 3b²) = (1² + 3 x 1²) (a² +
3b²) = a² + 3b² + 3a² + 9b² = a² – 6ab + 9b²+ 3a² +
6ab +3b² = (a – 3b)² + 3(a + b)² |
|
Ce
qui implique les divisibilités suivantes: |
4 divise (a – 3b)² +
3(a + b)² 4 divise (a – 3b)² 4 divise 3(a + b)² |
|
Selon
notre hypothèse: On
déduit: |
4 divise a + b 4 divise a + b – 4b = a – 3b |
|
En
reprenant notre expression: Au
premier membre, chaque terme est divisible par 4 et leur carré par 4². |
(a – 3b)² + 3(a + b)² = 4(a² + 3b²) Chacun des membres de l'égalité est
divisible par 4² |
|
Au
second membre, outre le facteur 4, c'est l'autre facteur qui est divisible
par 4. |
4(a² + 3b²) divisible
par 4² (a² + 3b²) divisible par 4 |
|
Si 4 divise a – b, même raisonnement avec ici: 4
divise a + 3b (au lieu de a – 3b) |
4(a² + 3b²) = (1² + 3 x (-1)²) (a²
+ 3b²) = a² + 3b² + 3a² + 9b² = a² + 6ab + 9b²+ 3a² –
6ab +3b² = (a + 3b)² + 3(a – b)² Etc. |
|
Dans
tous les cas: |
(a² + 3b²) est
divisible par 4 |
![]()
|
Retour |
|
|
Suite |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/FERMAT/Fer3PGCD.htm |
![]()