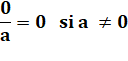|
|||||||||||||||||||||||||||
![]()
|
La France
est le seul pays du monde où, si vous ajoutez dix citoyens à dix autres, vous
ne faites pas une addition,
mais vingt divisions. Pierre Daninos |
Voir Pensées & humour
|
DIVISION
|
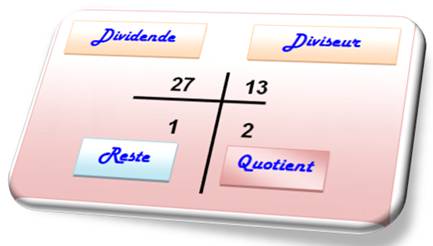
27 / 13 =
2 reste 1. ou 27 = 13 x
2 + 1 |
|
Notations: on ne sait jamais où les chercher !
|
|
|
|
|
Définition
La dernière ligne indique que le reste doit
être inférieur au diviseur, sinon, comme on disait à l'école, il y va une
fois de plus.
De
plus, si a n'est pas divisible par b, alors Anglais Given any integer a and b, with a > 0, there
exist unique integers q and r such that
If a is not divisible by b, then r satisfies the
stronger inequality |
|
Voir Jeux du 100 en 6 chiffres
(Hectoc)
|
|
||
|
|
||
|
On forme une progression arithmétique, de raison
a: Exemple avec a = 13 et b = 27: |
… , b – 3a , b – 3a , b – a , b + a , b + 2a , b + 3a , … –25, –12, 1, 14, 27, 30 |
|
|
Choix de cette progression: Du fait de la définition de la
division: Notez l'air de famille avec le
reste. |
b – k.a b = a.q + r ou r = b – a.q |
|
|
Dans cette suite, il existe un plus petit nombre positif. |
Ici, c'est 1
que l'on baptise qui n'est autre que r. Et r est plus petit que a.
|
|
|
Avec cette valeur de r, on calcule q |
b = a . q + r |
|
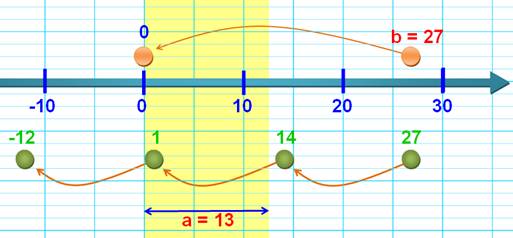
Illustration du fait que r est bien inférieur à a
|
En partant de b = 27, je retire autant de
fois a = 13 que je le peux, sans passer en négatif. Ce point est obtenu pour r = 1 et, il est
bien situé dans la zone de 0 à a = 13 (jaune). |
|
|
|
|||
|
Nous connaissons déjà. Supposons l'existence d'un autre
couple qui satisfasse les mêmes conditions. |
q et r d |
q' et r' = r – r' |
|
|
Selon la définition de la division
les conditions sont les suivantes: |
b = a . q + r
|
b = a . q' + r'
|
|
|
Différence des restes: première évaluation. Avec les égalités de la division. |
r = r' = r – r' = d = |
b – a.q b – a.q' a (q – q') a.Q |
|
|
Le quotient a est diviseur de la
différence. Or, un
diviseur est plus petit que le nombre qu'il divise. |
a a < |
d |
|
|
Différence des restes: seconde évaluation. Avec les inégalités de la division. Le nombre a est plus grand que
r et que r'; il est a fortiori plus
grand que leur différence. |
a > |
d |
|
|
Ce raisonnement par
l'absurde (faire une hypothèse contraire à ce qui doit être démontré)
aboutit à une contradiction. l'hypothèse est fausse et l'affirmation que q et
r sont uniques est vraie. |
|||
|
impliquant parties entières et
décimales |
|
||
|
Unicité |
|
|
|
|
Si les
conditions suivantes sont
vérifiées pour q et r |
b = a . q + r |
|
|
|
On peut
aussi les écrire de la façon suivante |
b/a = q + r/a |
|
|
|
Avec r/a
plus petit que 1 |
q est la partie entière de b/a |
r/a en est la partie décimale |
|
|
Or la
partie entière d'un quotient est unique Même chose
pour r qui est égal à b – a.q |
q est unique |
r aussi |
|
|
Existence |
|
|
|
|
Supposons
les deux entiers définis par |
q = partie entière de b/a |
r = b - a. q |
|
|
La
première partie de la définition de la
division est vérifiée |
b = |
a. q + r |
|
|
Le
quotient b/a diminué de sa partie entière q donne sa
partie décimale |
partie
décimale = b/a – q |
||
|
Elle est
comprise entre 0 et 1 |
|
||
|
Or cette
expression peut être évaluée à partir
de l'expression de b |
b = b/a = b/a - q = |
a. q + r q + r/a r/a |
|
|
Remplaçons
dans l'inégalité |
|
||
|
En multipliant
par a* |
|
||
|
*Nous
sommes toujours dans le monde des entiers positifs On
pourrait reprendre toutes ces démonstrations pour tenir compte de tous les
cas de figures Ce n'est
pas l'objet de ce site à vocation d'initiation seulement. |
|||
Bilan
|
La division est parfaitement définie, et
nous savons qu'elle est unique. Elle n'admet qu'un seul quotient et qu'un
seul reste. Nous allons utiliser ces résultats pour trouver le plus grand
commun dénominateur (PGCD) de deux nombres et découvrir l'algorithme
d'Euclide. |
|
|
|||
|
|
Impossible |
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
On écrit en abrégé |
|
||
|
|
Si un nombre premier p
divise le produit de deux nombres entiers b.c, alors p divise b ou c. |
||
|
|
Si a et b sont premiers entre eux et si a divise
le produit bc, alors a divise c. |
||
Anglais
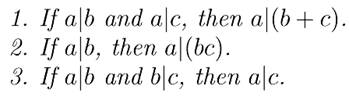
Divisibilité – Démonstration
|
Si ac Le nombre c étant non nul, c'est le deuxième facteur qui l'est: ak – b
= 0. C'est la définition de la divisibilité de a par b. |
![]()
|
Suite |
|
|
Autour |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/Division.htm
|
![]()