NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 17/05/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Théorème de Fermat-Wiles
Débutants Triplets de Pythagore	Cas n = 4			Glossaire Puissances
INDEX Puissance Décomposition	Théorème général	Triplets 422 à 444	Équation 442 (démo)
		Sommaire de cette page >>> Un carré dans le triplet >>> Deux carrés >>> Bilan E2 et E4 >>> Avec des cubes >>> Bilan E3 et E6

Équations diophantiennes

entre Pythagore et Fermat

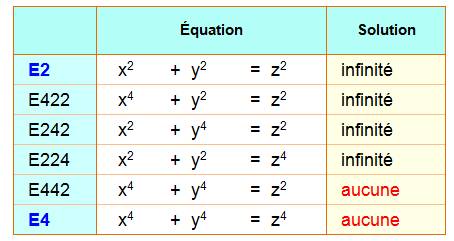
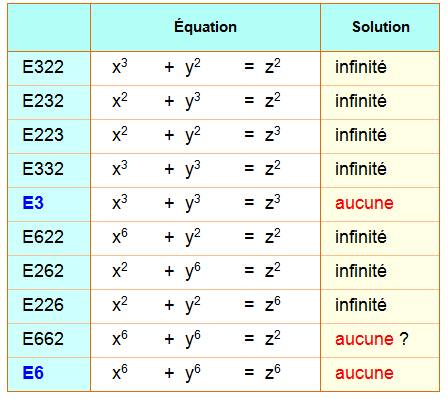
du type: x⁴ + y² = z² (E422)

Équation à mi-chemin entre un triplet de Pythagore: x² + y² = z² (E2)

et l'équation de Fermat pour n = 4: x⁴ + y⁴ = z⁴ (E4).

Nous envisageons les triplets de Pythagore tout en examinant les cas où x ou y ou z seraient eux-mêmes des carrés voire des cubes.

x⁴ + y² = (x²)² + y² = z²

Un carré dans le triplet de Pythagore
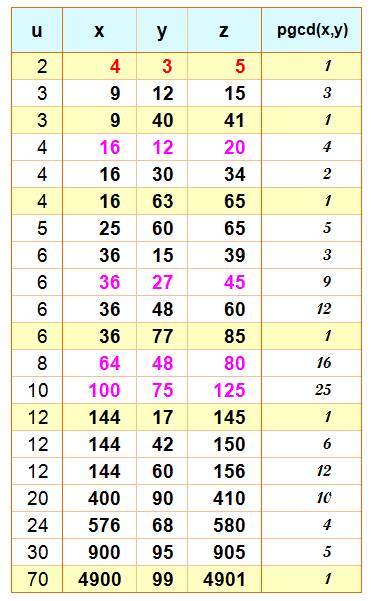
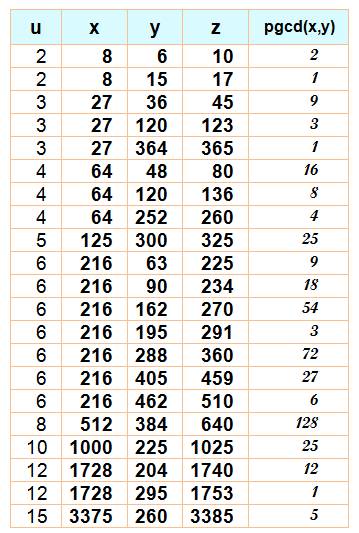
Nous sommes familiers avec les triplets de Pythagore. Se peut-il que l'un ou plusieurs de ses termes soient lui-même un carré. Le cas d'un seul carré est vite vu! Le plus connu des triplets donne un exemple.	avec x = u²
Tableau des triplets dont un des termes est un carré pour u et y de 2 à 100. Exemple de lecture: u = 3 x = 3² = 9; ce qui donne: (3²)² + 12² = 81 + 144 = 225 = 15² Les triplets en jaune sont primitifs (le plus grand commun diviseur de x et y est 1; ces deux nombres sont étrangers). Les triplets en mauve sont les triplets filles du triplet primitif en rouge (4² + 3² = 5²). Il existe une infinité de triplets de Pythagore dont l'un des termes est un carré. Soit une infinité de solutions à u^4 + y^2 = z^2
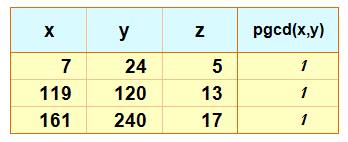
La puissance quatrième peut porter sur le z. Exemple: 7² + 24² = 625 = 5^4

Deux carrés
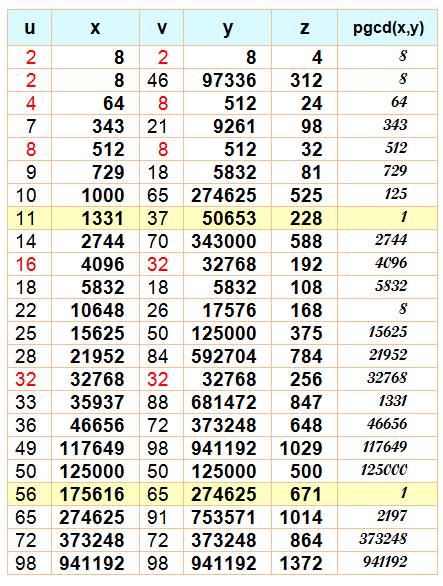
Le cas de deux carrés nous met sur les pas de Fermat. En effet, il n'y a aucune solution à cette équation. Cette équation (notée E442 ou E42) sans solution indique que: La somme de deux puissances quatrièmes n'est jamais un carré: u^4 + v^4 = z^2 n'a pas de solution. Voir Démonstration	avec x = u² et y = v² Évidemment si cette somme n'est jamais un carré, a fortiori, elle n'est jamais une puissance quatre (qui n'est autre qu'un carré au carré). E4 n'a pas de solution. La somme de deux puissances quatrièmes n'est jamais une puissance quatrième: u^4 + v^4 = z^4 n'a pas de solution.

Bilan E2 et E4
Avec l'un des trois termes au carré (qui devient une puissance quatrième), le triplet de Pythagore possède toujours une infinité de solutions. Dés la présence de deux carrés (qui deviennent des puissances quatrièmes), le triplet n'a plus aucune solution.

Avec un cube
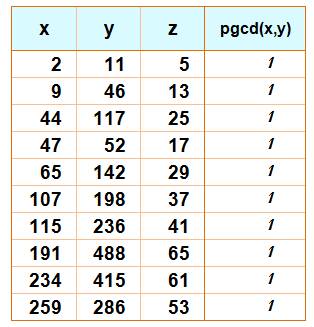
Pour prolonger notre exploration, voyons le triplet avec un cube en z. E223: x² + y² = z^3 Exemple: 2² + 11² = 125 = 5^3	Voir Suite
L'un des termes x ou y peut être aussi un cube. x^2 + y^2 = z^2 avec x = u^3 E622: u^6 + y^2 = z^2 Exemple: 2^6 + 6^2 = 100 = 10^2
Les deux termes x et y sont des cubes. En rouge, les puissances de 2. E332: x^3 + y^3 = z^2 Exemples: 2^3 + 2^3 = 16 = 4^2 2^3 + 46^3 = 97 344 = 312^2 Si E332 a des solutions c'est le cas aussi pour E322 et 232.

Bilan E3 et E6
Un triplet de Pythagore avec un terme ou deux au cube et non au carré: il y a une infinité de solutions. Avec les trois au cube (E333 ou E3, aucune solution (théorème de Fermat-Wiles). Un triplet de Pythagore dont un terme est un cube (qui devient une puissance sixième): infinité de solutions. Avec deux puissances sixièmes, je ne dispose pas de la réponse. Il me semble qu'il n'y a pas de solution. Avec les trois puissances sixièmes, le carré des puissances troisièmes, il n'y pas de solution.

Suite	Équation E442 x^4 + y^4 = z^2 – Démonstration
Voir	Théorème de Fermat-Wiles Nombres de Leyland Puissance 4
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/FERMAT/Fe422.htm