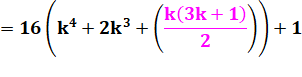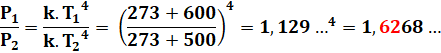|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Caractérisation des NOMBRES BICARRÉS Propriétés des nombres en
puissance de 4. |
Anglais: Biquadratic
numbers or tesseractic numbers
|
|
|
|
Notez la particularité du 2 (en bleu), avec
3 et plus ça ne marche pas! Voir Puissances à étages
Voir Derniers chiffres des bicarrés
|
|
|
|
|||
|
La puissance quatrième
d'un nombre N - pair est de la forme 16n - impair est de la forme 16n +
1 avec n
|
|||
|
N est pair |
N |
= 2k |
|
|
Sa puissance quatrième |
N4 |
= 16k4 = 16n |
|
|
N est impair |
N |
= 2k + 1 avec k |
|
|
Sa puissance quatrième |
N4 |
= (2k + 1)4 |
|
|
|
= 16k4 + 32k3 + 24k2
+8k + 1 |
||
|
Mise en facteur partielle |
|
|
|
|
Est-ce que la fraction est entière ? |
Si k = 2h Si k = 2h + 1
|
alors k est divisible par 2. alors 3k + 1
est pair et divisible par 2. Dans les deux cas, le numérateur est divisible
par 2 et la fraction est entière. |
|
|
Bilan |
N4 |
= 16n + 1
|
|
|
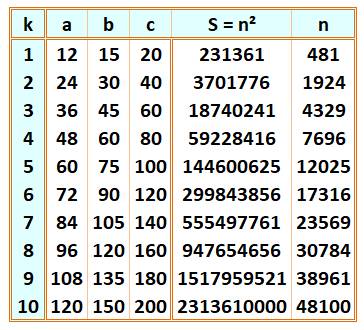
481² = 124 + 154 + 204 1924² = 244 + 304
+ 404 Tous les multiples de la première configuration produisent le même
motif en somme de trois cubes égalant un carré. Ce sont les seuls cas. Exemple jusqu'à k = 10
|
|
|
|
|
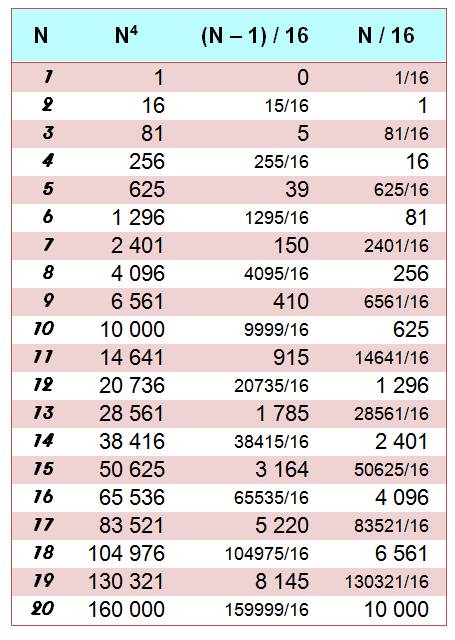
Table des puissances quatrième des nombres de 1 à 20. La troisième colonne montre la forme en 16n + 1 pour les nombres impairs et la quatrième
colonne montre la forme en 16 n pour les nombres pairs.
|
|
Voir Tables
– Index
|
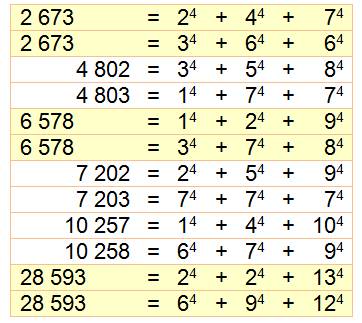
Propriété et méthode Chaque puissance 4 des nombres est la somme de "paquets" de
nombres consécutifs de taille de plus en plus grande. Sélectionner k nombres successifs une fois sur deux, avec k + 1 à
chaque itération. Avec n paquets retenus, la somme de ces n paquets vaut n4. Exemple: k = 1 => 1 OK; k = 2 => 2 et 3 ignorés; k
= 3 => 4, 5, 6 OK.
|
Voir Brève
47-933
|
|
|
|
Impossibles Les équations diophantiennes
suivantes n'ont pas de solutions: x4 + y4 = z4 x4 + y4 = z2 et x4 – y4 = z2 >>> x4
– y4 = 2z2 Possibles Euler pensait que l'équation: x4
+ y4 + z4 = t4 n'avait pas de
solution. Or depuis, des contre-exemples ont été trouvés. Les équations suivantes
possèdent également de multiples solutions: x4 + y4 + z4
= 2t4 x4 + y4 + z4
+ t4 = u4 x4 + y4 + z4
+ t4 + u4 = v4 Ex: 24 + 24 + 34
+ 44 + 44 = 54 = 16 + 16 + 81 + 256 + 256 =
625 x4 + y4 + z4
+ t4 + u4 + v4 = w4 Ex: 24 + 44 + 64
+ 64 + 64 + 74 = 94 = 16 + 256 +
3x1296 + 2401 = 6 561 x4
+ y4 = z4 + t4 x4
+ y4 + z4 = t4 + u4 Ex: 54 + 54 + 64 + 84 = 34
+ 94 = 625 + 625 + 1296 + 4096 = 81 + 6561 = 6642 Exemples de nombres
Il existe une infinité de
solutions à: x4 + y4 + z4 + t4
= (x + y + z + t)4 |
|
Voir Suite et autres exemples / Notations de ce genre d'identités
|
La
puissance rayonnée par un corps chauffé
croît comme la puissance quatrième de sa température
absolue. La
puissance rayonnée d'une étoile est proportionnelle au carré du rayon de
l'étoile et à la puissance quatrième de sa température de surface. La
luminosité d'une étoile s'exprime par L = 4 Découverte en 1879 par Joseph Stefan
(1835-1897) et démontrée en 1884 par Ludwig Boltzmann (1844-1906). Exemple Une
surface porte à 600°C rayonne 62% d'énergie de
plus que celle portée à 500°C Calcul
|
Formule de l'aérodynamisme
|
Cette loi de la physique stipule essentiellement que lorsque
vous doublez la surface à l’avant d’un objet, vous doublez
aussi la résistance que l’air exerce sur lui. Mais si vous doublez la
vitesse, la résistance quadruple alors. C’est un phénomène qui se produit parce que la surface et la
résistance ont une relation linéaire, alors qu’avec la vitesse, la résistance
est liée de manière exponentielle. Par conséquent, plus vous allez vite, plus il est difficile
de lutter contre la force de l’air, de sorte que la surface et ses formes
doivent jouer en votre faveur. Il était prévisible que l’aérodynamique deviendrait une obsession
pour les constructeurs automobiles. L’inventeur autrichien Edmund Rumpler a
conçu une voiture en forme de goutte d’eau en 1921, |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()