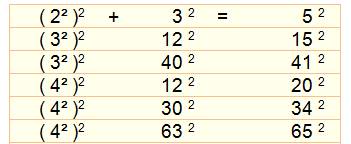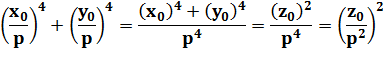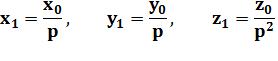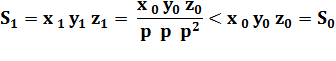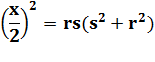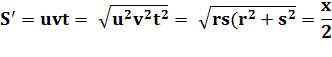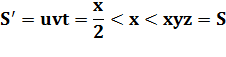|
|||||||||||||||||||||||||||||
![]()
|
Équation
diophantienne E422 x4
+ y4 = z2 Équation à mi-chemin entre un triplet de
Pythagore: x² + y² = z² (E2) et l'équation de Fermat pour n = 4: x4
+ y4 = z4 (E4). Comme pour E4, cette équation diophantienne n'a
pas de solution, autre que triviale (telle que xyz Vous savez que la démonstration existe et qu'elle a été conduite
rigoureusement. Vous savez aussi que les mathématiciens peuvent la présenter
en termes très concis car ils supposent un certain bagage acquis. Ici, je
vais la présenter dans son principe général. Mon but: développer cette
démonstration dans ses grandes lignes pour la rendre abordable au plus grand
nombre. J'ai pu voir au moins trois façons de résoudre ce problème. J'en
aborde deux: une conclusion par contradiction
et une autre via la descente infinie de
Fermat. La troisième solution fait appel à la théorie des anneaux. |
|
|
||
|
|
|
|
|
|
Aucun triplet de
Pythagore ne comporte deux termes carrés.
|
|
|
il y a une infinité de tels triplets,
à commencer par le plus célèbre d'entre tous: 3² + 4² = 5², avec le 4 qui est
bien un carré. |
|
|
|
|
||
|
|
|
|
|
|
Il existe une solution x, y, z en entiers
positifs telle qu'aucune autre solution n'a une valeur plus petite pour z. |
|
|
|
Notre choix conduirait à une autre solution x1,
y1, z1 avec z1 < z. Ce qui va contredire notre hypothèse disant que z
est le plus petit. |
|
|
|
Triplets de Pythagore: |
|
In fine vous trouverez la solution en raccourci.
En voici le détail:
|
|
||
|
|
S = xyz S0 = x0 y0 z0
Le plus petit produit avec les nombres x, y et z. |
|
|
La notation (x, y, z)
est une abréviation de PGCD (x, y,
z). Si le PGCD est égal à 1, les nombres sont premiers entre eux (on dit
aussi: étrangers). |
Alors, il existe un nombre p divisant x0
et y0 En utilisant notre équation, on peut écrire:
Donc p² divise z0. |
|
|
|
|
|
|
|
|
|
|
|
Cette inégalité (S1 < S0)
est impossible. Et le facteur p est égal à 1. Ce qui veut dire que ces
nombres étaient déjà premiers entre eux:
|
|
|
|
Cette nouvelle équation est un triplet de Pythagore primitif,
solution de (X)² + (Y)² = z². Avec X et Y les carrés de x et y. |
|
|
|
||
|
|
|
|
|
|
x² = 2ab y² = a² – b² z =
a² + b² avec: 0 < b < a (a, b) = 1 a ou
b pair |
|
|
Un carré est toujours divisible par 4 ou alors
il donne un reste de 1. On dit qu'il est congru à 0 ou 1 mod 4. |
Si a est pair et b impair: Le carré de a est divisible par 4 et:
Or un carré est congru à 0 ou 1 mod 4. Donc cette relation est impossible et b est pair. |
|
|
|
||
|
|
Le nombre b est pair. Le nombre a est impair Et le nombre y sera impair pour que l'égalité soit
satisfaite: b² + y² = a² |
|
|
|
Les trois termes sont premiers entre eux. Alors: (b, y, a) = 1 |
|
|
|
Le triplet (b, y, a) forme une autre solution
primitive de X² + Y² = z². |
|
|
|
b
= 2rs y
= s² – r² a
= s² + r² avec: 0
< r < s (r,
s) = 1 r ou s pair |
|
|
Si (a, b) = 1,
alors (a, b, a² + b² ) = 1. En effet: si p est facteur
commun de a et (a² + b²), c'est-à-dire, si p divise a² + b², et que p divise a, alors il divise b; p
divise à la fois a et b ce qui est impossible car (a, b) = 1. Donc p = 1 et
(a, a² + b² ) = 1. Même chose pour
(b, a² + b²) = 1. |
|
|
||
|
|
|
|
|
|
x est le (seul) nombre pair du triplet. |
|
|
|
(r, s²+r²) = (s, s² + r²) = 1 |
|
|
|
r, s et s² + r² sont des carrés parfaits. r = u² s = v² s² + r² = t²
|
|
|
|
(r, s, s² + r² ) = 1 |
|
|
|
s² + r² = t² qui donne u4 + v4 = t2 |
|
|
|
|
|
|
|
|
|
|
|
Impossible! L'hypothèse que l'équation
|
|
|
|
|
|
|
|
![]()
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/FERMAT/Fe42Dem.htm |
![]()