|
|||||||||||||||||||||||||||||||||||||
![]()
|
Divisibilité d'une somme de puissance (1/2) Surprenant! La somme des puissances des nombres
consécutifs est presque toujours divisible par le nombre qui suit. |
|
|
||
|
Sur la page précédente nous avons montré que N = 7 divise la somme
des puissances impaires (n
= 2k + 1) de cette somme jusqu'à 6 (= 7 - 1) Voici quelques Qu'en
est-il d'une m |
7 | 1n +
2n + 3n + 4n + 5n + 6n pour n = 2k+ 1 n = 1,
S = 21 = 7 x 3 n = 3,
S = 441 = 7 x 63 n = 5,
S = 12201 = 7 x 1743 n
= 7, S = 376761 = 7
x 53823 |
|
Voir Somme des
carrés de 1 à n
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
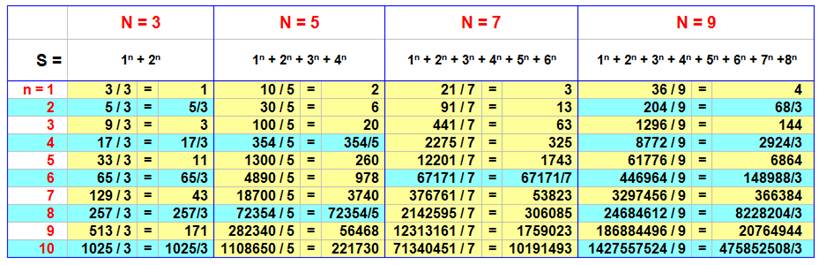
Pour différentes valeurs de N
impaires, nous allons constituer le tableau montrant la divisibilité de la
somme S. S est la somme des puissances n des
nombres entiers consécutifs jusqu'à N non compris. Les cases jaunes indiquent la
divisibilité par N (résultats entiers); les cases bleues montrent la
non-divisibilité (résultats fractionnaires). Exemple: 13 + 23 + 33
+ 43 = 100; le nombre suivant est 5; il est impair et la somme est
bien divisible par 5.
Une observation de ce tableau (et,
c'est valable pour sa suite) montre que la divisibilité est vraie pour tous
les n impairs. Normal, c'est la démonstration
vue en page précédente. En outre, certaines valeurs paires
de n dont également divisibles:
Voici le tableau récapitulatif pour
N impair:
Conclusion Pour la somme de N – 1 puissances, N
étant impair: N | 1n + 2n
+ 3n + ... + (N – 1)n
N divise cette somme sauf si N = 3 + 6k et n est p ou N |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
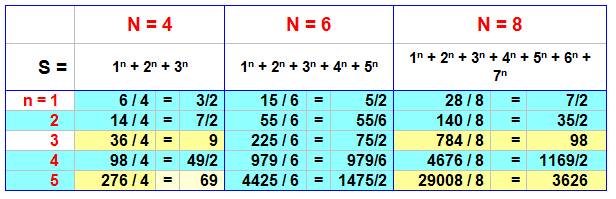
Même démarche que pour les valeurs
de N impaires.
Les fractions témoignent de la non-divisibilité. Une observation de ce tableau (et,
c'est valable pour sa suite) montre que la divisibilité est vraie
Voici le t
Conclusion Pour la somme de N – 1 puissances, N
étant pair: N | 1n + 2n
+ 3n + ... + (N-1)n N divise cette somme si N = 4 k et n est impair. |
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette
page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/SomPuiss.htm
|
![]()