collection de nombres, divisibilité par 7

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/01/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DIVISION
Débutants Division	Divisibilité				Glossaire Division
INDEX Divisibilité	Introduction		Divisibilité par 7, 11 et 13	Par 7
	Critères généraux		Divisibilité par 73, 137 …	Par 11, 101, 99, 999
		Sommaire de cette page >>> Propriété des multiples de 7 >>> Petits nombres >>> Nombres de taille moyenne >>> Grands nombres – Paquets de 3 >>> Exemples de calcul de divisibilité par 7 >>> Grands nombres – Paquets de 2 >>> Méthode générale avec clé de divisibilité >>> Puissances 7 et divisibilité par 7 >>> Forme divisible par 7

DIVISIBILITÉ par 7

Critères de divisibilité par 7. Comment s'y prendre? Plusieurs méthodes.

Devinette

Est-ce que 421 435 est divisible par 7 ?

Solution

Repdigit

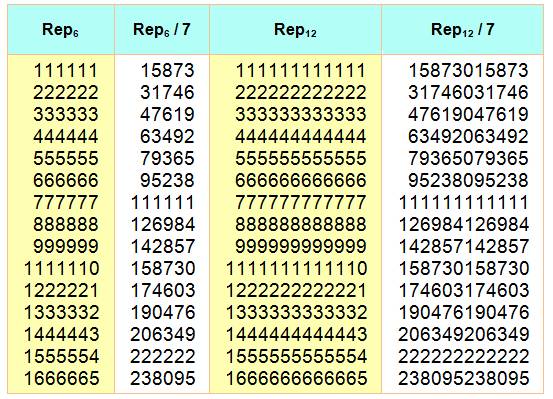
Les repdigits de k fois six chiffres sont divisibles par 7

Au-delà des repdigits, les nombres incrémentes du repunit de k fois six chiffres sont également divisibles par 7.

Rien de magique, une fois que l'on sait que 111 111 est divisible par 7. Tous ses multiples le sont également.

Voir Nombre 111 111

Plusieurs méthodes pour tester la divisibilité par 7

Tout nombre	Les deux méthodes les plus pratiques.	>>>
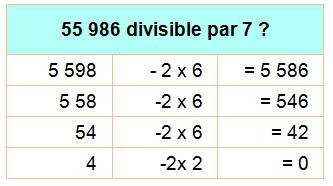
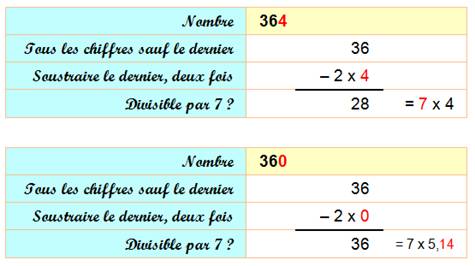
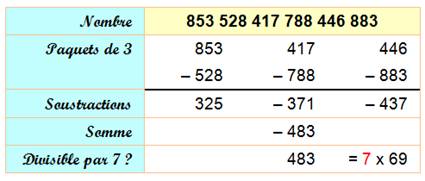
< 4 chiffres	Soustraction de 2 fois les unités. Efficace aussi pour grands nombres.	>>>
de 3 à 6 chiffres	Additionner 3 fois le chiffre de poids fort.	>>>
> 5 chiffres	Addition-soustraction par tranches de 3 chiffres.	>>>
"	Multiples de 7 par tranches de 2.	>>>
Générale	Clé de divisibilité.	>>>
"	Congruence	>>>
Curiosité	35 et 53 + 3: divisibles par 7 (Propriété générale).	>>>

Propriétés des multiples de 7

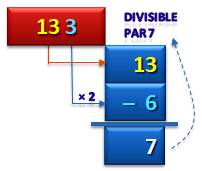
Observations

Construisons la table montrée ci-contre.

colonne 1: la suite des nombres de 1 à 20;

colonne 2: leur produit par 7;

colonne 3 et 4, les dizaines (d) et les unités (u); et

colonne 5: la différence entre les dizaines et deux fois les unités (sans le signe).

La colonne de droite produit 0, 7 ou 14, des multiples de 7.

Propriété

Pour les multiples de 7, les dizaines diminuées de deux fois les unités produisent un multiple de 7.

Si le nombre est noté 10d + u, en séparant son chiffre des unités, alors:

)

La barre verticale veut dire "divise"

Voir Divisibilité par les unités pour justification

Petit exercice …

Un nombre de trois chiffres peut s'écrire: N = 100c + 10d + u

Ou encore: N = 98c + 2c + 7d + 3d + u

En factorisant: N = 7 (14c + d) + 2c + 3d + u

Si N est divisible par 7: N = 7 (14c + d) + 2c + 3d + u = 7k

Ce qui implique que pour que N soit divisible par 7, il suffit que 2c + 3d + u soit divisible par 7.

Exemple avec 112: c = 1, d = 1 et u = 2; 2c + 3d + u = 7

et, effectivement: 112 = 7 x 16.

Pour les petits nombres
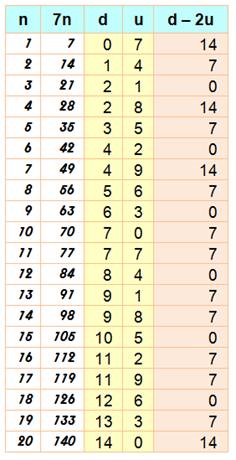
Méthode 1 Exploitation de la propriété exposée ci-dessus. Soustraire deux fois le dernier chiffre au nombre sans le dernier chiffre. Si ce nombre est divisible par 7, le nombre complet l'est également.
Le test peut se prolonger autant que nécessaire en utilisant le résultat.
Pourquoi ça marche?	Soit N un nombre formé de toutes ses dizaines (d) et de son unité (u): N = 10d + u. S'il est divisible par 7, alors: N = 10d + u = 7k. Prenons: 21u = 3 x 7u qui est divisible par 7 et retranchons à notre égalité: 10d + u – 21u = 7k' 10d – 20u = 7k' 10 (d – 2u) = 7k' Divisible par 7 que si d – 2u est divisible par 7. Voir Cas général

English corner

This method uses the fact that 7 divides 2x10 + 1 = 21. Start with the numeral for the number you want to test. Chop off the last digit, double it, and subtract that from the rest of the number. Continue this until you get a one-digit number. The result is 7, 0, or -7, if and only if the original number is a multiple of 7.

Pour les nombres de taille moyenne

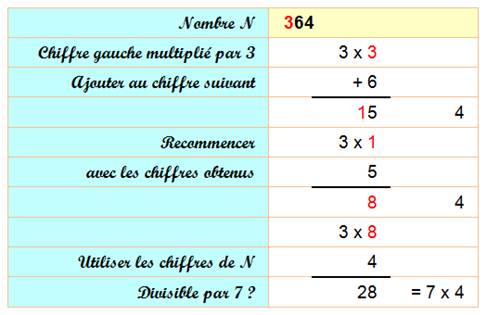
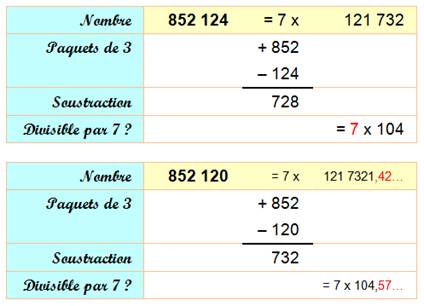
Méthode 2 - Principe

Ajouter trois fois le nombre de gauche au suivant.

Recommencer jusqu'à reconnaitre un nombre divisible par 7.

À droite est indiqué le nombre qui n'est pas encore exploité et qu'il faudra introduire dans le calcul. (Ici, dans la dernière opération).

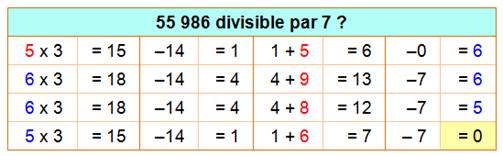
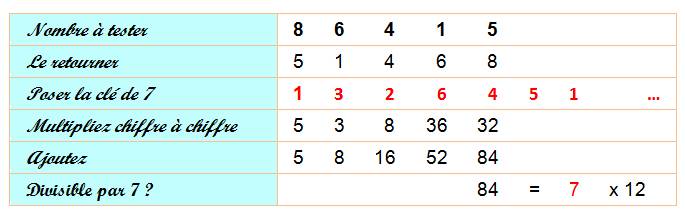
Voici le deux méthodes qui semblent les plus pratiques.

Méthode 2 (Sens )

Faire comme ci-dessus, mais à chaque opération soustraire le plus grand multiple de 7 possible, pour alléger le calcul.

Multipliez le chiffre de gauche (5) par 3.

Retirez 14 = 2x7, ce qui donne 1.

Lui ajoutez le chiffre suivant du nombre (5).

Le 6 obtenu est multiplié par 3. Etc.

Le 0 final indique que le nombre initial est divisible par 7.

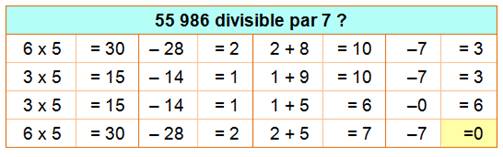
Méthode 2 bis (Sens )

Ajouter cinq fois le nombre de droite au précédent.

Recommencer jusqu'à reconnaitre un nombre divisible par 7.

Pour les grands nombres – Paquets de 3
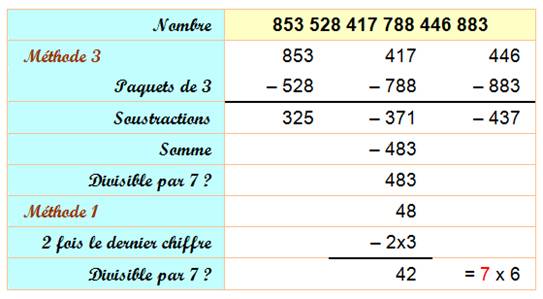
Méthode 3 Un nombre N est décomposé en paquets de trois chiffres à partir de la droite. On les soustrait. Si la différence est divisible par 7, alors le nombre original est divisible par 7.
Avec plusieurs paquets de 3 chiffres, additions et soustractions sont alternées. Bien respecter l'ordre des opérations et les signes. Astuce pour simplifier le calcul: remplacer 7 par 0, 8 par 1 et 9 par 2 au début du calcul et au fur et à mesure du calcul.	Note: 853 528 417 788 446 883 = 7 x 123456789 x 987654321

Voir Démonstration / Divisibilité par 13

Merci à Landri G. pour m'avoir alerté sur cette méthode

Exemple de calcul complet
Utilisation successive de la méthode 3 (grand nombre) et la méthode 1 pour finaliser sur un nombre à trois chiffres.

Pour les grands nombres – Paquets de 2 Algorithme de Gustavo Toja
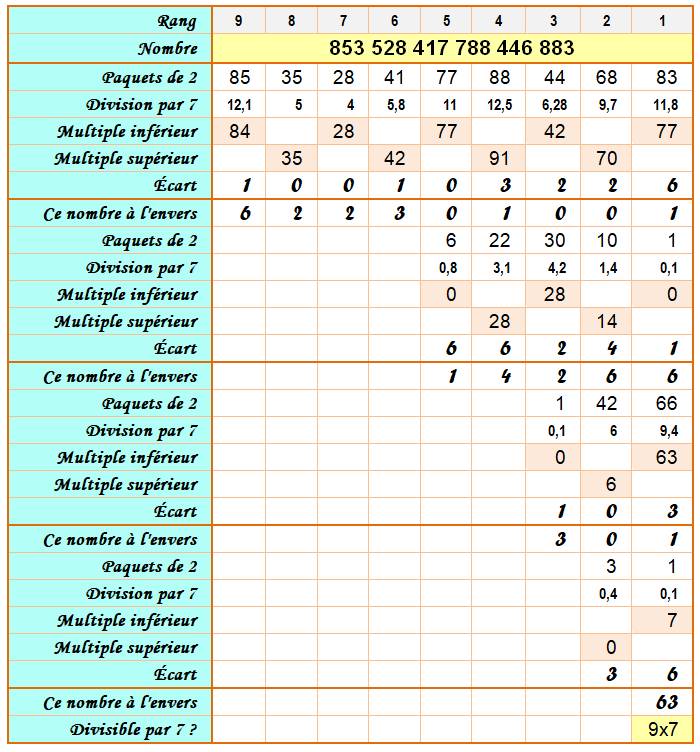
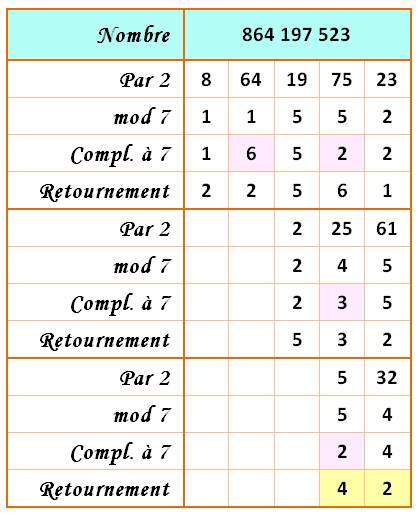
Méthode 4 Le nombre est découpé en paquets de 2 chiffres à partir de la droite. Les paquets de rangs impairs sont associés à un multiple de 7 inférieur et les pairs à un multiple de 7 supérieur. Les écarts sont calculés. Ils sont tous inférieurs à 7. Un nouveau nombre est formé en prenant les ces résultats dans l'ordre inverse. Remise en paquets de 2 et poursuite du procédé jusqu'à rencontrer un nombre divisible par 7, ou pas. La méthode est basée sur le fait que 1001 est divisible par 7. Et comme 1001 = 7 x 11 x 13, la méthode est aussi valable pour 11 et pour 13
Disposition pratique Le tableau montre une disposition permettant de poser le calcul plus rapidement que vu ci-dessus. Algorithme On regroupe toujours par paquet de 2 chiffres à partir de la droite; On calcule le reste de la division par 7 (mod 7). On prend le complément à 7 pour les nombres de rang pair (roses). On retourne le nombre; et; On recommence jusqu'à trouver un nombre divisible par 7 ou pas. Exemple Au rang 4, on trouve 64 Or 64 = 9 x 7 + 1, le reste est 1 (on dit que 64 = 1 mod 7) 64 est dans une colonne de rang pair, on prend le complément à 7: 7 – 1 = 6. Ce nombre, après inversion, se retrouve au rang 2.

Merci à Elie L. pour sa lecture attentive

Méthode général avec clé de divisibilité

Méthode de Pascal

Méthode 5

Le principe de cette méthode est exposé, d'une manière générale, en page:

clé de divisibilité

Si le nombre est très grand, répétez la clé autant que nécessaire.

La clé peut être aménagée pour éviter les grands nombres, mais en introduisant des nombres négatifs:

1 3 2 6 4 5 1 devient (avec des compléments à 7): 1 3 2 –1 –3 –2 1

Puissances 7 et divisibilité par 7			haut
Défi Montrer que cette expression est divisible par 7.
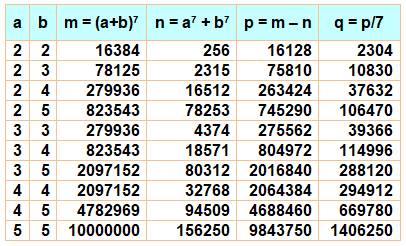
Observation Pour les valeurs de a et b de 2 à 5, la colonne de droite vérifie bine cette propriété. Comment la démontrer ? Piste On pense à développer (a + b)⁷ avec la formule du binôme. Sachant que 7 est un nombre premier et le PGCD des coefficients est égal à 7. Voir ce théorème.
Démonstration Généralisation Compte-tenu du théorème évoqué, cette propriété est vraie pour toute puissance p première:

Voir Coefficients du binôme / Développement du binôme / Nombre 7

FORME DIVISIBLE PAR 7
Théorème 7 f(n) = 3^{2n + 1} + 2^{n + 2} Valable pour les coefficients (en rose) prenant les valeurs: {1 et 2+3k}, {3 et 3+3k}, {5 et 1+3k}, {7 et 2+3k} … Note: aussi divisible par 11 pour {1 et 3+10k}, {2 et 1+10k} … si n est pair et pour {1 et 8+10k}, {2 et 6+10k} … si n est impair Démonstration par récurrence
Validation du point de départ
Valeur pour f(1). Le théorème est vrai pour n = 1.	f(1)	= 3³ + 2³ = 27 + 8 = 7 x 5
Validation de la récurrence
Supposons le théorème vrai pour n.	f(n)	= 7 . k
Calculons la valeur pour n+1. Sortons les puissances comme indiqué. On essaie de dégager des exposants identiques à ceux de f(n).	f(n+1)	= 3^{2(n+1) + 1} + 2^{(n+1) + 2} = 3^{2n + 3} + 2^{n + 3} = 9 . 3²ⁿ⁺¹ + 2 . 2ⁿ⁺²
Calculons la différence indiquée.	f(n+1) – 2 f(n)	= 9 . 3²ⁿ⁺¹ + 2 . 2ⁿ⁺² - 2 . 3²ⁿ⁺¹ - 2 . 2ⁿ⁺² = 7 . 3²ⁿ⁺¹
La différence est divisible par 7. L'un des termes de la différence est divisible par 7 (notre hypothèse). L'autre terme doit l'être aussi pour assurer la divisibilité de la différence.	f(n) f(n+1)	= 7 . k = 7 . h
Conclusion
Si la propriété est vraie pour une valeur (n), elle est vraie pour la valeur suivante (n + 1). Or elle est vérifiée pour n = 1. Elle est vraie pour tous les nombres suivants.

Devinette – Solution

Est-ce que 421 435 est divisible par 7 ?

421 435 =	420 000	+ 1 400	+ 35
Divisé par 7	60 000	+ 200	+ 5
421 435 / 7 =	60 205

Retour / Autres énigmes

Suite	Divisibilité par 7 – Suite (encore des surprises …) Méthode générale par congruence Divisibilité par 8 Divisibilité – Index
Voir	Calcul mental – Index Formes polynomiales Géométrie – Index Nombres abondants Nombres parfaits Théorie des nombres – Index
DicoNombre	Nombre 7 Nombre 3 367
Site	Divisibility by 7, 11 and 13 – Alexander Bogomolny
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi7.htm